Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Изучение математики в школе начинается с изучения небольшой области чисел, которая постепенно расширяется, и вводятся новые понятия. Знакомство с числами учащиеся начинают с натуральных чисел, позже вводятся отрицательные числа и нуль. Решение простейших практических задач, в которых требуется провести измерения, не обходится без введения понятия дробного числа. Иррациональные числа могут быть введены как длина диагонали квадрата со стороной 1, не являющаяся рациональным числом. Для решения простейших квадратных уравнений с натуральными коэффициентами действительных чисел становится недостаточно, используем новые числа, которые сначала назывались мнимыми, а затем комплексными, для них квадратный корень из отрицательного числа имеет смысл.

Разделом «Комплексные числа» во многих учебно-методических комплексах завершается основная образовательная программа по предмету «Алгебра и начала математического анализа» в 10-11 классах. Выделим основные причины такого подхода: во-первых, комплексные числа показывают связь алгебры, геометрии и тригонометрии; во-вторых, дают возможность увидеть структуру изученных числовых множеств и операций с этими множествами, открывают возможность в решении широкого класса задач алгебраического и геометрического содержания. Кроме того, решение большого количества задач техники и физики сводится к решению квадратного уравнения, у которого отрицательный дискриминант. Такие уравнения не имеют решения на множестве действительных чисел, но, несмотря на это, их решение имеет физический смысл.

Комплексные числа пока не входят в контрольно-измерительные материалы ЕГЭ по математике, но их включение не исключено. Такие задания проходят апробацию и представлены ФИПИ в перспективной модели на 2022 год по математике профильного уровня, есть большая вероятность, что такие задания появятся на ЕГЭ в ближайшие годы. Целью работы является описание возможностей улучшить формирование предметных результатов по теме комплексные числа в курсе алгебры и геометрии.

Материалы и методы исследования

Для проведения исследования использовались теоретические методы: сравнительно-сопоставительный анализ учебно-методических комплексов по алгебре и началам математического анализа для 10 и 11 классов [1-3], учебных пособий по алгебре для педагогических вузов [4; 5], анализ педагогического опыта в процессе работы со студентами первого курса педагогического вуза в рамках преподавания дисциплин «Вводный курс математики» и «Алгебра», темы «Комплексные числа».

Результаты исследования и их обсуждение

Выполненный анализ позволяет сделать вывод о близком содержании темы «Комплексные числа» в пособиях [1-3]. Набор заданий ограничивается стандартными вычислениями в алгебраической и тригонометрической форме, решении линейных и квадратных уравнений. Наибольший интерес, и в то же время трудность, представляют задачи, связанные с геометрическим изображением комплексных чисел. Изучение темы в конце 11 класса сопряжено с сокращением и без того небольшого количества часов, так как часто необходимо уделить время повторению и подготовке к итоговым экзаменам. Поэтому, сталкиваясь с этой темой в университете, студенты испытывают трудности. Обучающимся в классах физико-математического и технологического профилей для лучшего в дальнейшем усвоения и понимания данного материала можно было бы начать освещать данную тему раньше, чем в 11 классе.

Например, после изучения свойства степени учеников можно познакомить с возведением в степень мнимой единицы. После знакомства с законами сложения векторов стоит рассказать о сложении комплексных чисел по правилу параллелограмма, а также о том, что каждое комплексное число можно задать с помощью радиус-вектора на плоскости, соединив начало координат и точку (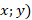, соответствующую комплексному числу .

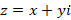Для школьников и студентов большой интерес будут представлять задания, выполняемые с использованием электронных образовательных ресурсов. Одной из программ, позволяющих работать с комплексными числами, является математическая динамическая среда GeoGebra. В работах [6; 7] рассмотрено применение GeoGebra в исследовательской деятельности бакалавров по математическим дисциплинам. Школьникам можно предложить построить в GeoGebra радиус-векторы, соответствующие комплексным числам, найти их длины. Покажем пример построения радиус-векторов, соответствующих комплексным числам 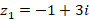и 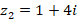, а также использования команды «Вектор(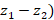» для получения разности двух векторов 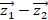(рис. 1).

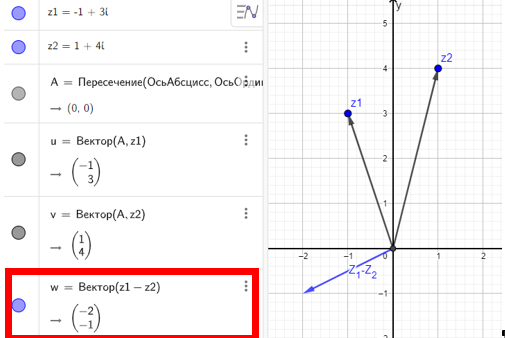
Рис. 1. Радиус-векторы на плоскости в GeoGebra

Комплексный метод решения планиметрических задач является наименее распространенным, и в школе он совсем не рассматривается. Сопоставление точки 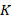с координатами 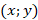и комплексного числа 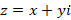будем считать комплексной координатой точки 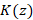. Число 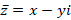назовем комплексно-сопряженным с 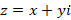. При таком подходе можно доказать формулы, используемые в дальнейшем при решении геометрических задач 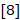, например:

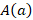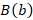1. Для точек и число 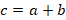будет являться координатой точки 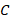, такой, что 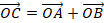. Число 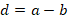будет координатой для точки 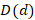, где выполняется .

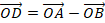2. Формула для нахождения площади положительно ориентированного треугольника

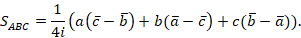
3. Общее уравнение окружности в комплексных координатах c центром 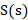и радиусом 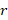имеет вид: 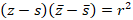, если центр окружности находится в начале координат, то уравнение окружности определяется следующим образом: .

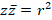4. Два отрезка 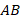и 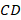ортогональны тогда и только тогда, когда число 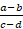является чисто мнимым.

5. Формула для отыскания комплексной координаты точки 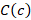, делящей отрезок 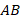(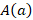, 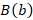) в заданном отношении(

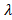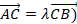
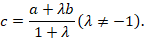
6. Формула для нахождения расстояния между двумя точкам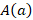и и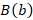

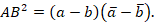
Покажем использование этого подхода при решении геометрических задач.

Задача 1. В прямоугольном треугольнике 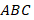с прямым углом 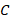проведена медиан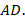а Точка 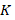принадлежит данной медиане, и известно, что 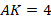. Найдите площадь треугольника 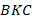, если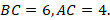

Решение: из треугольника 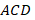по теореме Пифагора найдем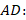

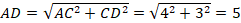. Тогда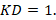

Введем прямоугольную систему координат, в которой прямая

Библиографическая ссылка