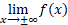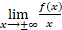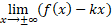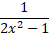Самостоятельная работа обучающихся является важнейшей составной частью образовательной программы высшего образования. Объем, формы и виды самостоятельной работы обучающихся определяются учебным планом и рабочей программой учебной дисциплины [1, 2].
Учебная дисциплина «Математический анализ» является обязательной дисциплиной, которая реализуется на первом курсе в первом и втором семестрах для обучающихся по направлению подготовки 38.03.01 Экономика.
Согласно образовательному стандарту РАНХиГС учебная дисциплина «Математический анализ» обеспечивает формирование следующей общепрофессиональной компетенции ПКо ОС II – 1 Способен использовать методы математического анализа для решения прикладных задач [3]. При этом минимальным объемом результатов обучения дисциплине является знание теоретических основ методов дифференциального и интегрального исчисления функции одной и нескольких переменных, основ теории рядов; умение решать задачи дифференциального и интегрального исчисления для решения прикладных задач и применять ряды для решения прикладных задач. Учебная дисциплина «Математический анализ» составляет 10 зачетных единиц, т.е. 360 академических часов. На контактную работу с преподавателем выделено 128 академических часов, из них 64 академических часа на проведение занятий лекционного типа и 64 академических часа на проведение практических занятий; на самостоятельную работу обучающихся выделено 156 академических часов для обучающихся очной формы обучения. Таким образом, видно, что практически половина времени, отведенного на изучение учебной дисциплины, приходится на самостоятельную работу обучающихся.
Цель исследования – описание подходов к организации самостоятельной работы обучающихся на практических занятиях по учебной дисциплине «Математический анализ».
Материалы и методы исследования
Материалы исследования: федеральный государственный образовательный стандарт высшего образования и образовательный стандарт РАНХиГС по направлению подготовки 38.03.01 Экономика, Положение об организации самостоятельной работы студентов РАНХиГС, рабочая программа дисциплины «Математический анализ», результаты промежуточной аттестации обучающихся, личные разработки автора для проведения практических занятий. Методы исследования: теоретические (анализ педагогической литературы, анализ нормативных документов) и эмпирические (наблюдение, анализ учебной документации).
Результаты исследования и их обсуждение
Очень часто даже на этапе завершения образования обучающиеся не обладают навыками организации и выполнения самостоятельной работы. Практически отсутствует навык работы с литературой, недостаточно развито умение анализировать имеющуюся информацию, выделять ключевые моменты, делать собственные выводы. Поэтому уже начиная с первого курса необходимо уделять особое внимание вопросам организации самостоятельной работы обучающихся. Вместе с тем решение данной задачи усугубляется спецификой самой учебной дисциплины «Математический анализ», освоение которой предполагает наличие у обучающихся математического мышления. В результате освоения учебной дисциплины обучающийся должен уметь применять методы математического анализа при решении профессионально-ориентированных задач. Поэтому математическая подготовка в профессиональном образовании будущего специалиста в экономической области является базовой потребностью и рассматривается как необходимый компонент процесса формирования профессиональной компетентности экономиста. На основе вышесказанного важную роль играет организация самостоятельной работы обучающихся, как мотивационная составляющая успешного освоения дисциплины. Основными формами организации самостоятельной работы обучающихся являются: аудиторная самостоятельная работа и внеаудиторная самостоятельная работа [2]. Обратимся непосредственно к самому понятию самостоятельной работы.
Исследования, посвященные понятию самостоятельной работы обучающихся, ее методам и формам организации, занимают в отечественной педагогической теории и практике одно из важнейших мест. Данное понятие рассматривается как средство обучения; метод обучения; организационная форма обучения; средство вовлечения обучающихся в учебную деятельность (Ю.К. Бабанский [4], П.И. Пидкасистый [5], Т.И. Шамова [6]), форма организации образовательного процесса, стимулирующая активность, самостоятельность, познавательный интерес обучающихся [7]. Таким образом, на основе анализа педагогической литературы по данной тематике можно сделать вывод о том, что нет единого подхода к трактовке и статусу понятия самостоятельной работы. Оно включает в себя познавательную деятельность, которую выполняют обучающиеся как при проведении внеаудиторной самостоятельной работы, так и при проведении аудиторной самостоятельной работы. О самостоятельной работе обучающихся можно говорить как о некотором целенаправленном процессе, в котором предполагается учебно-познавательная деятельность самих обучающихся во всех организационных формах проведения учебных занятий, а также и во вне этих занятий, то есть во внеаудиторное время, когда обучающиеся самостоятельно знакомятся и изучают необходимый учебный материал, а также – это вся совокупность тех учебных заданий, которые должен выполнить обучающийся в процессе обучения в образовательной организации высшего образования. Существуют и другие подходы к понятию самостоятельной работы, когда она рассматривается как учебная деятельность обучающегося без непосредственного участия и помощи со стороны преподавателя. В этом случае при выполнении учебных заданий основная роль отводится самому обучающемуся, его самостоятельности, но характер предметной и мыслительной деятельности при этом остается вне поля зрения преподавателя. Учитывая вышесказанное, можно сделать вывод о том, что при проведении самостоятельной работы обучающиеся сталкиваются с определенными трудностями, среди которых можно выделить следующие: поиск учебного материала, который необходим для самостоятельного изучения отдельных тем и вопросов, работа с содержанием учебной литературы, классификация и систематизация теоретического материала, изложенного в различных источниках, определение взаимосвязи и взаимозависимости между ними, методология учебной дисциплины, практико-ориентированность полученных знаний. Не представляется возможным выделить какой-либо преобладающий характер трудностей, возникающих у обучающихся при проведении самостоятельной работы. Все они носят комплексный характер, и здесь особая роль отводится преподавателю, который должен организовать и направить самостоятельную работу обучающихся для решения поставленных задач. Поэтому умение организовать, управлять и осуществлять контроль самостоятельной работы обучающихся – одна из наиболее важных и вместе с тем сложных задач в деятельности преподавателя. Необходимо развивать у обучающихся навыки самостоятельной работы в освоении содержания учебной дисциплины, формировать самостоятельность мышления, стремление к саморазвитию и самосовершенствованию.
Приведем несколько примеров организации самостоятельной работы обучающихся на практических занятиях по учебной дисциплине «Математический анализ». Так для лучшего понимания методологической составляющей дисциплины можно использовать практические задания тестового характера (как открытого, так и закрытого типов), иллюстрирующие понятия, определения и теоремы дисциплины. Если есть возможность, то можно представлять геометрическую интерпретацию различных математических фактов, что способствует более эффективному усвоению изучаемого учебного материала. Рассмотрим несколько таких заданий по теме «Исследование свойств функций и построение их графиков».
Задание 1. На рисунке функция y = f(x) задана своим графиком (рис. 1). Найти промежуток убывания функции.
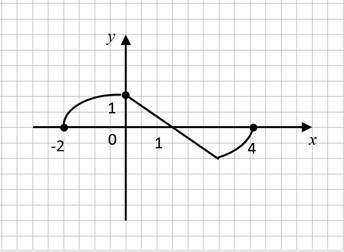
Рис. 1. График функции y = f(x)
Варианты ответов:
1. 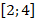 ; 2.
; 2. 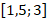 ; 3. (0;3); 4.
; 3. (0;3); 4. 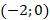 .
.
Задание 2. На рисунке представлены графики функций (рис. 2). Укажите график четной функции.
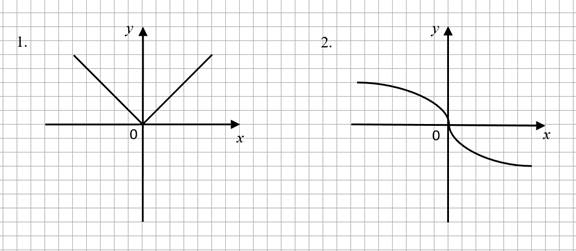
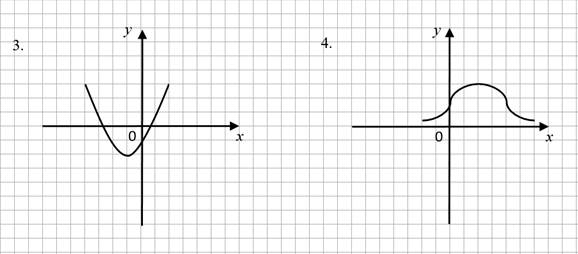
Рис. 2. Графики функций
Задание 3. График производной функции 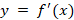 , заданной на отрезке
, заданной на отрезке 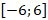 , изображен на рисунке (рис. 3). Укажите количество промежутков возрастания и убывания функции y = f(x).
, изображен на рисунке (рис. 3). Укажите количество промежутков возрастания и убывания функции y = f(x).
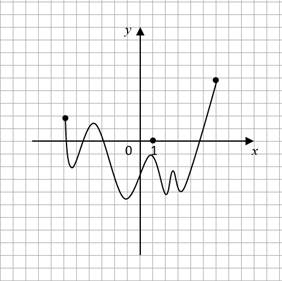
Рис. 3. График производной функции 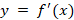
Задание 4. Укажите, какие асимптоты имеет график функции y = f(x), изображенной на рисунке (рис. 4).
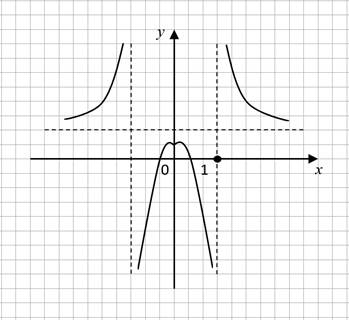
Рис. 4. График функции y = f(x)
Варианты ответов:
1. х = 1 и х = -1 – вертикальные асимптоты;
2. х = 1 – вертикальная асимптота, у = 2/3 – горизонтальная асимптота;
3. у = 2/3 – наклонная асимптота;
4. х = 1 и х = -1 – вертикальные асимптоты; у = 2/3 – горизонтальная асимптота.
Следует отметить, что также надо делать акцент не только на зрительную идентификацию тех или иных понятий, определений и теоретических фактов, но и отрабатывать умения по аналитическому представлению данных воспроизводить их графическое изображение, то есть решать и обратные задачи.
Задание 5. Даны свойства функции. Схематически построить ее график.
1. 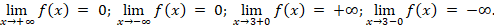
2. 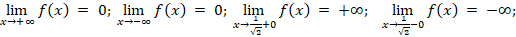
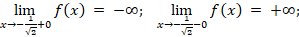 (0, -1) – точка максимума.
(0, -1) – точка максимума.
3. 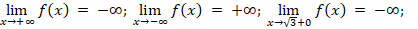
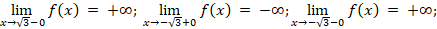
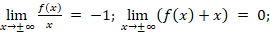 (0; 0) – точка перегиба.
(0; 0) – точка перегиба.
Активная аудиторная самостоятельная работа возможна лишь при условии устойчивой мотивации. Главным фактором устойчивой мотивации является подготовка обучающегося к будущей профессиональной деятельности. В соответствии с образовательным стандартом РАНХиГС изучение учебной дисциплины «Математический анализ» должно быть направлено не только на освоение собственно методов математического анализа, но и на формирование умений решать профессионально-ориентированные задачи. Для формирования способности использовать методы математического анализа для решения прикладных задач можно предложить следующие практические задания.
Задание 6 (кейс-задание). Дана функция 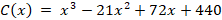 , где C (у.е.) – издержки производства, x (ед.) – объем выпускаемой продукции.
, где C (у.е.) – издержки производства, x (ед.) – объем выпускаемой продукции.
1. Пусть 9 ед. – начальный объем производства. До какого значения должен вырасти объем производства, чтобы при этом издержки производства монотонно убывали?
Варианты ответов:
а) 15,0; б) 10,0; в) 16,5; г) 14,5.
2. Если значения х принадлежат отрезку 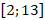 , то наибольшие издержки производства равны…
, то наибольшие издержки производства равны…
3. Если выручка от реализации одной ед. продукции равна 33 у.е., то прибыль будет максимальной при х, равном…
Задание 7. Дана функция 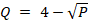 , где Q – суточный спрос на минеральную воду (тыс. шт.), P – за одну бутылку (руб.). Формула имеет эффективную область работы от 1 до 9 руб. Какова должна быть цена за одну бутылку минеральной воды, чтобы при этом совокупная выручка была максимальной?
, где Q – суточный спрос на минеральную воду (тыс. шт.), P – за одну бутылку (руб.). Формула имеет эффективную область работы от 1 до 9 руб. Какова должна быть цена за одну бутылку минеральной воды, чтобы при этом совокупная выручка была максимальной?
При отработке практических навыков при изучении темы «Исследование свойств функций и построение их графиков» также полезными могут оказаться практические задания, направленные не только на констатацию полученного результата, но и отражающие аналитические рассуждения, которые проводил обучающийся при решении конкретной задачи. С одной стороны, это позволит заставить обучающегося осознанно применить соответствующую формулу или теорему и осуществить осмысленный выбор пути решения задачи, а с другой стороны, даст возможность преподавателю на этапе контроля отследить, с какими трудностями столкнулся обучающийся при решении задачи. Это позволит преподавателю провести доскональный анализ затруднений, которые возникли у обучающегося и спланировать дальнейшую работу по их устранению.
Задание 8. Найти асимптоты графика функции и схематично построить ее график. Предварительно заполнить следующую таблицу (таблица).
Нахождение асимптот графика функции
|
f(x) |
D(f) |
Предполагаемые точки разрыва |
Односторонние пределы |
Значение |
Значение |
Значение |
|
|
|
|
|
|
|
|
Данный подход к организации самостоятельной работы обучающихся на практических занятиях был использован в процессе освоения учебной дисциплины «Математический анализ» обучающимися первого курса по направлению подготовки 38.03.01 Экономика Дальневосточного института управления – филиала РАНХиГС и показал положительную динамику с точки зрения успеваемости и качества освоения учебной дисциплины, о чем свидетельствуют результаты промежуточной аттестации обучающихся. Так, в 2020–2021 учебном году успеваемость составила 75 %, а качество – 61 %; в 2021–2022 учебном году успеваемость – 88 %, качество – 71 %.
Заключение
Таким образом, предложенный подход к организации аудиторной самостоятельной работы обучающихся на практических занятиях по учебной дисциплине «Математический анализ» способствует качественному освоению учебного материала, повышению интереса к самостоятельной работе и формированию профессиональной компетентности будущего экономиста.
Библиографическая ссылка
Жидкова М.И. НЕКОТОРЫЕ ПОДХОДЫ К ОРГАНИЗАЦИИ АУДИТОРНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ОБУЧАЮЩИХСЯ ПО ДИСЦИПЛИНЕ «МАТЕМАТИЧЕСКИЙ АНАЛИЗ» // Современные проблемы науки и образования. 2022. № 5. ;URL: https://science-education.ru/ru/article/view?id=32103 (дата обращения: 10.02.2026).
DOI: https://doi.org/10.17513/spno.32103