Современный подход к кинообразованию носит практико-ориентированный характер, подготовка будущего инженера в сфере кинематографии требует умения решать широкий спектр прикладных задач, умения работать и с реальными объектами, и с моделями или макетами в условиях киносъемки.
В большинстве стандартных задач по физике учащимся даётся готовая физическая модель, причём зачастую идеализированная: материальная точка, невесомая и нерастяжимая нить, абсолютно твёрдое тело, идеальный газ, идеальный вольтметр и т.п. Такие задачи учащиеся неплохо умеют решать ещё со школы – осуществлению перехода от физической модели к математической и её решению в школе уделяется достаточно времени. Однако будущему инженеру придётся столкнуться с совсем другими, настоящими, а отнюдь не идеализированными объектами, зачастую с неполными данными.
Переход от реальных объектов к физическим моделям требует специфических навыков, таких как системное мышление, «умение видеть за деревьями лес и за лесом деревья» - умение одновременно представлять объект как единое целое и в деталях, понимание поведения объекта целиком и взаимодействия его составляющих, умение идеализировать объект, выделяя его существенные свойства и абстрагируясь от несущественных... Указанный переход от объекта к модели всегда требует значительного числа допущений и упрощений. Чтобы научиться грамотно составлять физические модели, студенты должны уметь выбирать главные, наиболее подходящие для цели исследования свойства реального объекта, делать грамотные оценки свойств объектов, пользоваться дополнительными источниками информации. Только тогда они научатся составлять физические модели, адекватные исследуемым объектам [1].
Цель исследования – развитие теории и методики решения задач с видеоконтентом в медиаобразовании и совершенствование методической системы обучения физике в профессиональной подготовке киноинженеров.
Материалы и методы исследования
Методологией научной работы является компетентностный подход в медиаобразовании, задачный подход в теории и методике обучения физике, методы демонстрационных примеров, методы учебного физического эксперимента, а также феноменологический подход в моделировании реальных физических процессов и систем с использованием информационных и коммуникационных технологий. В работе использовалась учебная медиатека, современная видеоаппаратура кино и телевидения и собственный макет маятника Фуко.
В теоретической подготовке киноинженера необходимо отметить иерархию законов, в которой важные в прикладных задачах законы сохранения следуют из той или иной симметрии пространства-времени. Симметрия пространства и времени неразрывно связана с фундаментальными законами сохранения: закон сохранения энергии вытекает из однородности времени, закон сохранения импульса следует из однородности пространства, закон сохранения момента импульса выводится из изотропности пространства.
Данная связь для консервативных систем выводится из теоремы, доказанной Эмми Нётер в 1918 году. Теорема Нётер показала природу законов сохранения, связанную с инвариантностью уравнений движения при тех или иных преобразованиях координат и времени. К таким преобразованиям относится так называемое масштабное преобразование, при котором координаты и время увеличиваются или уменьшаются в определенное число раз: 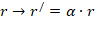 ,
, 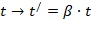 , где α, β – некоторые масштабные множители. Очевидно, что при постоянной массе кинетическая энергия преобразуется
, где α, β – некоторые масштабные множители. Очевидно, что при постоянной массе кинетическая энергия преобразуется 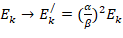 [2, с. 205].
[2, с. 205].
Преобразование потенциальной и полной энергии зависит от координат и позволяет находить связь пространственных и временных характеристик движения без обращения к законам динамики, потому что преобразование энергии можно рассматривать при изменении самой физической системы, считая единицы измерения прежними. Наивысшим проявлением симметрии пространства-времени является принцип относительности - эквивалентность инерциальных систем отсчета. Переход между уровнями методологических принципов, законов сохранения и частных законов и теорий показывает уровень нашего понимания окружающего мира.
Заметим, что в методике решения задач учет симметрии и масштабные преобразования существенно упрощают алгоритм, основанный на «принципе относительности» для актуальных задач кинематографа. В данном случае рассматривается реальная сцена (система координат 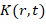 и экран воспроизведения видеофильма (система координат
и экран воспроизведения видеофильма (система координат 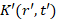 ), т.е. «инерциальные системы отсчета». Возможна постановка двух типов задач. Первая задача: по известному времени съемки и времени воспроизведения видеоконтента определение частоты кадров. Вторая задача: по известным параметрам изображения на экране и частоте съемки восстановление параметров сцены, например траектории движения тела.
), т.е. «инерциальные системы отсчета». Возможна постановка двух типов задач. Первая задача: по известному времени съемки и времени воспроизведения видеоконтента определение частоты кадров. Вторая задача: по известным параметрам изображения на экране и частоте съемки восстановление параметров сцены, например траектории движения тела.
Результаты исследования и их обсуждение
В качестве примера рассмотрим задачу первого типа, в которой, на первый взгляд, ничего не дано. В социальной сети представлено видео [3] красивого прыжка рыси (рис. 1). Очевидно, что это видео было снято в технике slow mo, то есть съёмка осуществлялась при большей частоте кадров, и при нормальной демонстрации возникает эффект «замедления времени», что позволяет рассмотреть прыжок во всех деталях. Никаких метаданных в видео нет. Требуется оценить, на какой частоте производилась съёмка. Данные задачи: время прыжка (время съемки) - 0,75 с, время прыжка на видео - 30 с при стандартной частоте 25 FPS (Frames Per Second – кадров в секунду). Решение: из масштабных преобразований для «инерциальных систем отсчета» следует, что видео было замедленно в β=40 раз, то есть частота съёмки 1000 FPS.

Рис. 1. Кадр из видео «Прыжок рыси»
В задачах второго типа используется феноменология моделей физических процессов и систем в разных приближениях теории. В демонстрационной динамической задаче возможно рассмотрение наиболее простой модели свободного падения, учитывая симметрию траектории движения тела.
На первый взгляд, даже не ясно, как приступать к этой задаче, поскольку в явном виде не дано ничего. Но эта задача вполне решаема.
Однако можно заметить, что дело происходит на Земле, то есть нам, как минимум, известно ускорение свободного падения. Рысь, конечно, совсем не материальная точка, но обнаружить её центр масс – точку, относительно которой она поворачивается в полёте, несложно при покадровом просмотре. Пропорции рыси на видео вполне естественны, то есть соотношение ширины и высоты кадра не изменялось. Это означает, что угол вектора начальной скорости можно брать непосредственно с видео, опять же при покадровом просмотре. Для оценки масштабных коэффициентов воспользуемся сайтом «Кошачьи» [4], согласно которому взрослая рысь обыкновенная имеет в среднем длину ~ 1 м. Исходя из этого, оцениваем длину прыжка рыси и максимальную высоту прыжка по центру масс, начальную скорость и время прыжка (время съёмки) ~ 0,75 с.
Теперь у нас в рассмотрении типовая задача по механике о свободном падении тела под углом к горизонту с симметричной параболической траекторией, параметры которой можно связать соотношением подобия с частотой съёмки. Заметим, что усложнение задачи, связанное с учетом реальных факторов, например сопротивления среды, приводит к дифференциальным динамическим уравнениям и численным алгоритмам решения.

Рис. 2. Симметрия при масштабных преобразованиях кадра
Рассмотрим ещё одну задачу по физике в области кинематографии, с которой операторы сталкиваются на практике: кинооператор снимает сцену взрыва на уменьшенной модели. Как следует изменить частоту кадров при съемке, чтобы в кинофильме сцена выглядела правдоподобно? Из соображений симметрии следует, что чем меньше объект, тем выше должна быть скорость съёмки. Именно так поступают операторы при съёмке фильмов на миниатюрных макетах объектов [5, с. 25], что до сих пор широко применяется в кинематографе даже в эпоху компьютерной графики и дизайна.
Видеозадачники по физике и задачи с видеоконтентом уже существуют и достаточно широко используются в медиаобразовании [6]. Особенно эффективно они могут применяться и в дистанционном обучении, и в учебном физическом эксперименте.
Ускоренную видеозапись (режим slow mo, который сейчас есть в большинстве смартфонов) зачастую целесообразно использовать и в физическом эксперименте, особенно при работе с быстрыми процессами. Например, в классической лабораторной работе по проверке закона сохранения импульса при столкновении шаров применённая по инициативе студентов ускоренная видеозапись позволила измерять отклонения шаров с большей точностью (рис. 3).

Рис. 3. Кадр видеозаписи лабораторной работы по механике, выполненной студентами в режиме slow mo
Когда в 2017 г. в Санкт-Петербургском государственном институте кино и телевидения был изготовлен макет маятника Фуко (рис. 4), ускоренная видеосъёмка позволила не только демонстрировать вращение Земли, но и проводить прецизионные измерения в лабораторном практикуме по физике [7].



Рис. 4. Демонстрационный эксперимент с маятником Фуко в СПбГИКиТ
Опыты с маятником Фуко являются существенным прогрессом в механике, астрономии и натурфилософии Коперника и Кеплера, Галилея и Ньютона, Кориолиса и самого Фуко.
Совместными усилиями преподавателей и студентов в СПбГИКиТ был изготовлен маятник Фуко, один из самых больших в Европе (длина нити 27 м, масса 60 кг), дающий возможность выполнять прецизионные измерения при исследовании фундаментальных законов механики [7]. Следует отметить, что размер и масса маятника Фуко имеют принципиальное значение для повышения точности измерений в проводимых экспериментах. Главная проблема в демонстрациях маятника Фуко - это затухание колебаний. При большей массе и длине нити затухание колебаний происходит значительно медленнее, а колебания маятника значительно точнее описываются гармонической функцией.
Для решения этой проблемы часто применялись автоколебания под действием высокочастотного электромагнитного поля. Различные режимы возбуждения колебаний в подобного рода колебательных системах подробно изучаются в прикладных задачах численного моделирования физических процессов [8]. При этом на угловую скорость вращения маятника оказывает влияние соотношение различных параметров осциллятора.
Лабораторная конструкция маятника Фуко - это нетривиальная техническая задача, нуждающаяся в оригинальных инженерных решениях. В сущности, как доказывают результаты вычислительного эксперимента, согласованием различных параметров осциллятора возможно решить проблему затухания колебаний выходом на предельный цикл фазовой траектории. Автоколебательный режим при этом поддерживается электродинамическими пондеромоторными силами, воздействующими на массивный металлический шар.
Заключение
Впервые в практике медиаобразования предложена методика решения физических задач с видеоконтентом на основе методологических принципов симметрии, подобия и относительности. Разработан цикл физических задач для инерциальных систем отсчета типа «сцена - экран», позволяющий изучать возможные режимы видеосъемки в современных технологиях цифрового кинематографа и макетирования. Также впервые в теории и методике обучения физике исследованы вопросы прецизионных измерений в учебном физическом эксперименте с использованием собственных макетов, видеоаппаратуры и медиатеки видеозаписей.
Предложенный новый интегративный подход, сочетающий классические методы и дидактические принципы в методике обучения физике с современными технологиями кино и телевидения, позволит решить проблему формирования профессиональных компетенций будущего инженера в системе кинообразования.
Полученные научные результаты могут быть успешно применены в инновационных педагогических разработках в области медиаобразования, методики решения задач и учебного физического эксперимента для научной специальности 13.00.02 «Теория и методика обучения физике», а также для направлений подготовки 44.03.01 «Физическое образование», 11.03.01 «Радиотехника» (профиль «Аудиовизуальная техника») и 55.05.03 «Кинооператорство» в СПбГИКиТ.
Библиографическая ссылка
Ходанович А.И., Штейн Б.М., Кондыбаева И.Ш. СОВЕРШЕНСТВОВАНИЕ МЕТОДИЧЕСКОЙ СИСТЕМЫ ОБУЧЕНИЯ ФИЗИКЕ В ПРОФЕССИОНАЛЬНОЙ ПОДГОТОВКЕ КИНОИНЖЕНЕРОВ // Современные проблемы науки и образования. 2022. № 3. ;URL: https://science-education.ru/ru/article/view?id=31835 (дата обращения: 16.02.2026).
DOI: https://doi.org/10.17513/spno.31835



