Цели и задачи подготовки российскими университетами специалистов для зарубежных стран определены документом «Основные положения Концепции государственной политики Российской Федерации в области подготовки национальных кадров для зарубежных стран в российских образовательных учреждениях» (18.10.2002). Именно с этого времени начинает свою работу в Казанском национальном технологическом университете факультет международных образовательных программ.
Любая область науки и технологии в современном мире достаточно широко использует различные математические термины и понятия. Приемы линейной и векторной алгебры применяются при описании динамики физических, технологических и экономических процессов, для представления и обсуждения результатов исследований. С разделов «Линейная алгебра» и «Векторная алгебра» начинается изучение дисциплины «Высшая математика» по направлениям «Химическая технология», «Биотехнология» Казанского национального исследовательского университета. Овладение иностранными студентами алгеброй – первого из изучаемых разделов математики – сопряжено с наибольшими трудностями.
Значительная часть слушателей подготовительного отделения факультета международных образовательных программ КНИТУ – будущие студенты вузов технологического направления. Следует отметить, что иностранные студенты – в основном выходцы из стран Азии (дальнее зарубежье) и Африки – владеют материалом школьного курса математики на достаточно хорошем уровне; кроме того, изучение математики на подготовительном отделении начинается во втором семестре, т.е. тогда, когда студенты уже приобрели некоторые навыки использования русского языка. При работе на факультете довузовской подготовки возникает необходимость переработки и дополнения содержания учебного материала с опорой на анализ имеющихся у обучаемых базовых компетенций по элементарной математике и знаний в русском языке. Приходится учитывать и их культурную составляющую. Соединение математики и русского языка способствует созданию информационно-образовательной среды, комфортной для каждого обучающегося и применения на практике усвоенного материала.
Следует отметить достаточное количество учебного материала по математике для иностранных студентов. Как правило, целью большинства существующих пособий является повторение элементов курса элементарной математики, необходимых для последующего обучения в вузе [1]. Мы же предлагаем преподавание математики для слушателей подготовительного отделения факультета международных образовательных программ КНИТУ с элементами разделов первого семестра вузовской программы. Это более полезный формат, нежели только повторение школьной программы.
Цель нашей работы: провести адаптацию содержания учебного материала по математике для слушателей подготовительного отделения факультета международных образовательных программ КНИТУ с элементами разделов первого семестра вузовской программы; подготовить учебно-методический материал по курсу математики для работы с иностранными студентами, отвечающий требованиям стандарта высшего образования и смежных учебных дисциплин.
Проанализировав степень математической подготовки иностранных студентов и имеющиеся у них навыки самостоятельной работы, мы пришли к пониманию необходимости внесения корректировки в организацию учебного процесса и адаптацию существующего учебно-методического обеспечения.
Объект нашего исследования – процесс формирования необходимых математических компетенций у слушателей подготовительного отделения факультета международных образовательных программ КНИТУ.
Предмет исследования – обучение математике по направлениям «Химическая технология» и «Биотехнология» студентов подготовительного отделения факультета международных образовательных программ КНИТУ.
Задачи исследования:
– выявить особенности обучения математике иностранных студентов направлений «Химическая технология» и «Биотехнология» на подготовительном отделении факультета международных образовательных программ;
– с учетом выявленных особенностей провести адаптацию содержания курса математики по разделам «Числовые выражения», «Линейная алгебра» и «Векторная алгебра»;
– разработать систему заданий и упражнений на формирование математических понятий.
Используемые методы исследования: общенаучные методы исследования, такие как анализ, систематизация, обобщение; эмпирические методы: наблюдение, сбор материала, опрос, педагогический эксперимент.
Многие обозначения в математике являются общеупотребимыми и понятны на многих языках мира. Приезжающие студенты имеют различные уровни знаний по элементарной математике, особенности культурного поведения, что приходится учитывать в учебном процессе.
При подготовке материала учебного пособия для иностранных студентов мы полагали, что разработка должна решать задачу освоения разделов математики, а также элементов русского языка [2]. В пособие мы включили список слов и терминов, языковых конструкций, типичных в коммуникации между преподавателем и студентами на аудиторных занятиях. Ключевые слова и словосочетания, знание которых необходимо для усвоения данной темы, даются двух языках: русском и английском. Учтены требования к стандартизации и унификации используемой терминологии и обозначений. Пособие, кроме краткого содержания материала, включает пропедевтические и послетекстовые упражнения на русском языке, задания для закрепления материала. Цель этих упражнений – помочь в усвоении необходимой математической терминологии, повторить и восполнить знания и навыки в области математики. После изучения теоретического материала полезно использовать задания, учитывающие индивидуальный уровень знания математики каждого студента.
Для закрепления изученных ранее терминов, понятий, свойств, определений в пособии предложены вопросы для проверки уровня усвоения материала и типовые задания для самостоятельного решения с ответами.
Программа по математике для подготовительных отделений вузов включает базовый материал курса элементарной математики и высшей математики. Подготовленное учебно-методическое пособие содержит три раздела: «Числовые выражения», «Линейная алгебра», «Векторная алгебра», адаптированные для усвоения иностранными студентами. В каждом разделе представлены необходимый теоретический материал, математические тексты для активизации лексического запаса студентов, тесты на проверку целостности полученных знаний. Материал пособия представлен в компактной форме. Для облегчения усвоения теория сопровождается практическими заданиями с решениями и комментариями на русском языке, для наиболее часто используемых терминов представлена их запись на английском языке. Сочетание знаково-цифрового и лексического материала на первых занятиях позволяет скоординировать обучение математике и русскому языку.
Основные математические понятия и термины, используемые в пособии, иллюстрируются на примерах. Рассматриваются упражнения, направленные на отработку математической лексики, получение и закрепление необходимых вычислительных навыков.
Рабочая программа по дисциплине «Математика» для подготовительных отделений вузов составлена с учетом приказа Министерства образования и науки РФ № 1304 (3.10. 2014). Общее количество часов, выделенное на изучение математики, – 254. На практические занятия по разделу «Основные математические символы и операции» отводится 16 часов, по разделу «Элементы линейной и векторной алгебры» – 27. Безусловно, прежде чем перейти к алгебраической тематике, необходимо повторить используемые в дальнейшем арифметические действия, работу с дробями, возведение в целую положительную степень n, извлечение корня n-ой степени. Данным темам в пособии отводится первая глава «Числовые выражения». Большая часть заданий здесь – чтение математических выражений или их запись, например:
– записать в виде выражения: а) квадрат суммы чисел х и один; б) три плюс восемь разделить на минус семь плюс шесть; в) корень квадратный из девяти плюс шесть в квадрате;
– прочитать и вычислить: а) 23 − 32; б) 2) 50 −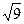 
; в)
;
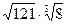– среди перечисленных выражений выделить выражения, принимающие положительные значения: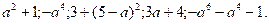 
С методом Крамера, применяемым для решения систем, иностранные студенты знакомы по школьной программе, знают они и способы вычисления определителей до третьего порядка включительно. Поэтому на занятиях по линейной алгебре (12 часов практических занятий) основное внимание уделяется методу Гаусса и матричному способу решения систем. Для проверки усвоения основных понятий предлагаются тестовые задания с вариантами ответов, например:
– что произойдет с определителем при следующей перестановке его строк: первую строку поменяем местами со второй, вторую строку – с третьей, а третью строку – с первой? Варианты ответов: 1) не изменится; 2) изменит свой знак; 3) увеличится втрое; 4) уменьшится втрое;
– метод Крамера для решения систем уравнений не используется, если: 1) матрица системы − квадратная; 2) определитель системы отличен от нуля; 3) определитель системы равен нулю; 4) число неизвестных и число уравнений системы совпадают;
– если при преобразовании расширенной матрицы системы получена матрица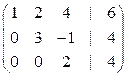 
, тогда: 1) у системы единственное решение; 2) бесконечное множество решений; 3) у системы нет решений; 4) имеет только нулевое решение.
Фрагмент изучения векторной алгебры (15 часов практических занятий) продемонстрируем на примере знакомства с темой «Скалярное произведение».
1. Иностранные студенты подготовительного отделения, в основном владея английской грамматикой на достаточно высоком уровне, неплохо ориентируются и в математической терминологии. Поэтому для лучшего усвоения терминов по данной теме основные словосочетания предлагаются и на английском языке. Например:
– скалярное произведение векторов – scalar product of vectors;
– сумма произведений соответствующих координат – sum of the products of the corresponding coordinates;
– косинус угла между векторами – cosine of the angle between vectors;
– скалярное произведение коммутативно – properties of the scalar product;
– скалярное произведение двух ненулевых векторов равно нулю – scalar product of two non – zero vectors equals zero, и т.д.
2. Дается краткий теоретический обзор изучаемого материала: определение, свойства, приложения скалярного произведения – в аналитической и словесной формах:
– 
. 
= 
, 
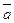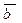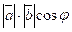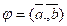− скалярное произведение векторов 
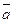и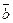 
равно модуль вектора 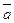умножить на модуль вектора
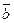умножить на косинус угла между векторам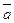и и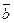
;
– векторы 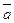и 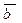перпендикулярны (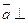 
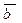) (`а и 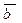ненулевые), если их скалярное произведение равно нулю: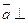 
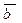
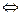
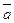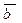. = 0.
3. Задачи с подробным решением:
Чему равна работа Е силы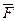 
={2;−1;−4}, если точка ее приложения, двигаясь прямолинейно, перемещается из точки А (1;−2;3) в точку В (5; −6; 1)?
Решение. Применим формулу работы: Е = .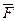
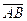. Определим координаты вектора 
: =
= 
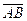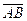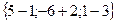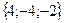. Так как известны координаты векторов и 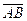, для вычисления скалярного используем координатную форму записи:
Е=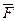.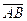=2∙4+(−1)∙(−4)+(−4)∙(−2)=20.
4. Задачи и упражнения для самостоятельной работы.
5. Вопросы для проверки усвоения основных понятий с вариантами ответов.
Например:
– координаты векторов увеличили в два раза. Как изменится их скалярное произведение?
1) увеличится в четыре раза; 2) увеличится в два раза; 3) не изменится; 4) увеличится на четыре;
– скалярное произведение двух ненулевых векторов будет равно нулю тогда и только тогда, когда векторы: 1) перпендикулярны; 2) коллинеарные; 3) компланарны; 4) единичные;
– метод Крамера решения систем уравнений не используется, если: 1) число уравнений системы меньше числа ее неизвестных; 2) определитель системы равен нулю; 3) определитель системы больше нуля; 4) свободные члены системы уравнений равны нулю.
Подобные задания достаточно информативны: требуются понимание сути вопроса, знание терминов, правильное решение.
Использование для проверки усвоения основных понятий вопросов в такой форме особенно актуально в нынешнее время, когда в условиях пандемии многие учащиеся подготовительного отделения занимаются дистанционно [3]. В условиях частично дистанционного обучения успех применения технологии перевернутого обучения для организации учебного процесса с использованием цифровых технологий во многом определяется уровнем мотивации студентов и методами организации учебного процесса преподавателем [4].
Для иностранных студентов технологического направления вузов (будущих студентов – химиков) очень полезно обсуждение заданий профессионально-прикладного характера (параллельно с математикой на подготовительном отделении изучается и химия). Применение уже известных математических знаний при решении подобных задач помогает учащимся получить математические навыки, необходимые в их будущей деятельности [5].
Примером может послужить следующее задание.
Рассматриваются химические реакции, происходящие в реакторе:
СО + 2Н2 
СН3ОН
2СО + 4Н2 СН3ОСН3 + Н2О
2СН3ОН СН3ОСН3 + Н2О
4СО + 8Н2 С4Н9ОН + 3Н2О.
Требуется: 1) составить стехиометрическую матрицу; 2) определить число независимых реакций и независимые реакции; 3) записать уравнения суммарных независимых реакций образования ключевых продуктов.
Решение. Обозначим: А1 = СО, А2 = Н2, А3 = СН3ОН, А4 = СН3ОСН3, А5 = Н2О, А6 = С4Н9ОН. В новых обозначениях реакции будут иметь вид системы уравнений:
–А1 – 2А2 +А3 = 0
–2А1 – 4А2 + А4 +А5 = 0
–2А3 + А4 +А5 = 0
– 4А1 – 8А2 + 3А5 +А6 = 0.
Запишем стехиометрическую матрицу и определим ее ранг:
~ 
~ 
.
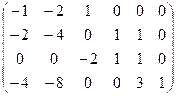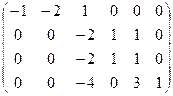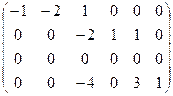При вычислении ранга матрицы были проведены преобразования: первую строку сначала умножаем на (−2) и прибавляем ко второй, затем первую строку умножаем на (−4) и прибавляем к четвертой. Далее из второй строки вычитаем третью. Ранг стехиометрической матрицы равен 3. Это говорит о том, что в этой системе есть три независимые реакции.
Стехиометрические коэффициенты соответствуют этим трем суммарным реакциям:
–А1 – 2А2 +А3 = 0
–2А3 +А4 +А5 = 0
–4А3 + 3А5 +А6 = 0.
Или
СО + 2Н2 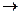СН3ОН
2СН3ОН 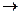СН3ОСН3 + Н2О
4СН3ОН 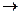3Н2О + С4Н9ОН.
Третья реакция исходной системы является линейно зависимой.
Достижению наилучшего результата в освоении студентами математики способствует закрепление пройденного материала. С этой целью в учебном пособии предложены вопросы для проверки уровня усвоения основных понятий и типовые задания для самостоятельного решения с ответами.
Успешность занятий по математике во многом определяется и личностью преподавателя, его компетентностью и заинтересованностью в учебном процессе. Преподаватель должен уметь вызывать интерес к учению, потребность в знаниях.
Проведена реорганизация учебного процесса на основе предложенного методического обеспечения. Сформирован набор дидактических материалов по темам курса: «Числовые выражения», «Линейная алгебра», «Векторная алгебра». Подготовлено учебное пособие с опорой на проведенный анализ специфики обучения иностранных студентов. Данное учебное пособие, созданное для методического обеспечения обучения математике студентов-иностранцев, способствует быстрому и надежному вхождению в разделы дисциплины «Математика» высших учебных заведений.
Библиографическая ссылка
Хузиахметова Р.Н., Дегтярева О.М. АДАПТИРОВАННЫЙ КУРС ОБУЧЕНИЯ МАТЕМАТИКЕ ИНОСТРАННЫХ СТУДЕНТОВ // Современные проблемы науки и образования. – 2022. – № 1. ;URL: https://science-education.ru/ru/article/view?id=31391 (дата обращения: 19.04.2024).