В 2018 году в национальном проекте «Образование» была поставлена задача создания к 2024 году современной безопасной цифровой образовательной среды. В системе высшего профессионального образования возникла проблема: как обеспечить необходимый уровень математической и информационной подготовки преподавателей, способных подготовить специалистов, удовлетворяющих потребностям современной науки, экономики, промышленности. Более того, в условиях сокращения количества аудиторных часов, выделяемых на изучение математики, при классическом формате обучения достаточно сложно передать студенту объем знаний, необходимых для использования в будущей профессиональной деятельности, а также сформировать у него компетенции, определенные государственными стандартами высшего образования.
Объектом нашего исследования является формирование математической компетентности студентов Казанского национального исследовательского технологического университета в процессе профессиональной подготовки. Предмет исследования: содержание и организация процесса формирования профессиональных компетенций студентов с учетом междисциплинарной интеграции в условиях цифровизации образования. Цель исследования: совершенствование учебно-методического обеспечения для реализации компетентностного подхода при изучении математики, конструирование учебного процесса с использованием современных цифровых технологий. Задачи исследования: определить условия цифровизации образования в аспекте формирования математической компетентности студентов, выявить междисциплинарные связи математики с дисциплинами профессиональной подготовки как основу построения курса, создать базу профессионально направленных задач. Формируемые компетенции требуют качественного знания предмета, умения использовать методы математики для анализа профессиональных задач [1]. Как одну из возможностей решения этих проблем можно предложить часть изучаемого материала выносить на самостоятельное изучение. При этом его объем и состав должны зависеть как от специализации студентов, объема выделяемых часов на изучение предмета, так и уровня математической подготовки студентов, их способностей к самостоятельной работе, умения использовать цифровые технологии. Преподаватель математики сталкивается с проблемами недостаточной мотивации студентов, низкого уровня их математической подготовки, неумения самостоятельно работать и находить нужную информацию. Поэтому актуальной является задача разработки нового методического обеспечения курса математики (корректировки существующего методического обеспечения), позволяющего успешно решить эти задачи.
Применяемые методы исследования: анализ методической литературы, содержания федеральных государственных стандартов, личное преподавание, наблюдение, изучение и анализ деятельности учащихся, тестирование, сравнительный анализ экспериментальных данных.
Как показывает практика, для подготовки специалиста, способного к самостоятельному творческому мышлению, необходимо эффективнее использовать деятельностный подход в процессе обучения. Деятельностный подход требует включения в курс математики решения профессионально ориентированных и прикладных задач, использования различных прикладных пакетов программ для решения подобных задач, графической иллюстрации, проведения анализа и сравнения полученных решений. Важно научить студентов различным способам проверки полученных решений и приучить их проводить контроль и корректировку своей деятельности на различных этапах, приучить к интерпретации и анализу полученных результатов. Необходимо, чтобы студенты были знакомы с различными существующими методами решения задач и умели выбирать из них наилучшие и наиболее эффективные, знать критерии отбора. Нужно научить их умению комбинировать различные методы решения, анализировать исходные данные, определять, что дано, что надо найти, видеть связь между исходными данными и выбираемым методом решения. Надо, чтобы студент в любой нематематической задаче смог найти математическую составляющую, построить математическую модель исследуемых процессов. Перечисленные задачи требуют перехода от описательного к качественному деятельностному подходу в изучении математики. Перед преподавателем встает задача реорганизации учебного процесса и, как следствие, создания более разветвленной системы учебных пособий. Учебник нужно дополнить задачником, содержащим, кроме основных классических примеров и задач, материал, расширяющий и углубляющий содержание курса математики, а также помогающий студентам организовать самостоятельную работу. Необходимо обновить систему отбора содержания учебных пособий. Содержание обучения должно включать как системообразующие знания, так и показывать области применения этих знаний, перспективы и ограничения применения математических методов и моделей [2]. Для повышения мотивации изучения математики студентами, что важно в условиях увеличения количества часов на самостоятельную работу и уменьшения аудиторной нагрузки, желательно проводить параллели с развитием математического знания и развитием научно-технического прогресса. Обучение должно сочетать принципы фундаментальности и профессиональности, отвечать требованиям непрерывности образования, преемственности, системности и перспективности [3]. Математическая подготовка должна включать как формальное, так и практическое содержание. Необходимым условием эффективности достижения целей высшего профессионального образования является интеграция математических и инженерных дисциплин. Стратегия интеграции дисциплин позволяет исключить излишнюю формализацию предмета математики. Для сужения объема содержания по математике следует руководствоваться соображениями соответствия объема изучаемого материала отведенному времени на его изучение, минимальной достаточности материала и наименьшей сложности его изложения для восприятия студентами.
В основе решения многих инженерных задач лежат математические методы и модели, поэтому важно усилить акцент на формирование прикладной математической компетентности студентов, что невозможно без отслеживания существующих связей между математической и профессиональной подготовкой студентов. Формирование прикладной математической компетентности студентов может быть реализовано, если в обучении использовать обсуждение и решение заданий, имеющих междисциплинарный и прикладной характер, то есть включая в курс прикладные и профессионально ориентированные системы задач. Для формирования системы таких заданий нужно определить существующие общие профессиональные проблемы по специальностям одного направления [4]. Подборку задач для математической подготовки студентов нужно дополнить такими, для решения которых могут эффективно применяться цифровые средства (платформы-калькуляторы, прикладные пакеты), примерами, где находятся численные или (и) аналитические решения, задачами, где требуется найти аналитическое и графическое решения, а также заданиями, сопровождаемыми визуализацией полученной аналитической информации. Для обеспечения выполнения соответствия объема курса математики отведенному времени на изучение дисциплины к отбору прикладных задач должны быть предъявлены определенные требования: математическое решение не должно занимать большой промежуток по времени, задача должна иметь практическую важность, должна быть ясно сформулирована и опираться на ранее изученные факты и понятия. Для профессионально ориентированных заданий разумно выделить следующие моменты: они должны решать проблему из профессиональной деятельности специалиста, для описания параметров и характеристик исследуемого объекта или явления можно применить изученный ранее или изучаемый математический аппарат, решение такой задачи должно помогать студенту усвоить те или иные математические знания и навыки, необходимые в его профессиональной деятельности.
Перечисленным выше требованиям вполне удовлетворяет задача, предлагаемая студентам первого курса направления «Химическая технология»:
В реакторе протекают следующие реакции:
2СН4 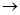 С2Н2 +3Н2
С2Н2 +3Н2
СН4 + О2 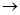 СО + Н2 + Н2О
СО + Н2 + Н2О
2СН4 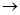 С2Н4 + 2Н2
С2Н4 + 2Н2
С2Н4 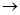 С2Н2 + Н2
С2Н2 + Н2
СН4 + 0,5 О2 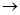 С2Н2 + Н2О
С2Н2 + Н2О
Н2 + 0,5 О2 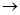 Н2 О
Н2 О
С2Н2 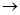 2С + Н2.
2С + Н2.
Требуется: 1) составить стехиометрическую матрицу; 2) определить число независимых реакций, выбрать независимые реакции и ключевые вещества; 3) записать уравнения суммарных независимых реакций образования ключевых продуктов.
Решение. Введем обозначения: А1 = С2Н2, А2 = СО, А3 = Н2О, А4 = С2Н4, А5 = С, А6 = СН4, А7 = О2, А8 = Н2. В буквенном виде система химических реакций приобретает вид:
2А6 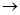 А1 +3А8
А1 +3А8
А6 + А7 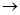 А2 + А8 + А3
А2 + А8 + А3
2А6 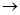 А4 +2А8
А4 +2А8
А4 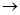 А1 +А8
А1 +А8
А4 + 0,5А7 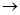 А1 + А3
А1 + А3
А8 + 0,5А7 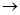 А3
А3
А1 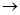 2А5 + А8.
2А5 + А8.
Составим стехиометрическую матрицу и вычислим ее ранг: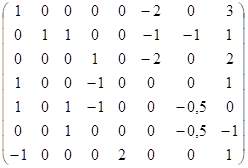 ~
~ 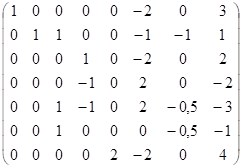 ~
~
~ 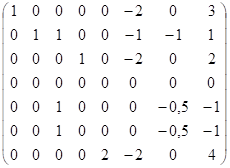 ~
~ 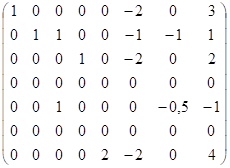 ~
~
~ 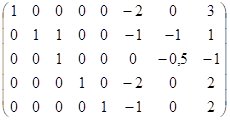 .
.
Первую строку, умноженную на (−1), прибавили к четвертой и пятой, затем сложили третью строку с четвертой, пятую с шестой. Пятую строку, умноженную на (−1), прибавили к шестой. Ранг стехиометрической матрицы равен 5, т.е. в этой системе имеется пять независимых реакций. Стехиометрические коэффициенты соответствуют этим пяти суммарным реакциям:
2А6 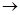 А1 + 3А8
А1 + 3А8
А6 + А7 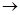 А2 + А3 + А8
А2 + А3 + А8
0,5А7 + А8 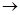 А3
А3
2А6 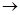 А4 + 2А8
А4 + 2А8
А6 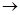 А5 + 2А8 .
А5 + 2А8 .
Или
2СН4 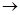 С2Н2 + 3Н2
С2Н2 + 3Н2
СН4 + О2 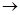 СО + Н2О + Н2
СО + Н2О + Н2
0,5О2 + Н2 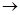 Н2О
Н2О
2СН4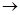 С2Н4 + 2Н2
С2Н4 + 2Н2
СН4 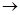 С + 2Н2 с пятью ключевыми веществами С2Н2, СО, Н2О, С2Н4, С.
С + 2Н2 с пятью ключевыми веществами С2Н2, СО, Н2О, С2Н4, С.
Не меньший интерес у студентов вызывает и следующая задача.
В результате проведения эксперимента нужно приготовить смесь из m различных веществ. Смесь должна содержать bi единиц i-го вещества (i = 1,2,…,m). Известно, что для приготовления смеси имеетcя n компонентов, каждый из которых (j-й) содержит aij единиц i-го вещества (j = 1,2,…,n).
Обозначим 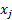 количество j-го компонента, которое необходимо взять для приготовления смеси. Математическая модель задачи нахождения количества каждой компоненты будет представлять систему линейных алгебраических уравнений вида:
количество j-го компонента, которое необходимо взять для приготовления смеси. Математическая модель задачи нахождения количества каждой компоненты будет представлять систему линейных алгебраических уравнений вида: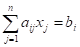 , (i=
, (i=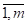 ).
).
Пример. Требуется приготовить 4250 кг нитрующей смеси из трех компонент: 22% воды (b1), 16% азотной кислоты (b2), 62% серной кислоты (b3) из смеси: Н2О – 5% (a11), HNO3 – 85% (a21), H2SO4 – 10% (a31); из олеума: Н2О – 0% (a12), HNO3 – 0% (a22), H2SO4 – 104% (a32); из отработанной кислоты: Н2О – 30% (a13), HNO3 – 0% (a23), H2SO4 –70% (a33). Определить расход кислот, идущих на приготовление этой смеси.
Решение. Составим математическую модель задачи.
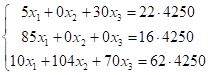
Решив систему методом Крамера, получим количество каждой из компонент, входящих в заданную смесь: x1 = 800 кг, х2 =467 кг, х3 = 2983 кг.
Подобные задачи имеют практическую значимость для студентов младших курсов при изучении раздела «Линейная алгебра».
Важно отметить, что в вузе параллельно с математикой студенты изучают ряд других дисциплин, в том числе и специальных, в которых востребованы знания и умения, приобретаемые при изучении математики. Дополнение курса математики серьезными профессиональными задачами проблематично ввиду асинхронности курсов математики и изучаемых специальных дисциплин. Ввиду этого важно прослеживать и выстраивать последовательность и объем материала при изучении математики в соответствии с востребованностью соответствующих методов, приемов и понятий математики при изучении специальных дисциплин.
Преподавателями выпускающих кафедр КНИТУ была отмечена важность математических методов при изучении их предметов и высказаны пожелания как о некотором изменении наполнения курса математики, так об изменении последовательности изложения материала. При анализе программ дисциплин, изучаемых в нашем университете, для которых имеют практическую значимость методы математики, были внесены коррективы в наполнение содержания курса математики и некоторые изменения в последовательность изложения материала, с целью обеспечения преемственности изучения и полноты содержания предмета.
Выход на качественный уровень усвоения студентами предмета высшей математики в условиях сокращения аудиторных часов невозможен без интенсификации процесса обучения. Для интенсификации процесса изучения математики и реализации деятельностного подхода в обучении удобно использовать онлайн-калькуляторы, такие как pocketteacher.ru, matrixcalc.org, allcalc.ru, прикладные пакеты, например Mathcad. Электронная платформа Cocal позволяет по-новому организовать деятельность по изучению математических понятий и объектов. Важное место среди цифровых технологий занимает база знаний и вычислительных алгоритмов WolframAlpha.
Применение информационных технологий требует изменения не только наполнения курса математики, но и технологий обучения. В условиях необходимости проведения частично дистанционного обучения преподавателями кафедры высшей математики КНИТУ применяется технология «перевернутый класс» как один из видов интерактивного обучения [5]. Студентам предлагается самостоятельно просмотреть и законспектировать онлайн-лекции (заранее разработанные и записанные преподавателем), разобрать вне аудитории некоторый теоретический материал, ответить на предложенные вопросы, принять участие в онлайн-дискуссиях и обсуждениях материала, изучить дополнительные интернет-источники (во внеаудиторное время). Затем на практических занятиях совместно с преподавателем изученный материал обсуждается и применяется для выполнения практических заданий. В процессе перевернутого обучения вместе с учебной деятельностью используются и образовательные технологии. Как мы могли увидеть, преимущества перевернутой формы обучения заключаются в том, что студенты могут осваивать теоретический материал в индивидуальном режиме, преподаватель располагает большим временем для объяснения затруднительных моментов, традиционное домашнее задание возможно выполнять в аудитории при поддержке преподавателя. Реализация такой формы обучения, по крайней мере на первых порах, требует дополнительных временных затрат от преподавателя, умения использовать цифровые технологии. При реализации перевернутого обучения преподаватель должен спроецировать систему учебных задач, разработать и записать соответствующий лекционный материал, сопроводив его для удобства текстовой версией.
Формирование прикладной математической компетентности студентов успешно реализуется, если в обучении использовать систему профессионально ориентированных задач. Сформулированы задания для реализации деятельностного подхода в обучении. Проведена реорганизация учебного процесса на основе разработанного методического обеспечения. Для интенсификации процесса изучения математики и реализации деятельностного подхода в обучении удобно использовать онлайн-калькуляторы и прикладные пакеты, электронные платформы. Использование технологии перевернутого обучения при переходе в 2020 году на дистанционное обучение (требуемое в условиях пандемии) привело авторов к следующим выводам: успех перевернутого обучения во многом зависит от синергии между преподавателем и студентом, требует постоянной мотивации студентов, более активного применения информационных технологий. Значительно увеличивается роль учебных материалов и самообучения, а также роль личности педагога. Запуск такой формы обучения сопряжен с большими временными затратами преподавателя.
Библиографическая ссылка
Дегтярева О.М., Хузиахметова Р.Н. РЕАЛИЗАЦИЯ КОМПЕТЕНТНОСТНОГО ПОДХОДА ПРИ ИЗУЧЕНИИ МАТЕМАТИКИ В КОНТЕКСТЕ ЦИФРОВИЗАЦИИ ВЫСШЕГО ОБРАЗОВАНИЯ // Современные проблемы науки и образования. 2021. № 6. ;URL: https://science-education.ru/ru/article/view?id=31275 (дата обращения: 11.02.2026).
DOI: https://doi.org/10.17513/spno.31275



