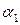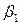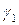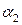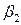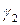В условиях цифровизации всех сфер современной жизни применение методов обучения автоматизированному анализу различных закономерностей в природе и обществе является необходимым условием качественной подготовки обучающихся в самых разных отраслях знаний как естественно-научного, так и социально-экономического направлений. Это предопределено тем фактом, что аналитическое исследование функций, описывающих указанные закономерности, является зачастую излишне затратным для исследователя как по времени, так и по интеллектуальным усилиям, а в некоторых случаях необходимо рассматривать такое огромное количество всевозможных вариантов и комбинаций параметров, что человеку данная задача становится не под силу, тем самым снижается эффективность принимаемых им решений. В этих случаях, очевидно, и целесообразно применение численных методов и алгоритмов анализа функций и компьютерной обработки соответствующей информации. Хотя численные методы не всегда дают верные ответы на возникающие у исследователя вопросы (в силу, например, возможного накопления компьютером ошибок округления), но они помогают реализовать необходимые исследовательские действия в течение долей секунды там, где человеку для получения решения задачи пришлось бы потратить несопоставимо больше времени без их применения. Кроме того, точности графоаналитических методов, как правило, с запасом хватает для анализа многих прикладных задач.
Материалы и методы исследования
Наиболее эффективным для анализа математических функций с целью общности исследования и скорейшего выявления их свойств является метод задания их коэффициентов, показателей степеней и оснований, фаз, амплитуд и других характеристик в параметрическом виде. Любая функциональная зависимость может быть задана в виде уравнения: F(x,y,…,t,…;a,b,…)=0, где x,y,…,t,… – множество переменных аргументов, a,b,… – множество параметрических аргументов функции F. В качестве F рассматриваются элементарные математические функции – степенные (многочлены, рациональные, иррациональные), тригонометрические, показательные и логарифмические, а также их комбинации (сложные функции), когда эти характеристики задаются в виде параметров. Отметим, что под параметром понимается такой математический объект, который обладает одновременно свойством классических переменных величин принимать любое допустимое числовое значение и свойством констант иметь фиксированное числовое значение. Например, в выражении для квадратного трехчлена ax2+bx+c символы a, b, с – параметры, x – переменная, 2 – константа. Под параметрическим анализом задачи будем понимать полный или частичный анализ рассматриваемых в ней функций, соотношений и их взаимодействия с точки зрения перебора допустимых значений параметров и получения критических точек (корней, экстремумов, разрывов, порогов) и интервалов (диапазонов изменения) функций.
Исследования прикладных задач, описывающих реальные объекты и процессы в виде математических формул, имеют глубокую историю и широчайший круг областей знаний, в которых эти исследования осуществляются. Однако история применения численных методов компьютерного анализа едва преодолела половину века. В настоящее время существует значительное количество зарекомендовавших себя на рынке математических пакетов, обзор которых приведен, например, в [1; 2]: Derive, Mathematica, MathCad, MATLAB, Maple и многие другие. При решении широкого круга математических задач (начиная от анализа функций и решения математических соотношений и их систем, заканчивая решением дифференциальных, интегральных, матричных, вариационных, статистических задач, включая оптимизационные и другие классы) каждый из указанных программных комплексов имеет свои преимущества и недостатки. К некоторым из существенных, на наш взгляд, недостатков перечисленных комплексов относится неудобство, невысокая эффективность или даже отсутствие полноценных возможностей решения задач многопараметрического анализа функций. В этой связи целью данной статьи является описание возможностей программного комплекса [3] (далее графического анализатора, графоанализатора), предназначенного для параметрического анализа нескольких функций с несколькими параметрами, в том числе общими для функций, в режиме реального времени, со скоростью до нескольких десятков перебираемых значений параметра в секунду. Указанный комплекс обладает набором возможностей для исследования параметрических соотношений, заданных в R2 в следующих формах: 1) y=f(x); 2) x=f(y); 3) в однопараметрической форме x=x(t), y=y(t) с параметром t; 4) в полярной системе координат r=r(φ), где φ – угол между горизонтальной осью и исходящим из начала отсчета радиус-вектором длины r; 5) в виде неравенств f(x)~g(x), где символ «~» соответствует одному из четырех знаков неравенства; 6) в табличном виде. К основным отличительным свойствам комплекса относятся возможности автоматического распознавания переменных и использования практически не ограниченного количества параметров, их изменение в ручном и автоматическом режимах. Кроме того, он позволяет находить корни и точки пересечения функций, уравнения касательных, вычислять определенные интегралы, исследовать системы уравнений и неравенств с общими параметрами на общем графическом поле, решать другие полезные для математического анализа функций задачи. Пакет также обладает ключевым преимуществом других графических пакетов, заключающимся в возможности приближенного определения корней алгебраических соотношений, которые невозможно или затратно получать аналитически (например, когда необходимо найти корни полинома степени выше 2-й или в соотношении одновременно присутствуют функции разных классов – степенная, показательная, логарифмическая, тригонометрическая и т.п.). Программный комплекс содержит такие инструменты работы с графиками, изображениями и результатами анализа, как: 1) масштабирование и перемещение координатной плоскости; 2) сохранение конфигураций графика в файл с возможностью последующей загрузки; 3) скриншот и сохранение числовой аналитической информации; 4) гибкая настройка интерфейса (изменение вида координатной плоскости, цветов, способа отображения и другое) отдельно для каждого документа; 5) проверка синтаксиса формул при их вводе и многие другие стандартные возможности компьютерной обработки. Основными достоинствами графического анализатора состоят в том, что он позволяет оперативно визуализировать и динамически анализировать изучаемые объекты и процессы путем построения и многопараметрического исследования функций, имеет программный интерфейс, интуитивно понятный для освоения обучающимися образовательных организаций основного, профессионального и высшего образования.
Суть концепции и идеи системного использования графоанализатора для решения различных прикладных задач изложена в работе [4] достаточно давно, однако его применение оставалось на уровне учреждений среднего образования для решения, как правило, учебных задач естественно-научного цикла, и результаты соответствующих исследований широко опубликованы не были. Активное использование пакета в учреждениях высшего образования началось в середине 2010-х годов с применения его в экономико-математических моделях, в том числе при решении оптимизационных задач. Следует отметить, что наилучший эффект при анализе прикладных задач достигается в случае возможности комбинирования численно-графических и аналитических методов их решения. В этой связи с помощью комплекса [3] далее производятся анализ и классификация такого класса сложных функций, как дробно-квадратичная функция (ДКФ), которая имеет широкие приложения в различных областях знаний, с одной стороны, и допускает как аналитические, так и численные методы исследования – с другой.
Результаты исследования и их обсуждение
Рассмотрим дробно-квадратичную функцию, представленную в общем параметрическом виде: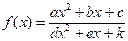 
. В своих частных проявлениях данная функция имеет широчайший круг приложений. Например, при d=e=0 
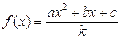является обычной параболой (многочленом второй степени), широко применяемой в математике за счет возможности ее полного исследования элементарными методами. При a=d=0 
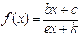представляет собой дробно-линейную функцию, используемую в различных приложениях математики в биологии, физике, экономике, в том числе при решении задач оптимизации, а при a=c=d=0 
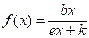можно подобрать значения оставшихся параметров, при которых она достаточно точно, в некоторой локальной области, описывает логистическую кривую Q(x)=K/(1+С*eD/x), используемую в экономической теории для описания, например, связи между доходом и спросом экономических агентов. Описание некоторых свойств ДКФ можно найти в статье [5], а также на электронном ресурсе [6]. Вместе с тем в указанных источниках отсутствуют примеры практического применения ДКФ при анализе прикладных задач. В других же литературных источниках информация о ДКФ не выходит за рамки исследования функций значениями с конкретными коэффициентами или графических иллюстраций с однопараметрическим анализом.
Начнем классификацию ДКФ, исходя из наличия у нее наклонных асимптот. Пусть коэффициенты a и d одновременно не равны нулю, причем многочлены в числителе и знаменателе не пропорциональны и не имеют общих корней, то есть дробь несократима на линейный множитель. Тогда все такие функции можно разделить на две группы: 1)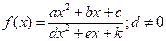 
; 2)
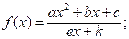d=0; e≠0. Далее общность свойств ДКФ в обеих группах определим наличием сингулярностей функции в точках, в которых ее знаменатели принимают нулевые значения, что регулируется знаком дискриминанта D=e2–4dk, а также наличием корня линейной функции в знаменателе 2). В этой связи все ДКФ первой группы можно разделить на три подгруппы, ставя в основу деления условия: 1) D>0; 2) D=0; 3) D<0, а ДКФ второй группы – на случаи наличия или отсутствия корня знаменателя. Путем формального деления числителя на знаменатель дроби ДКФ приведем ее к следующим видам: 
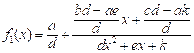(первая группа) и 
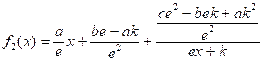(вторая группа). Если переобозначить некоторые числовые коэффициенты в выражениях для f1(x) и f2(x), то они примут, соответственно, вид 
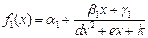и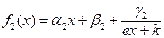 
. Для f1(x) возможны две разновидности функций: 1) β1=0; 2) β1≠0. В приведенной ниже таблице 1 соответствующие графики f1(x) построены с помощью [3] и проиллюстрированы при конкретных значениях параметров α1, β1, γ1, d, e, k.
Таблица 1
Классификация функций вида f1(x)
|
|
|
|
d |
e |
k |
Комментарий |
Общий вид графика |
|
0 |
0 |
9 |
1 |
1 |
1 |
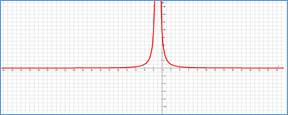
0 корней знаменателя, 1 экстремум, 2 смены выпуклости |
|
|
0 |
0 |
9 |
1 |
2 |
1 |
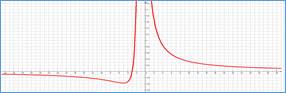
1 корень знаменателя, без экстремумов, 1 смена выпуклости |
|
|
0 |
0 |
9 |
1 |
1 |
-1 |
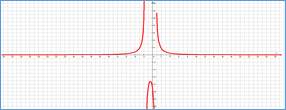
2 корня знаменателя, 1 экстремум, 3 смены выпуклости |
|
|
0 |
1 |
1 |
1 |
1 |
1 |
0 корней знаменателя, 2 экстремума, 4 смены выпуклости |
|
|
0 |
3 |
9 |
1 |
2 |
1 |
1 корень знаменателя, 1 экстремум, 3 смены выпуклости |
|
|
0 |
1 |
1 |
1 |
1 |
-1 |
2 корня знаменателя, без экстремумов, 4 смены выпуклости |
|
|
0 |
-7 |
10 |
1 |
1 |
-1 |
2 корня знаменателя, 2 экстремума, 4 смены выпуклости |
|
Для функций f2(x) соответствующая классификация представлена в таблице 2.
Таблица 2
Классификация функций f2(x)
|
|
|
|
e |
k |
Комментарий |
Общий вид графика |
|
1 |
0 |
1 |
1 |
1 |
1 корень знаменателя, 2 экстремума, 1 смена выпуклости |
|
|
1 |
0 |
-1 |
1 |
1 |
1 корень знаменателя, нет экстремумов, 1 смена выпуклости |
|
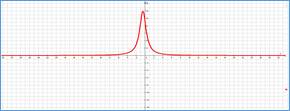
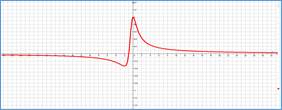
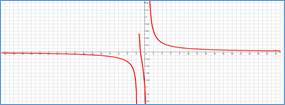
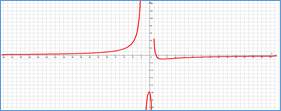
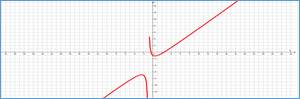
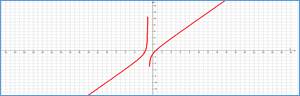
Рассмотрим далее практический пример обучающего характера и приведем методику его анализа с использованием дробно-квадратичной функции и графоанализатора. Пусть у производственного предприятия имеется возможность извлечь из некоторого бизнеса экономический потенциал в размере W денежных единиц (д.е.) путем реализации двух альтернативных сценариев: 1) при условии равномерных усилий w д.е. в единицу времени (ед. вр.) и 2) при условии, что половину потенциала оно будет функционировать с уменьшенными (увеличенными) на с д.е./ед.вр. усилиями, а вторую половину – соответственно с увеличенными (уменьшенными) на ту же величину с усилиями. Требуется ответить на вопрос, какой из вариантов приведет к скорейшему достижению экономического потенциала W. Сформулированная задача может быть решена аналитически, но допускает и оперативный ответ на вопрос с использованием пакета [3]. С этой целью достаточно построить и визуально сравнить [7] две функции: F1(w)=W/w и F2(w)=W/(w2–а2). Методика применения графоанализатора в данном случае имеет следующий алгоритм. В нотации пакета [3] cтроятся две функции: a*/(b*x+0.0001) и a/(x^2-c^2), соответствующие частным случаям рассмотренной выше ДКФ. При этом слагаемое +0.0001 используется в знаменателе первой функции, чтобы избежать деления на ноль при инициировании работы программы, и практически не влияет на точность получаемых зависимостей. Перебирая средствами пакета значения параметра с при фиксированных значениях параметров а и b, из фрагментов графиков на рисунке убеждаемся, что для всех значений переменной w и параметра с выполняется неравенство F1(w)<F2(w), что, очевидно, свидетельствует в пользу равномерных усилий предприятия для достижения своего экономического потенциала. Анализ задачи при этом занимает незначительное время (не более нескольких минут для внесения формул и миллисекунды для варьирования значениями параметров), что позволяет многократно использовать его в процессе проведения учебных занятий в образовательных учреждениях.
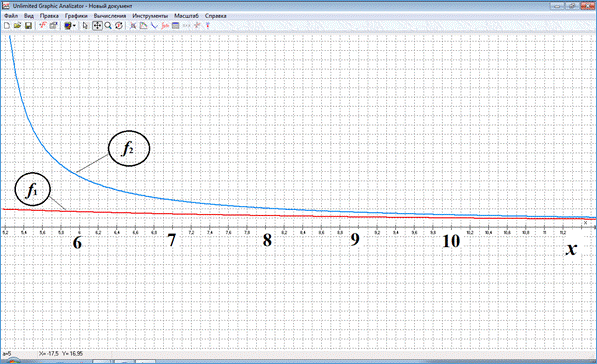
Графики временных затрат сценариев (a - любое положительное число, b=1, c=5)
Заключение
Свойства ДКФ, связанные с наличием асимптот, количеством точек разрыва промежутков монотонности и смен выпуклости, в частности, определяют и свойства решений прикладных задач с описываемыми ДКФ моделями, соответствующие примеры анализа которых с использованием графоанализатора рассмотрены в работах [7-10]. Таким образом, с учетом описанных возможностей графоанализатора [3] очевидны целесообразность и эффективность применения подобных вычислительно-аналитических комплексов для анализа различных закономерностей изучаемых в образовательных учреждениях явлений и процессов.
Библиографическая ссылка
Медведев А.В. ПРИМЕНЕНИЕ ПАРАМЕТРИЧЕСКОГО ГРАФОАНАЛИЗАТОРА ДЛЯ РЕШЕНИЯ УЧЕБНЫХ И ПРИКЛАДНЫХ ЗАДАЧ ЕСТЕСТВЕННОНАУЧНОГО И ЭКОНОМИЧЕСКОГО СОДЕРЖАНИЯ // Современные проблемы науки и образования. – 2021. – № 5. ;URL: https://science-education.ru/ru/article/view?id=31095 (дата обращения: 24.04.2024).