Переход на новые стандарты образования остается одной из главных проблем современной педагогической науки и практики. Необходима теоретическая и методическая проработка вопросов внедрения новых стандартов.
Вопрос развития универсальных учебных действий в настоящее время является актуальным. Предмет «Математика», в частности курс школьной геометрии, по своему содержанию и организации способов учебной деятельности создает возможности для развития у учащихся регулятивных и познавательных универсальных учебных действий.
Цель исследования – разработка методических рекомендаций по развитию регулятивных и познавательных универсальных учебных действий учащихся в процессе обучения геометрическому материалу в 5-м классе.
Материал и методы исследования
В федеральном государственном образовательном стандарте представлены требования к личностным, метапредметным и предметным результатам [1].
Универсальные учебные действия включаются в метапредметные результаты.
В составе универсальных учебных действий выделяют четыре блока: личностный, регулятивный, познавательный и коммуникативный [2].
Большое внимание в сфере развития регулятивных универсальных учебных действий уделяется формированию действия целеполагания, которое включает способность ставить учебные цели и задачи, планировать их реализацию, осуществлять выбор эффективных путей и средств достижения целей, контролировать и оценивать свои действия, вносить необходимые коррективы в их выполнение [3].
Большое внимание в сфере развития познавательных универсальных учебных действий уделяется практическому освоению методов познания, соответствующего им инструментария и понятийного аппарата, систематическому использованию общеучебных умений, знаково-символических средств, логических действий и операций [3].
Учитель, который создает урок в соответствии с федеральным государственным образовательным стандартом, должен соблюдать следующие правила: учениками формулируются цели урока; учитель обучает учеников осуществлять рефлексивное действие; учитель использует разные формы, методы и приемы обучения, которые повышают активность учащихся; учитель учит учеников работать по плану; и др. [4].
Выделяют следующие действия учителя по формированию регулятивных универсальных учебных действий: учитель учит учеников определять цель урока, план действия; учитель учит учеников формулировать алгоритм выполнения задания; учитель учит учеников находить рациональные способы решения; учитель учит учеников способам самопроверки, взаимопроверки; и др. [4].
Выделяют следующие действия учителя по формированию познавательных универсальных учебных действий: учитель учит учеников составлять графики, схемы, таблицы, создавать модели; учитель учит учеников решать задачу разными способами; учитель учит учеников анализировать, обобщать; и др. [4].
При развитии у учеников регулятивных и познавательных универсальных учебных действий важная роль отводится изучению материала пропедевтического курса геометрии.
Результаты исследования и их обсуждение
Рассмотрим возможности развития регулятивных и познавательных универсальных учебных действий учащихся на примере обучения геометрическому материалу в 5-м классе.
В начальной школе начинается процесс формирования универсальных учебных действий учащихся, работа в этом направлении продолжается в 5-м классе. Геометрия считается одним из сложных школьных учебных предметов. Знакомство с геометрическим материалом в 5-м классе способствует подготовке к восприятию более сложного материала систематического курса геометрии.
В 5-м классе учащиеся знакомятся с различными геометрическими величинами: длиной, площадью, объемом. Для развития регулятивных и познавательных универсальных учебных действий при обучении геометрическому материалу в 5-м классе целесообразно использовать различные виды заданий.
Рассмотрим примеры заданий, которые способствуют развитию познавательных и регулятивных универсальных учебных действий.
В качестве домашнего задания перед изучением темы «Площадь. Формула площади прямоугольника» ученикам можно предложить составить задачу с использованием старинных мер длины. В начале урока проводится проверка в парах.
Для формулировки темы урока при изучении темы «Площадь. Формула площади прямоугольника» ученики разгадывают кроссворд (рис. 1).
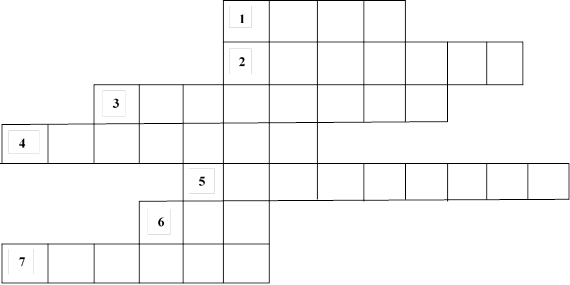
Рис. 1. Кроссворд
Вопросы
1. Расстояние между концами расставленных большого и указательного пальцев.
2. Инструмент, с помощью которого можно найти длину отрезка.
3. Единица измерения, равная 1000 м.
4. Единица измерения больших расстояний на Руси, равная 1 км 67 м.
5. Единица измерения, равная 10 мм.
6. Единица длины в Англии и США, равная 91 см.
7. Расстояние от концов пальцев до локтя согнутой руки.
После записи ответов ученики смогут сформулировать тему урока.
Для постановки цели урока целесообразно использовать прием «Задом наперед» [4].
На этапе формулировки цели урока при изучении темы «Площадь. Формула площади прямоугольника» ученики выполняют самостоятельную работу, состоящую из трех задач. Для решения одной задачи из этой самостоятельной работы необходимо знать формулу для вычисления площади прямоугольника.
Приведем пример самостоятельной работы.
Задача 1. Сторона MN треугольника MNP меньше стороны MP на 5 см, но больше стороны NP на 15 см, периметр треугольника MNP равен 50 см. Чему равна длина каждой стороны треугольника MNP?
Задача 2. Периметр прямоугольника равен 80 см, а длина прямоугольника в 3 раза больше его ширины. Чему равна длина каждой стороны прямоугольника?
Задача 3. Ширина прямоугольника в 4 раза меньше длины, а длина прямоугольника равна 40 см. Найдите площадь прямоугольника.
При решении третьей задачи у учеников возникнут трудности. Затем ученики вместе с учителем формулируют цели изучения темы.
На этапе закрепления нового материала по теме «Площадь. Формула площади прямоугольника» ученикам можно предложить выполнить следующие задания.
Задание 1. Составьте задачу с величинами «длина», «ширина», «площадь» по выражению: 200:4.
Ученики работают самостоятельно, а затем проводится проверка в парах.
Задание 2. Заполните таблицу (табл.).
Таблица
Задание 2
|
a |
10 см |
8 м |
|
|
b |
5 см |
|
3 дм |
|
s |
|
40 м2 |
30 дм2 |
После заполнения таблицы осуществляется самопроверка с помощью слайда.
Задание 3. Нарисуйте фигуру той же площади, что и фигура на рисунке (рис. 2), но другой формы. Длина стороны клетки равна 1 см.
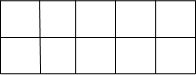
Рис. 2. Задание 3
Ученики работают самостоятельно, а затем проводится проверка в парах.
Задание 4. Длина прямоугольника 12 см, а ширина прямоугольника 4 см. Верно ли найдена площадь?
1) 4+12=16 (см)
2) 4•12=48 (см2)
3) 4•12=48 (см)
4) 4•12=46 (см2)
Самопроверка осуществляется с помощью слайда.
Задание 5. Выполните задание с использованием программы «Живая геометрия».
1. Начертите произвольный прямоугольник с использованием программы «Живая геометрия».
2. Измерьте длину прямоугольника с использованием программы «Живая геометрия».
3. Измерьте ширину прямоугольника с использованием программы «Живая геометрия».
4. Вычислите площадь прямоугольника с использованием формулы.
5. Вычислите площадь прямоугольника с использованием программы «Живая геометрия».
6. Сравните полученные значения.
На рисунке 3 представлен возможный вариант выполнения задания с использованием программы «Живая геометрия».
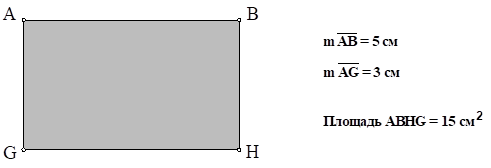
Рис. 3. Результат выполнения задания 5 с использованием программы «Живая геометрия»
Сюжетная задача является одним из эффективных учебных заданий, направленных на развитие регулятивных универсальных действий.
Рассмотрим пример.
Задача. Длина прямоугольного участка 50 м, а его ширина на 10 м меньше длины. Найдите площадь участка.
Ученики могут решить данную задачу двумя способами.
Рассмотрим первый способ.
Составление плана решения:
1. Найти ширину прямоугольного участка.
2. Найти площадь участка.
Исполнение плана решения:
1) 50 – 10=40 (м) – ширина прямоугольного участка;
2) 50•40=2000 (м2) – площадь участка.
Ответ. Площадь участка 2000 м2.
Второй способ решения данной задачи с помощью графовой модели [5].
Графовая модель задачи представлена на рисунке 4.
s, м2 – площадь участка;
a, м – длина участка;
b, м – ширина участка;
d, м – результат разностного сравнения.
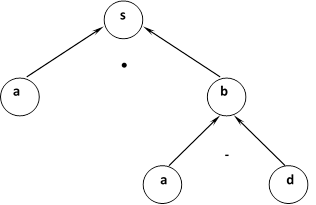
Рис. 4. Графовая модель
По графовой модели ученики получают знаковую решающую модель задачи:
1) 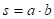
2) 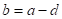
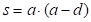
В качестве домашнего задания после изучения темы «Площадь. Формула площади прямоугольника» ученикам можно предложить подготовить доклад на тему «Измерение площади в древности».
На этапе закрепления знаний после изучения темы «Единицы измерения площадей» развитию познавательных универсальных учебных действий будет способствовать выполнение следующих заданий.
Задание 1. Исключите лишнее: мм2, см2, м2, км2, дм, га, а.
Задание 2. Восстановите цепочку вычислений (рис. 5).

Рис. 5. Задание 2
Задание 3. В клеточку вставьте знак =, < или >.
300 мм2  3 см2
3 см2
50 см2  5 дм2
5 дм2
7000 дм2  7 м2
7 м2
200 м2  2а
2а
Самопроверка осуществляется с помощью слайда.
В статье рассмотрены примеры заданий, которые способствуют развитию регулятивных и познавательных универсальных учебных действий учащихся, а также методика их использования при обучении геометрическому материалу в 5-м классе. Эти примеры позволяют сделать следующие выводы.
В процессе обучения геометрическому материалу в 5-м классе с целью развития регулятивных и познавательных универсальных учебных действий учащихся целесообразно использовать следующие задания и приемы:
– задания, с помощью которых ученики смогут сформулировать тему и цели урока;
– задания на нахождение разных способов решения задачи;
– задания на составление задач;
– задания «Поиск лишнего»;
– прием «Заполни пропуски»;
– прием «Лови ошибку»;
– построение моделей;
– применение способов самоконтроля и взаимопроверки;
– использование средств информационных технологий и др.
Систематическое использование в процессе обучения геометрическому материалу в 5-м классе различных видов заданий, которые повышают активность учеников, способствует развитию регулятивных и познавательных универсальных учебных действий школьников.
Заключение
Формирование способности учащихся реализовывать регулятивные и познавательные универсальные учебные действия позволяет ученикам самостоятельно ставить цели, находить пути и средства их достижения, контролировать и оценивать свои действия, способствует повышению эффективности образовательного процесса.
Таким образом, в процессе обучения геометрическому материалу в 5-м классе реализуется задача развития регулятивных и познавательных универсальных учебных действий.
Библиографическая ссылка
Бакланова Н.А. РАЗВИТИЕ РЕГУЛЯТИВНЫХ И ПОЗНАВАТЕЛЬНЫХ УНИВЕРСАЛЬНЫХ УЧЕБНЫХ ДЕЙСТВИЙ УЧАЩИХСЯ В ПРОЦЕССЕ ОБУЧЕНИЯ ГЕОМЕТРИЧЕСКОМУ МАТЕРИАЛУ В 5-М КЛАССЕ // Современные проблемы науки и образования. 2021. № 3. ;URL: https://science-education.ru/ru/article/view?id=30910 (дата обращения: 05.02.2026).
DOI: https://doi.org/10.17513/spno.30910



