Традиционно в школьном курсе математики одной из основных содержательно-методических линий является изучение уравнений и неравенств. Очень многие учащиеся испытывают трудности при решении неравенств, относящихся к повышенному и высокому уровню сложности. Несмотря на это, к решению неравенства, требующего развернутого ответа, на едином государственном экзамене по математике профильного уровня (задание 15) приступает достаточное количество экзаменуемых. Однако далеко не все они получают максимальный балл за выполнение этого задания. Решению задач подобного рода на ЕГЭ посвящено достаточно много методических исследований (например, [1-3]). В данном исследовании затрагиваются некоторые аспекты применения метода интервалов к решению комбинированных неравенств.
Материал и методы исследования
Для выявления типичных ошибок и составления рекомендаций по их предупреждению был проведен детальный анализ решений заданий № 15 второй части ЕГЭ по математике профильного уровня.
Результаты исследования и их обсуждение
Комбинированные неравенства очень разнообразны по своему виду и предполагают применение различных методов в решении. В ряде случаев возможно разложение на множители и рассмотрение систем условий, равносильных исходному неравенству, имеет место применение метода интервалов или метода рационализации, кроме того, возможны и нестандартные приемы. Конечно, при обучении школьников работе с неравенствами необходимо стремиться к тому, чтобы учащиеся могли в каждом конкретном случае выбирать метод, который будет минимален по временным затратам в рамках экзамена, не будет содержать громоздких вычислений и не приведет к ошибкам. Эти вопросы требуют высокого уровня математической культуры. В силу ограниченности учебного времени сформировать такие умения удается далеко не всегда. Очень часто школьники воспринимают алгоритмы решения каждого конкретного типа неравенства (рационального, показательного, логарифмического и т.д.), но испытывают трудности при работе с комбинациями в одном неравенстве. Метод интервалов является одним из тех методов, который можно применять к неравенствам любого типа. Алгоритм, лежащий в его основе, делает этот метод привлекательным для учащихся, дает возможность применения этого метода даже если он не совсем осознан ими. Многие дети просто запоминают порядок действий, не анализируя каждой конкретной ситуации. А иногда и не выполняют всех шагов решения, считая, что можно действовать по аналогии с рациональными неравенствами. Однако, для того чтобы метод интервалов стал универсальным, необходимо четко представлять его математическую основу, связь его с функциональной линией.
Напомним, что метод интервалов основан на исследовании промежутков знакопостоянства функции. Пусть нам дано неравенство вида 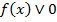 , где Ú - это один из знаков неравенства (>, <, ³, £). Множество решений данного неравенства совпадает со множеством значений аргумента функции
, где Ú - это один из знаков неравенства (>, <, ³, £). Множество решений данного неравенства совпадает со множеством значений аргумента функции 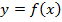 , для которых значения функции имеют тот же, что и у неравенства, знак. Поэтому необходимо исследовать промежутки знакопостоянства этой функции. В основе определения знаков непрерывной на некотором интервале функции лежит теорема Больцано-Коши [4, с. 168] (которую школьникам, конечно, доказывать не представляется возможным), однако она дает нам лишь необходимое, но не достаточное условие для смены знака функции. Т.е. если непрерывная функция принимает в некоторой точке значение, равное нулю, то в этой точке возможна смена знака. Аналогичное утверждение можно сформулировать и для функций, терпящих разрыв в некоторой области: при переходе через точку (интервал) разрыва функция может (но не обязана) поменять свой знак. Из вышеприведенных очевидных умозаключений и вытекает известный большинству учащихся алгоритм метода интервалов:
, для которых значения функции имеют тот же, что и у неравенства, знак. Поэтому необходимо исследовать промежутки знакопостоянства этой функции. В основе определения знаков непрерывной на некотором интервале функции лежит теорема Больцано-Коши [4, с. 168] (которую школьникам, конечно, доказывать не представляется возможным), однако она дает нам лишь необходимое, но не достаточное условие для смены знака функции. Т.е. если непрерывная функция принимает в некоторой точке значение, равное нулю, то в этой точке возможна смена знака. Аналогичное утверждение можно сформулировать и для функций, терпящих разрыв в некоторой области: при переходе через точку (интервал) разрыва функция может (но не обязана) поменять свой знак. Из вышеприведенных очевидных умозаключений и вытекает известный большинству учащихся алгоритм метода интервалов:
1) найти область определения функции;
2) найти нули функции;
3) определить знаки на каждом из промежутков, на которые нули функции разбили область определения.
Особых трудностей с запоминанием и пониманием этого алгоритма не возникнет, если уже в 9 классе [5, с. 65] при изучении рациональных неравенств (начиная с квадратных) учащимся объяснять связь между функциональной линией и решением неравенства. Проблемы применения метода интервалов к решению комбинированных неравенств возникают по большей части тогда, когда дети привыкают при работе с дробно-рациональными неравенствами действовать бездумно по шаблону: найдите нули числителя, нули знаменателя и т.д. Сразу отметим, что из этого же следуют и ошибки с включением или исключением концов интервала в решение (закрашенные и выколотые точки). Поэтому, начиная работать с методом интервалов, прежде всего обращаем внимание на отыскание области определения: функция может быть определена не на всей числовой прямой. Поэтому в рациональных неравенствах нули знаменателя это не что иное, как область определения функции; точки, не входящие в область определения, не могут войти в решение исходного неравенства. В более сложных неравенствах, на тех промежутках, где функция не существует, просто бессмысленно говорить что-либо о ее знаке. Следующее, на что необходимо обращать внимание, это определение знаков функции на конкретных промежутках. Если говорить о рациональных неравенствах, то там очень многие учащиеся успешно пользуются правилом, позволяющим определять знаки «автоматически», опираясь на четность или нечетность степени линейных множителей, входящих в неравенство. На наш взгляд, для школьников очень опасно делать аналогичные выводы при работе с комбинированными неравенствами, особенно когда соответствующие функции имеют разрывы.
На экзамене по математике профильного уровня в 2020 году предлагалось комбинированное неравенство следующего вида:
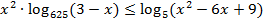 . (1)
. (1)
При решении этого задания многие выпускники прибегали к использованию метода интервалов. Большинство из них правильно выполняли равносильные преобразования и приходили к неравенству 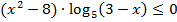 .
.
Следует отметить, что уже из оформления работы можно сделать вывод о том, четко ли учащийся представляет себе математический аппарат, лежащий в основе применяемого им метода. Ненаписание «лишней» строки «рассмотрим функцию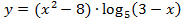 » и использование термина «ОДЗ» вместо «область определения функции» не являются ошибками, но заставляют задуматься об уровне математической культуры. Одной из самых распространенных ошибок в решении, не влияющей на ответ, являлось то, что дети, найдя нули функции, как решения соответствующего уравнения, наносили их на числовую прямую без учета области определения функции, расставляли знаки на всей числовой прямой, затем отбирая значения с учетом области допустимых значений логарифма (рис. 1).
» и использование термина «ОДЗ» вместо «область определения функции» не являются ошибками, но заставляют задуматься об уровне математической культуры. Одной из самых распространенных ошибок в решении, не влияющей на ответ, являлось то, что дети, найдя нули функции, как решения соответствующего уравнения, наносили их на числовую прямую без учета области определения функции, расставляли знаки на всей числовой прямой, затем отбирая значения с учетом области допустимых значений логарифма (рис. 1).
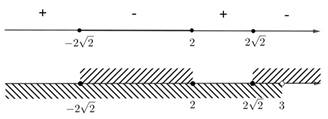
Рис. 1. Ошибка в применении метода интервалов
Это позволяет сделать выводы о том, что, во-первых, выпускник не понимает математический смысл метода интервалов, и, во-вторых, либо ему «повезло» при определении знаков на каждом промежутке, либо он их просто расставил «через один».
Чтобы избежать ошибок подобного рода при решении комбинированных неравенств, необходимо предлагать учащимся задания, содержащие разрывные функции. Тренировочные задания должны содержать функции, имеющие точечные или интервальные разрывы, с сохранением или сменой знака. Работа с такими неравенствами позволит увидеть особенности реализации метода интервалов.
Пример 1. Первое неравенство содержит функцию, не определенную на некотором интервале числовой прямой.
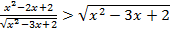 .
.
Равносильным образом преобразуем неравенство: перенесем правую часть влево и приведем к общему знаменателю:
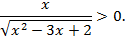
Числитель обращается в 0 при x = 0, знаменатель равен 0 при х = 2 или x = 1. Область определения функции, находящейся в левой части неравенства, является решением неравенства 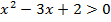 и представляет собой объединение двух интервалов:
и представляет собой объединение двух интервалов: 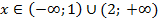 . Функция
. Функция 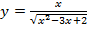 имеет два бесконечных разрыва в точках 1 и 2. Бесконечные односторонние пределы в этих точках одного знака. Поведение функции легко проследить по её графику, приведённому на рисунке 2. Определяя знаки дроби на интервалах, будем иметь:
имеет два бесконечных разрыва в точках 1 и 2. Бесконечные односторонние пределы в этих точках одного знака. Поведение функции легко проследить по её графику, приведённому на рисунке 2. Определяя знаки дроби на интервалах, будем иметь:
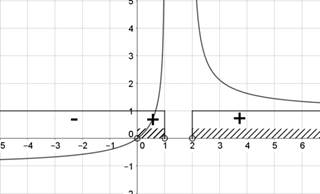
Рис. 2. График функции 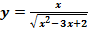
Пример 2. Следующая серия комбинированных неравенств содержит композицию логарифмической и дробно-рациональной функции. Эта сложная функция, как и в предыдущем примере, определена на объединении двух бесконечных интервалов числовой прямой, имеет два бесконечных разрыва, но в отличие от предыдущего случая бесконечные односторонние пределы в точках разрыва имеют разные знаки:
а) 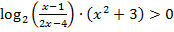 .
.
Допустимыми значениями переменной в этом неравенстве является объединение двух интервалов: 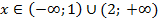 . По графику функции
. По графику функции 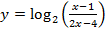 на рисунке 3 проследим её поведение.
на рисунке 3 проследим её поведение.
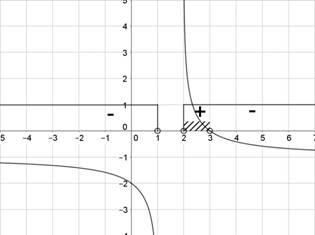
Рис. 3. График функции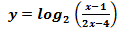
Вернемся к решению неравенства. Второй множитель произведения в левой части неравенства не влияет на знак произведения. К сожалению, не все ученики смогут «решиться» на деление обеих частей неравенства на выражение, содержащее переменную. Это «запретное» действие (ведь учитель на уроке много раз подчеркивал, что делить на переменную нельзя) могло бы свести исходное неравенство к простейшему логарифмическому неравенству 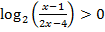 , решение которого не составило бы труда.
, решение которого не составило бы труда.
Чаще срабатывает «алгоритмическое» мышление, поэтому можно ожидать, что ученик найдет нули функции 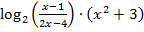 , точку x = 3, отметит на числовой прямой эту точку и область определения функции, расставит знаки функции на интервалах. При этом ученик может ошибочно рассудить, что знак поменяется только при переходе через ноль функции. Ошибка избегается путем определения знака на каждом интервале. Но ученик «настроен» на чередование знака, тем более что кратных корней он здесь не видит, а определение знака числовых выражений, содержащих логарифмы, зачастую вызывает трудности. Такая логика приведет к ошибке. И только обращение к графику функции поможет увидеть распределение знаков (рис. 3);
, точку x = 3, отметит на числовой прямой эту точку и область определения функции, расставит знаки функции на интервалах. При этом ученик может ошибочно рассудить, что знак поменяется только при переходе через ноль функции. Ошибка избегается путем определения знака на каждом интервале. Но ученик «настроен» на чередование знака, тем более что кратных корней он здесь не видит, а определение знака числовых выражений, содержащих логарифмы, зачастую вызывает трудности. Такая логика приведет к ошибке. И только обращение к графику функции поможет увидеть распределение знаков (рис. 3);
б) во втором неравенстве можно предложить произведение той же логарифмической функции 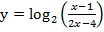 со знакопеременным множителем. Например, такое неравенство
со знакопеременным множителем. Например, такое неравенство
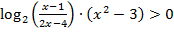 .
.
Второй множитель еще более затруднит определение знаков на интервалах методом подстановки значений переменной, уж очень интервалы «малы». Какие варианты выхода из затруднительной ситуации может выбрать ученик? Обратиться к графику функции 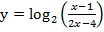 , перейти от данного неравенства к совокупности двух систем, чередуя знаки множителей, все-таки оценивать знак логарифма на каждом интервале, главное, чтобы он видел это затруднение, а не «автоматически» расставлял знаки, оценивая порой и на участках, где функции не существуют. Окончательная расстановка знаков на числовой прямой для этого неравенства имеет следующий вид (рис. 4).
, перейти от данного неравенства к совокупности двух систем, чередуя знаки множителей, все-таки оценивать знак логарифма на каждом интервале, главное, чтобы он видел это затруднение, а не «автоматически» расставлял знаки, оценивая порой и на участках, где функции не существуют. Окончательная расстановка знаков на числовой прямой для этого неравенства имеет следующий вид (рис. 4).
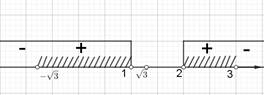
Рис. 4. Расстановка знаков для неравенства 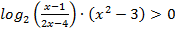
Пример 3. Следующая серия неравенств содержит функцию 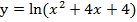 , которая определена на всей числовой прямой за исключением одной точки -2. В ней функция имеет бесконечный разрыв, бесконечные односторонние пределы в этой точке имеют одинаковый знак.
, которая определена на всей числовой прямой за исключением одной точки -2. В ней функция имеет бесконечный разрыв, бесконечные односторонние пределы в этой точке имеют одинаковый знак.
Рассмотрим неравенство 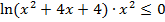 . Левая часть неравенства обращается в 0 в точках -3, -1, 0, точка -2 не принадлежит области определения неравенства. Отметим все точки на числовой прямой, расставим знаки левой части неравенства на образовавшихся интервалах, используя график функции (рис. 5а).
. Левая часть неравенства обращается в 0 в точках -3, -1, 0, точка -2 не принадлежит области определения неравенства. Отметим все точки на числовой прямой, расставим знаки левой части неравенства на образовавшихся интервалах, используя график функции (рис. 5а).
С этой же функцией можно подобрать второй множитель так, чтобы при переходе через точку -2 знак неравенства менялся. Например, неравенство 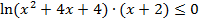 . Расстановка знаков на числовой прямой для этого неравенства представлена на рисунке 5б.
. Расстановка знаков на числовой прямой для этого неравенства представлена на рисунке 5б.
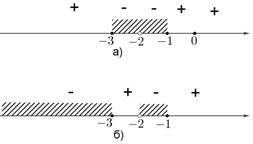
Рис. 5. Расстановка знаков для неравенств в примере 3
В каждом из рассмотренных примеров функции имели бесконечные разрывы. Школьникам довольно сложно оценить характер разрыва функции, сложным вопросом будет и определение знаков односторонних пределов, построение графиков функций. Для облегчения решения этих проблем можно воспользоваться графическими редакторами, которые строят графики функций по их аналитическим представлениям. В представленной работе графики были построены в программе Geogebra. Можно предложить ученикам самостоятельно построить графики функций. С целью углубления знаний школьников о пределах функций можно дать задание: восстановить вертикальные и горизонтальные асимптоты по построенным графикам. Такая работа очень полезна для формирования умения самостоятельно строить графики функций. Можно отметить, что, даже научившись проводить полное исследование функции, ученики затрудняются в построении графика по этому исследованию. Такая промежуточная работа с готовыми графиками даст им необходимый опыт, разовьет интуицию.
В связи с этим полезно будет познакомить школьников и с функциями, имеющими конечные разрывы, например с функцией 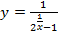 . Функция имеет конечный разрыв в нуле, односторонние пределы в этой точке разные по знаку.
. Функция имеет конечный разрыв в нуле, односторонние пределы в этой точке разные по знаку.
Заключение
Для успешного применения метода интервалов при решении комбинированных неравенств необходимо сформировать четкое понимание учащимися взаимосвязи этого метода с функциональной линией в школьном курсе математики. Необходимо расширять представления школьников о функциях, плавно переходя от элементарных функциональных зависимостей к более сложным, требующим достаточно глубоких исследований. В этом случае метод интервалов не будет восприниматься учащимися формально, на уровне алгоритма, что позволит избежать ошибок.
Библиографическая ссылка
Монахова О.А., Сорокина М.В. ОШИБКИ ПРИ РЕШЕНИИ КОМБИНИРОВАННЫХ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ И ПУТИ ИХ ПРЕДУПРЕЖДЕНИЯ // Современные проблемы науки и образования. 2021. № 2. ;URL: https://science-education.ru/ru/article/view?id=30667 (дата обращения: 04.03.2026).
DOI: https://doi.org/10.17513/spno.30667



