Не мыслям надо учить, а мыслить
И. Кант
Проблема формирования математической грамотности – как проблема качества математического образования, стимулировала инициативу правительства к разработке «Концепции развития математического образования в РФ». Она сегодня актуальна как никогда, так как обращена на радикальное совершенствование качества российского образования. В «Концепции» говорится, что математика занимает особое место в науке, культуре и обществе, являясь узловой частью научно-технического прогресса. Освоение математики – развитие познавательных способностей личности к логическому мышлению и грамотности, играет системообразующую роль в образовании российских школьников. Без преувеличения можно сказать, что высокое качество математической грамотности в стране является основой её экономической мощи и национальной безопасности. Итогом реализации математической грамотности человека является её прикладная направленность – понимание смысла науки, как универсального языка описания и познания окружающего мира [1].
Особого внимания заслуживает ситуация, требующая использования математических знаний для проверки способностей учащихся в размышлении и применении интуиции. Для этого важно иметь весомый запас математических знаний/умений, которые не сводятся к математическим фактам, терминам, стандартным методам решения и умению выполнять вычислительные действия.
Центральной и основной задачей учителя сегодня становится овладение технологией формирования математической грамотности с использованием методов/форм и средств внеурочного обучения в соответствии с задаваемыми целями и приоритетами. Современного педагога отличает новаторство во всем, и его труд сегодня должен приобретать опережающий, проектный характер.
Цель статьи – описать опыт организации математических турниров и поделиться его влиянием на формирование математической грамотности школьников. А также привить интерес к изучению предмета математика и воспитанию коллективизма, чувства долга и ответственности каждого за всех.
В соответствии с целью решаются следующие задачи мероприятия:
1. Определение участников (команд) математического турнира из разных школ города Лесосибирска.
2. Разработка заданий для 3 туров.
3. Определение критериев оценивания и прохождения в следующий тур.
4. Правила дистанционной реализации мероприятия.
5. Подведение итогов, анализ результатов и определение победителей.
Материал и методы исследования. В контексте международного тестирования в 1991 г. появилось словосочетание «математическая грамотность». В исследовании PISA «математическая грамотность - способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину» [2].
Функциональная грамотность состоит из нескольких аспектов: математической, языковой, читательской, информационной грамотности. Работа педагога всегда направлена на формирование всех вышеперечисленных аспектов.
Математическая стоит на первом месте и решает следующие задачи [3]:
- распознавание проблем, которые можно решать средствами математики;
- формулировка проблемы в виде модели на языке математики;
- решение задачи средствами математических фактов и методов;
- анализ использованных методов решения;
- интерпретация и формулировка полученных результатов;
- запись результата решения.
Мы учли три составляющие математической грамотности, описанные в программе PISA:
- умение находить/отбирать нужную информацию;
- выполнять арифметические действия и применять их на практике;
- интерпретировать/сопоставлять, оценивать и анализировать данные.
А задания, по которым в мероприятии оценивается математическая грамотность, основываются на жизненных, исторических или реальных ситуациях, интересных ребятам в силу возраста. Сами задачи включают жизненно-проблемный материал, представленный через текст, графику, таблицы и связанные с ними вопросы.
Для проверки уровня математической грамотности необходимо разработать диагностику, которая позволит оценить знания, понять причины трудностей и найти способы их устранения. В этом деле нам помогла серия пособий «Педагогическая диагностика» Л.Е. Журовой, Е.Э. Кочуровой, М.И. Кузнецовой, А.О. Евдокимовой.
Встал вопрос: как развить математическую грамотность? Эффективно стимулирует интерес к точной науке соревновательное движение в виде математических турниров, викторин и эстафет. Соревновательность (интеллектуальная) - фактор развития личности, укрепления и закалки характера, закрепление уверенности в своих знаниях и приобретение новых. Склонность творчески одаренного ребенка к соревновательности отмечают многие специалисты-психологи. Опыт побед и поражений, приобретаемый ребенком в ходе интеллектуальных состязаний, является беспроигрышным и рассчитан на формирование новых знаний. Кроме того, к любому состязанию, даже интеллектуальному математическому турниру, необходима серьезная подготовка. О турнире объявляется заранее, и ребята вместе с руководителями ведут творческую подготовку, пополняя багаж математической грамотности. В ходе состязания ставились цели обмена математическими знаниями, развития умения систематизировать и доказывать, сравнивать и представлять аналогии. Девизом станут слова: «Соревнуясь – учимся», а нестандартные задачи потребуют от участников описания своих действий, и оцениваться будет именно ход мысли детей.
В нашем проекте математический турнир организуется по принципу: команды состоят из всех желающих принять участие независимо от способностей и уровня математической подготовки. Социализация личности в маттурнире – еще одна важна проблема. Ее решение заключается в попытке выстроить систему соревнований, в которой возрастает роль участника от первого тура игры к последующему; от краткого письменного ответа на вопрос задачи в 1-м и 2-м турах до устной дискуссии в проекте на последнем.
В нашем вузе математические соревнования в виде математического турнира или олимпиады проводятся ежегодно с целью повышения интереса у школьников к математике, расширения их кругозора, выявления одаренных учащихся города. Турниры по математике готовятся и проводятся исключительно силами энтузиастов – преподавателей кафедры высшей математики, информатики и естествознания Лесосибирского педагогического института – филиала СФУ.
Результаты исследования и их обсуждение. В этом учебном году математический турнир был организован в дистанционной форме. В увлекательные дистанционные конкурсы вовлекают всех желающих независимо от географического положения школ и временных ограничений, ребята получают равные возможности и права. Для размещения заданий использовались Google-формы, которые позволили организовать моментальную обратную связь. Были использованы следующие формы тестовых заданий:
- «текст (строка)», являющаяся открытой формой тестовых заданий и предполагающая ввод краткого ответа в виде текста или числа;
- «сетка флажков», реализующая тестовую форму на соответствие;
- «несколько из списка», представляющая собой закрытую форму тестовых заданий с множественным выбором ответов.
Все ответы заносятся в соответствующую Google-таблицу, что позволяет ускорить процесс анализа результатов для прохождения по этапам. Также автоматически проводится анализ ответов на каждый вопрос и строится диаграмма.
Отметим, что внедрение формул в Google-формы вызывает большие сложности, что актуально для математики. Однако есть возможность сопровождать тестовые задания иллюстрациями путем внедрения графических изображений, в том числе и изображений формул. Работа ведется системно и поэтапно, ребятам предлагается справиться с заданиями по уровням:
1 уровень. Задачи на выполнение вычислений, воспроизведение фактов и методов.
2 уровень. Ситуационные задачи на выделение математической проблемы и построение модели решения средствами математики.
3 уровень. Участие в проекте, где требуется умение интегрировать материал из разных областей человеческой деятельности.
При составлении пакета заданий преподаватели опирались на правила [4]:
- подбирали задания, решение которых можно изложить вкратце;
- задания 1-го тура должны быть простыми и решаемыми большинством участников;
- задания каждого тура имеют различную текстовую тематику, но примерно одинаковый уровень сложности;
- время, отводимое на выполнение заданий, и сложность самих заданий возрастают от тура к туру.
Каждому школьнику, участвующему в турнире, предоставляется возможность:
- выбирать и выполнять задания по допустимой сложности;
- приобретать навыки коллективной деятельности в учебе;
- сравнить свое решение с правильным и быстро получать балл результатов;
- демонстрировать навыки проведения исследования по объявленной теме (проект).
Опишем задания второго тура для учащихся 8 класса.
Тема: Цветочная клумба [5]. Фирма, которая занимается ландшафтным дизайном, высаживает на кольце возле администрации города Лесосибирска цветы в форме круга. На рисунке 1 ниже изображены схемы посадки клубней тюльпанов для нескольких значений n, где n – количество кругов. Эту последовательность можно продолжить для любого числа n.
Вопрос 1. Заполните таблицу 1, подсчитав необходимое количество клубней тюльпанов для пяти кругов. Для подсчета используйте схемы, представленные на рисунке 1.
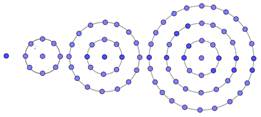
Рис. 1. Схемы посадки клубней тюльпанов
Таблица 1
Зависимость количества клубней тюльпанов от количества кругов
|
n |
Число кругов |
Количество клубней тюльпанов |
|
1 |
1 |
1 |
|
2 |
2 |
9 |
|
3 |
3 |
25 |
|
4 |
4 |
49 |
|
5 |
|
|
Вопрос 2. В рассмотренной выше последовательности (таблица 1) число кругов и количество клубней подсчитываются следующим образом: число кругов: n; количество цветов: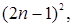 
где n – число кругов.
Сколько кругов можно получить в панно, имея 169 клубней тюльпанов? Запишите решение.
Вопрос 3. Выведите зависимость между количеством клубней и n (числом рядов) для треугольной клумбы, изображенной на рисунке 2.
Рис. 2. Схема зависимости между количеством клубней и числом рядов
В мероприятии нами используются различные формы проведения туров и методы формулировки заданий: словесные (учащиеся воспринимают и усваивают готовую информацию) - объяснительно-иллюстративный; наглядные (показ иллюстрационного материала, работа по образцу и др.) - репродуктивный; практические (творческая работа учащихся) – исследовательский.
При анализе заданий организаторы обращают внимание учащихся на то, что все задачи имеют только одно решение. Практические действия тоже очень важны – желательно предлагать участникам представлять (воображать), измерять, рисовать, сравнивать, а потом объяснять свои манипуляции. Здесь возникает возможность познакомить учеников с интересными фактами их города, истории края, новыми (нестандартными) рассуждениями. Задача организаторов позаботиться о развитии глубокого познавательного интереса и любознательности школьников. Это раскроет притягательные стороны математики и сформирует постоянный интерес и склонность к изучению предмета.
Введение федеральных государственных образовательных стандартов общего образования (ФГОС ОО) является актуальной проблемой развития современного образования [6]. Ключевым аспектом новых ФГОС определяют формирование универсальных учебных действий (УУД). А системно-деятельностный подход лежит в основе введения стандартов нового поколения. Задача учителя – развивать мышление ребенка, обучая думать. Математический турнир способствовал развитию логического мышления, математической смекалки школьников, применению знаний на практике. Турнир развивает:
- предметные (умение использовать математические знания и вычислительные навыки в нестандартной ситуации);
- метапредметные (умение доказывать свою точку зрения и проводить анализ/синтез);
- личностные (эмпатия, толерантность, соревновательность, доброжелательность) универсальные учебные действия.
Ниже приводится таблица 2 частичных результатов математического турнира.
Таблица 2
Результаты 2-го этапа, 8 класс, вопрос 3
|
Всего ответов |
Верно |
% верных |
Частично верно |
% частично верных |
Не верно |
% не верных |
|
7 |
3 |
42,86% |
0 |
0,00% |
4 |
57,14% |
Заключение. Соревнование проходило в эмоциональной атмосфере, несмотря на то что решение математических задач требует сосредоточенности и концентрации внимания. Участниками турнира стали более двухсот ребят школ г. Лесосибирска, Енисейска и Мотыгинского района. Для 3 туров были разработаны и размещены в Google-формах задания в виде: «текст (строка)» (ввод краткого ответа); «сетка флажков» (тестовая форма на соответствие) и «несколько из списка» (тестовые задания с множественным выбором ответов). К каждому этапу были разработаны критерии оценивания заданий и условия перехода участников в следующий тур, а также правила дистанционной формы проведения математического турнира (регистрации, подключения, формы представления ответов).
Содержание заданий опиралось на субъективный опыт участников, включало региональный компонент, что, несомненно, вызывало интерес и способствовало мотивации учащихся. В ходе ответов на вопросы школьники показали свои способности в определении и понимании основ математики, оперировали обоснованными математическими суждениями, демонстрируя понимание смысла науки, как универсального языка описания и познания окружающего мира – что и есть математическая грамотность.
По суммарному количеству баллов определились победители турнира. Рефлексивный опрос участников мероприятия показал, что с заданиями такого типа они столкнулись впервые. Ребята высказали желание участвовать в мероприятии такого формата и решать подобного рода математические задачи. Авторами были составлены методические рекомендации по решению заданий турнира, которыми могут воспользоваться как учащиеся, так и учителя для повышения уровня математического образования.
Статья подготовлена при поддержке краевого государственного автономного учреждения «Красноярский краевой фонд поддержки научной и научно-технической деятельности» в рамках конкурса по организации проведения мероприятий по профессиональной ориентации молодежи.
Библиографическая ссылка
Киргизова Е.В., Фирер А.В., Елисова А.П., Ахтамова С.С. МАТЕМАТИЧЕСКИЙ ТУРНИР КАК СРЕДСТВО ПОВЫШЕНИЯ УРОВНЯ МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ В ПРИЕНИСЕЙСКОМ РЕГИОНЕ // Современные проблемы науки и образования. – 2020. – № 6. ;URL: https://science-education.ru/ru/article/view?id=30423 (дата обращения: 25.04.2024).