Одним из важнейших аспектов проведения мастэктомии является создание благоприятных условий для заживления послеоперационной раны с минимально возможными нарушениями эстетической картины [1-3]. Рак молочной железы на сегодняшний момент является одним из самых распространенных видов онкологической патологии, при этом многие хирурги рассматривают вовлечение в злокачественный процесс кожи как неоперабельное локорегиональное распространение карциномы [4-6]. В некоторых случаях прорастание опухолью кожи приводит к возникновению ран, язв с их вторичным нагноением, что является абсолютным противопоказанием для проведения полихимиотерапии [7-9]. По последним данным, количество таких пациенток достигает 5-10% [10-12]. В статье обоснована необходимость проведения оперативного этапа лечения в качестве up-front терапии, а также представлен оптимальный способ закрытия дефекта кожи после проведения мастэктомии и выполнено виртуальное моделирование с целью расчета его оптимальных характеристик.
Цель исследования - выполнить топографо-анатомическое, и техническое обоснование методики послабляющих разрезов при замещении значительных дефектов кожи передней грудной стенки после радикальной мастэктомии по поводу распадающегося рака молочной железы.
Задачи:
1. Оценить результаты лечения 81 пациентки, прооперированной по поводу распадающегося рака молочной железы.
2. Произвести топографо-анатомический и математический анализ особенностей дефекта кожных покровов передней грудной стенки после радикальной мастэктомии и предложить, на основании выполненного анализа, оптимальную модель кожной пластики.
3. Выполнить виртуальное математическое моделирование предложенного способа и его сравнение с методикой, использованной в приведенных клинических примерах.
Материалы и методы исследования
В работу были включены данные о 81 пациентке, проходившей лечение в онкологическом отделении Клинической больницы им. Петра Великого и СПб ГБУЗ «Городской клинический онкологический диспансер» с 2003 по 2011 г. Возраст больных варьировал от 33 до 91 года, при этом медиана составила 59 (95% CI 54-64) лет, а среднее значение возраста - 60 (95% CI 57-63) лет. В возрасте до 50 лет были 20 (24,7%) больных, 50-59 - 22 (27,2%), 60-69 - 16 (19,8%) и 70 лет и старше - 23 (28,4%) пациентки.
Все больные имели распадающуюся опухоль с местным распространением и изъязвлением кожи (Т4), при этом стадия IIIb диагностирована у большей части женщин (49 или 60,5%), стадия IIIc выявлена у 10 (12,3%) больных и стадия IV - у 22 (27,2%) пациенток.
В основном больным проводилась модифицированная радикальная мастэктомия - 66 (81,5%), простая МЭ выполнена у 4 (4,9%) пациенток, санитарная ампутация - у 11 (13,6%) женщин. Клинический пример представлен проведением мастэктомии с последующим закрытием послеоперационного дефекта с использованием техники послабляющих разрезов.
Математическое моделирование методики послабляющих разрезов
С целью математического моделирования, всестороннего изучения и анализа предложенной методики ориентации послабляющих разрезов применялось программное обеспечение Abaqus CAE и программный комплекс Solidworks 2016. В программном комплексе SolidWorks 2016 была решена задача поиска фокусов гипербол и, по предложенному методу, построены модели зоны интереса с различными геометрическими конфигурациями послабляющих разрезов. Полученные модели импортировалась в среду математического моделирования Abaqus CAE для исследования напряжений в областях послабляющих разрезов. Поиск критических значений напряжения основан на теории Мизез-Хенки, которая утверждает, что пластичный материал начинает повреждаться в местах, где напряжение по Мизесу становится равным предельному значению. Граничные условия (нагрузки и фиксация), свойства материала были одинаковыми для всех конфигураций. Для стягивания краев модели установлена постоянная концентрированная сила 800 Па.
Результаты исследования и их обсуждение
Срок наблюдения за больными составлял от 11 до 142 месяцев (среднее значение - 46 месяцев, медиана - 40 месяцев). В неоадъювантном режиме 39 (48,1%) пациенткам проводилась химиотерапия, 12 (14,8%) - гормонотерапия, 5 (6,2%) - лучевая терапия. Практически все больные (80 или 98,8%) получили адъювантную гормонотерапию, 28 (34,6%) - адъювантную химиотерапию. Общая 3-летняя выживаемость пациенток составила 68,4 ± 5,3%. Событий (рецидивы, прогрессия) было 9 (11%). Они возникали в сроки от 8 до 106 месяцев (среднее значение - 28,5 месяцев, медиана - 17 месяцев). Бессобытийная выживаемость составила 62,6 + 5,5%.
Хирургическое лечение. При возможности проведения радикальной операции ОВ составляла 72,1 ± 5,6%, при невозможности она снижалась до 45,5 ± 15% (Chi-square = 3,6388, df = 1, log-rank test = 0,0493).
Устранение значительного дефекта кожных покровов с применением методики послабляющих разрезов
Описание данного метода далее рассмотрено на примере клинического случая. Больная М., 44 года, поступила в отделение с диагнозом «рак левой молочной железы» (рис. 1). При клинико-инструментальном обследовании диагностирована IV стадия заболевания с метастатическим поражением легких, сT4N1M1.
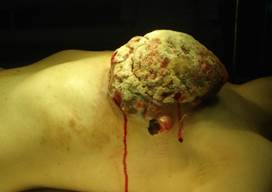
Рис. 1. Больная М., 44 лет. Диагноз «Рак левой молочной железы, IV ст., сT4N1M1»
Через 122 дня от начала системного лечения была выполнена операция в объеме санитарной ампутации левой молочной железы, которая не являлась радикальной и включала в себя только удаление органа с опухолью; при этом регионарные лимфатические узлы, а также большая и малая грудные мышцы были оставлены (рис. 4).
По причине наличия обширного послеоперационного дефекта были выполнены послабляющие разрезы – насечки на коже по сторонам раны параллельно длинной её оси (рис. 3). За счет нанесения послабляющих разрезов удалось достичь существенного снижения натяжения кожи и свести края раны.
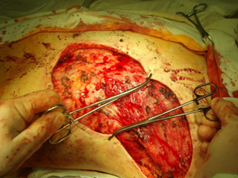
Рис. 2. Этап оперативного вмешательства (попытка стянуть края раны)
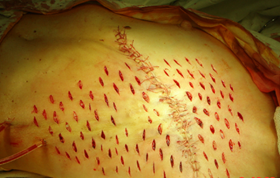
Рис. 3. Послабляющие разрезы
Несмотря на широкое распространение методики, в настоящее время не существует теоретически обоснованного метода определения оптимальной локализации послабляющих разрезов. Нами было выполнено математическое моделирование и создание оптимальной физической модели, а также сравнение последней, с применением виртуальных физических моделей, со способом нанесения послабляющих разрезов, ориентированных по большому диаметру раны.
Как видно на рисунке 4, дефект кожных покровов после радикальной мастэктомии имеет форму эллипса.
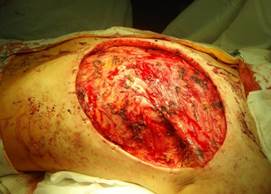
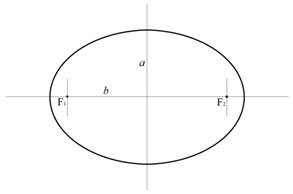
Рис. 4. Слева – вид операционной раны после радикальной мастэктомии, справа – эллипс с параметрами a и b, соответствующими длине и ширине раны; точками F1 и F2 отмечены фокусы построенного эллипса
Учитывая тот факт, что линии Лангера вокруг молочной железы располагаются в виде концентрических конфокальных эллипсов, оптимальный вектор тяги каждой точки периметра раны должен соответствовать нормали этой точки эллипса, а траектория смещения каждой точки к прямой b при стягивании раны будет соответствовать конфокальной гиперболе, проходящей через соответствующую точку (рис. 5).
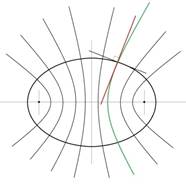
Рис. 5. Эллипс с конфокальными гиперболами: красным отмечена нормаль к конкретной точке периметра раны, зеленым – конфокальная гипербола, проходящая через эту точку
В то же время оптимальная ориентация каждого конкретного разреза будет задаваться периметром конфокального эллипса, расположенного за пределами зоны кожного дефекта, а центры предполагаемых разрезов – местами пересечений серии заданных конфокальных гипербол и эллипсов (рис. 6).
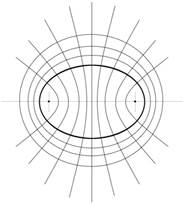
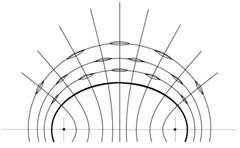
Рис. 6. Эллипс с конфокальными гиперболами и эллипсами (справа – оптимальная ориентация «послабляющих» разрезов вокруг дефекта кожных покровов эллиптической формы
Согласно нашей гипотезе, критические значения напряжений в областях разрезов зависят от геометрической конфигурации этих разрезов. С целью всестороннего изучения и анализа применяемой методики был выполнен конечно-элементный анализ области интереса для исследования нагрузок в тканях при различных геометрических конфигурациях послабляющих разрезов. В программном комплексе SolidWorks 2016 была решена задача поиска фокусов гипербол и, по предложенному методу, построены модели зоны интереса с различными геометрическими конфигурациями послабляющих разрезов и с допущением: исследуемый участок упрощен до параллелепипеда (рис. 7).
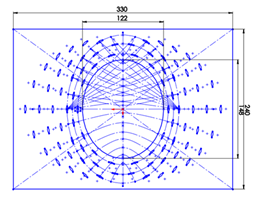
Рис. 7. Чертеж предложенной модели в программном комплексе SolidWorks 2016
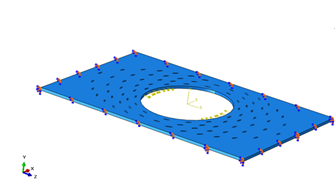
Рис. 8. Граничные условия для предложенной модели
Полученная модель была импортирована в среду математического моделирования Abaqus CAE для исследования напряжений в областях послабляющих разрезов. Поиск критических значений напряжения был основан на теории Мизез-Хенки, которая утверждает, что пластичный эластичный материал начинает повреждаться в местах, где напряжение по Мизесу становится равным предельному значению. Исходя из этого, нами была сформирована задача – подобрать оптимальную геометрическую конфигурацию послабляющих разрезов таким образом, чтобы значение критических значений напряжения было как можно большим и при этом сохранялась возможность эффективно стягивать края раны. Граничные условия (нагрузки и фиксация), свойства материала были одинаковыми для всех конфигураций (рис. 8). Для стягивания краев модели установлена постоянная концентрированная сила 800 Па.
Были приняты следующие механические свойства модели: коэффициент Пуассона – 0,2, модуль Юнга – 2 МПа; было допущено, что материал изотропен [5]. Сгенерированная сетка конечных элементов неструктурирована и содержит 41430 гексаэдров.
Были созданы 3 подобные модели: модель a, имитирующая предлагаемую геометрическую конфигурацию с расположением центров разрезов в точках пересечения конфокальных эллипсов и гипербол, модель b, послабляющие разрезы в которой располагаются без определенного порядка (на усмотрение хирурга), и модель c, аналогичная предыдущей, но с большим количеством разрезов. Общее количество послабляющих разрезов в модели a составило 84, в модели b – 60, а в модели с – 90. Для всех трёх моделей было смоделировано 15-секундное стягивание краев с шагом 0,02 секунды. Результаты, полученные в процессе эпюры, можно интерпретировать как подтверждение нашей гипотезы: критическое значение напряжения в модели a с предложенной нами геометрической конфигурацией выше (374,4 Па), чем в модели b с послабляющими разрезами, ориентированными по большому диаметру (365,4 Па) и аналогичной модели с (330,0 Па). Кроме того, объем тканей с высоким значением напряжения меньше у нашей модели (рис. 9-11). Особое внимание стоит уделить значению деформации. Предложенная нами модель демонстрирует большую способность деформироваться: значение deformation scale factor составляет +3,485е+03 (рис. 9). Значение этого же параметра для модели b составляет +3,461е+03 (рис. 10) и +3,355е+03 для модели c (рис. 11).

Рис. 9. Эпюра напряжений по Мизесу для предложенной модели (модель a)
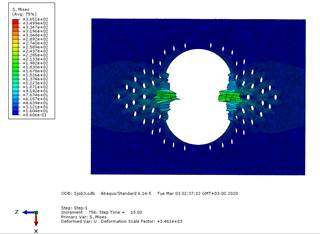
Рис. 10. Эпюра напряжений по Мизесу для модели с диаметрально ориентированными послабляющими разрезами (модель b)
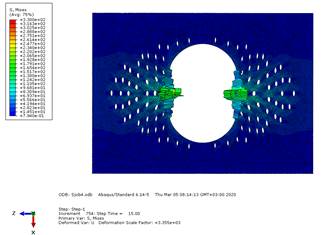
Рис. 11. Эпюра напряжений по Мизесу для модели с диаметрально ориентированными послабляющими разрезами (модель c)
Выводы
1. При небольших по размеру опухолях локальных стадий T1-T3 без отдаленного метастазирования, даже с прорастанием в подкожно-жировую клетчатку и кожу, в качестве up-front терапии необходимо проводить оперативный этап лечения. Небольшое количество рецидивов в исследуемой когорте женщин (11%) указывает на то, что большинство распадающихся опухолей могут быть удалены радикально.
2. Нанесение серии послабляющих разрезов является одним из оптимальных способов решения проблемы закрытия обширных дефектов кожи передней грудной стенки и заживления раны после перенесенной радикальной мастэктомии.
3. Предложенная математическая модель ориентации и расположения послабляющих разрезов позволяет, за счет большей способности к деформации, эффективно сводить края послеоперационного дефекта с меньшей вероятностью формирования зон повышенного натяжения кожи, что в конечном итоге будет способствовать лучшим условиям заживления раны и формирования оптимального косметического эффекта.
Библиографическая ссылка
Топузов Э.Э., Садыгова С.Н., Смирнов А.А., Трунин Е.М., Агишев Т.Т., Аршба Э.А., Татаркин В.В., Овсепьян А.Л., Щемеров Н.В., Остякова А.В. ОБОСНОВАНИЕ МЕТОДИКИ НАНЕСЕНИЯ ПОСЛАБЛЯЮЩИХ РАЗРЕЗОВ ДЛЯ ЗАМЕЩЕНИЯ ДЕФЕКТОВ КОЖИ ПОСЛЕ МАСТЭКТОМИИ У БОЛЬНЫХ РАСПАДАЮЩИМСЯ РАКОМ МОЛОЧНОЙ ЖЕЛЕЗЫ // Современные проблемы науки и образования. 2020. № 2. ;URL: https://science-education.ru/ru/article/view?id=29687 (дата обращения: 18.02.2026).
DOI: https://doi.org/10.17513/spno.29687



