В настоящее время исследователями не ставится под сомнение тезис о том, что математическая подготовка конкурентоспособных профессионалов аграрного профиля не только включает в себя формирование представлений о фундаментальных понятиях математики, но также должна быть ориентирована на применение математических знаний в будущей профессиональной деятельности студентов. При всем разнообразии предлагаемых подходов, моделей и концепций основным путем осуществления профильной направленности является применение в процессе обучения разнообразного дидактического инструментария, использующего системы традиционных и инновационных математических заданий, сформулированных в терминах специальных дисциплин. Профильная задача является важнейшим составным элементом таких систем заданий. Под профильной задачей будем понимать описание проблемной ситуации, в основе которой лежит процесс из будущей профессиональной деятельности студентов, а также всей аграрной сферы, решение которой достигается специальными математическими средствами и методами. При этом возрастает роль мотивационного фактора в обучении, поскольку студентам наглядно демонстрируется применение формализованных математических понятий в описании проблем и явлений окружающего мира.
Рассматривая профильную задачу как базовую единицу при составлении сложных дидактических конструкций, отметим важность ее грамотного использования в учебном процессе. В практике преподавания дисциплины «Математика и математическая статистика» у агробиологических направлений, таких как «Агрономия», «Агрохимия и почвоведение», «Ветеринария», «Садоводство», «Экология и природопользование», сталкиваемся с проблемой когнитивной трудоемкости таких заданий в связи с их усложненным понятийным аппаратом, что существенно затрудняет процесс понимания такого учебного материала. При этом нивелируется мотивационный эффект, увеличиваются временные затраты на решение.
Цель исследования: для осуществления профильно ориентированного обучения математике в аграрном вузе устранить указанные проблемы использования профильных задач путем поиска новых подходов, а также совершенствовать методы и приемы работы с такими задачами обращением к методологическим основам понимания учебных текстов.
Материал и методы исследования. В рамках указанной проблемы требуется исследовать процесс понимания профильных заданий – прежде всего учебных текстов сложной смысловой структуры, в которых синтезированы математическая задача и профильные термины. Пониманием будем считать как процесс постижения внутренних связей в содержании текста, так и процесс постижения смысла (или смыслов) текста. Кроме того, понимание - движение к знанию, производство знания (хотя и не само знание), а знание – это еще не понимание [1, с. 2]. В настоящей работе опирались на исследование «структуры понимания» применительно к процессу обучения математике в высшей школе, изложенной в [2].
В этой связи целесообразно обратиться к теоретическим принципам и методам философской, лингвистической и педагогической герменевтики как наук, изучающих интерпретации языковых выражений (текстов) и направленных на понимание смысла данных выражений [3]. Герменевтический подход при создании и применении учебных материалов в обучении математике активно используют в исследованиях [3, 4, 5]. Вслед за А.Г. Пригодиной в этом вопросе будем руководствоваться следующими принципами герменевтики: контекстуального подхода, разграничения смысла и значения, диалектической связи понимания и структуры языковых конструкций, диалогичности мышления, диалектического взаимодействия частей и целого [5, с. 2]. При этом воспользуемся:
1) методом движения по герменевтическому кругу;
2) методом выделения структуры текста;
3) методом аналогий при переходе от части к целому.
Результаты исследования и их обсуждение. Остановимся подробнее на первом методе. Герменевтическим кругом будем считать особенность процесса понимания, связанную с его циклическим характером, когда, ознакомившись с «целым», переходят к пониманию его частей, от них к «целому», т.е. мысль движется в своеобразном круге [4, с. 5]. В результате происходят лучшее осмысление «целого», его интеграция с частями. В контексте настоящего исследования это означает, что для понимания в целом профильной задачи необходимо понять ее отдельные части (словосочетания, термины), но для понимания отдельных частей уже необходимо иметь представление о математическом смысле целостной задачи. Отсюда следует, что обучаемый должен входить в герменевтический круг, уже имея первичные представления о соответствующем элементе знаний математической теории и его приложениях. Кроме того, следует актуализировать интерпретацию понятий профильных дисциплин, необходимых для решения профильной задачи.
В этом процессе понимание, а затем и смыслообразование учебного текста задачи достигаются через интерпретацию отдельных терминов, словосочетаний и предложений на язык математики путем построения математического выражения. Отметим, что герменевтический круг познания постоянно расширяется по мере включения в него частей целого. Подлинный смысл процесса понимания не сводится к замкнутой системе взаимодействия части и целого, так как познание предполагает расширение нашего понимания и постоянный выход за его пределы [4, с. 5]. Поэтому понимание и построение математической модели ситуации, описанной в задаче, будут достигнуты постепенно: по виткам герменевтического круга, неоднократно возвращаясь к более глубокому осознанию математической теории. Мы рекомендуем не останавливаться в движении по указанным траекториям познания, а расширять полученные смыслы в других профильных задачах с терминами другой области человеческой деятельности, используя метод аналогий.
Для организации процесса понимания по указанным траекториям требуется так структурировать содержание обучения, чтобы рассматривать в качестве частей и целого герменевтического круга связи и взаимодействия между математической теорией и ее отражением в аграрных практических задачах. При этом учебный материал системы прикладных профильных задач должен гармонично влиться в курс математики, сохранив системность, содержательную преемственность, доступность, целостность и внутреннюю логику курса.
В сфере оперирования описанными концепциями герменевтики предложено использовать линейно-концентрическую модель отбора содержания профильно ориентированного обучения. В данной модели базовой идеей служит положение о выделении инвариантного теоретического ядра курса и вариативных прикладных профильных оболочек [6, с. 10]. Разработанная на начальном этапе совместно с А.И. Архиповой, С.П. Грушевским данная модель получает свое развитие в различных направлениях, в частности в определении и уточнении структуры профильных оболочек.
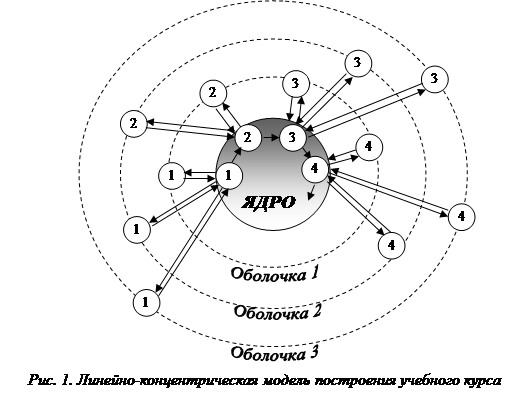
В модели содержательное инвариантное ядро представлено как совокупность основополагающих идей, законов, положений базового курса математики, отобранных в соответствии со стандартами образования и обеспечивающих ее систематическое и последовательное изучение. На основе фундаментального инвариантного ядра формируется содержание вариативных профильных оболочек, специальное для каждого направления обучения. Для аграрно-биологических направлений оболочки могут называться «Агрономия», «Экология», «Зоотехния». В них отдельные элементы математических знаний отражены в виде заданий, сформулированных в терминах будущей профессиональной деятельности студентов или моделирующих проблемную ситуацию из данной деятельности. Внешняя структура модели приведена на рисунке 1.
Здесь пронумерованными белыми окружностями обозначены элементы знаний теоретического ядра, которые присутствуют также в профильных оболочках. Стрелками показано разнообразие связей и отношений между элементами внутри модели. На рисунке взаимообратными стрелками представлено взаимодействие «целого» (фундаментальной математической теории) и частей (вариативных приложений математики) в герменевтическом круге, которое эксплинируется в виде взаимодействия отдельных элементов математических знаний и их применений в задачах сельского хозяйства.
Выстраивая предложенную систему связей как смысловой каркас текста задачи, а саму задачу встраивая в конструкцию построенного на основе линейно-концентрической модели курса математики, создаем четкую, целостную структуру – фундамент для интенсификации процесса понимания. Рассмотрим, как применить предложенное структурирование при решении следующей задачи, взятой из [7, с. 50].
Задача. Для некоторых сортов вики установлено, что при прочих равных условиях продуктивность (урожайность зеленой массы сена, семян) зависит от массы 1000 семян посевного материала. Если масса 1000 семян составляет 27,5 г, то урожайность зеленой массы составляет 150 ц/га и семян – 8 ц/га, а если масса 1000 зерен равна 42,5 г, то соответственно 225 ц/га и 15 ц/га. Считая, что графиком зависимости урожайности зеленой массы семян от массы 1000 семян на интервале от 22,7 до 42,5 является прямая, найти уравнение этих прямых и определить урожайность зеленой массы и сена при массе 1000 семян в 30 г.
Вышеизложенная задача громоздка и сложна для понимания, содержит много второстепенной уточняющей информации. Также в ней присутствуют «лишние» величины, не участвующие в решении, например «1000 семян». Для запуска процесса понимания обозначим здесь базовые математические понятия и связи с их приложениями. На рисунке 2 выделены задействованные в этой задаче элементы математических знаний ядра и их отражения в прикладных профильных оболочках. Так, в виде математической функции может быть представлена зависимость урожайности зеленой массы и семян от массы посевного материала. Здесь происходит расширение данного понятия в использовании его для описания явлений окружающего мира. В то же время через примеры использования в профессиональных ситуациях создаются условия для более глубокого понимания сути данного математического понятия. На рисунке 2 это отражено стрелками, обозначенными как «расширение понятия» и «углубление понятия». Проблемная ситуация задачи предполагает обращение к определенным математическим формулам, которые перестают для обучаемых казаться абстрактными и далекими от их профессиональной деятельности. Возникает следующий виток расширения применения понятия функции на практике, переходящий в углубленное понимание самого понятия. Выстраивается многократное обращение как к исходному математическому понятию и связанным с ним элементам знаний, так и к приложениям его в агрономии. Представленные на рисунке траектории движения мысли по герменевтическому кругу таким способом создают несколько витков.
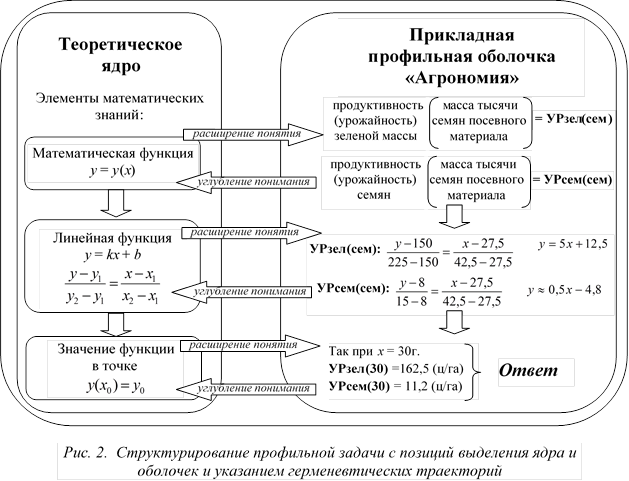
При работе вместе со студентами над текстом профильной задачи важно не столько преподнести данное структурирование в виде «готового знания», сколько создать предпосылки и условия для его самостоятельного составления. Обучаемый должен в тексте задачи увидеть предложенную структуру, записать основные соотношения кратко, в виде схемы. Так, в процессе работы над профильной задачей актуализируются разнообразные средства, методы и приемы для понимания учебного текста.
Особое место в этом процессе занимают технологии визуализации и сжатия (сгущения) информации, где задействованы высокоэффективные способы обработки и компоновки учебного материала [8, с. 12–18]. К ним можно отнести технику свертывания профильной учебной информации в укрупненную дидактическую единицу – функлистор. Данный термин произошел как эксплуатация зрительного образа функции и представляет собой введенные в стандартную запись функции ассоциативные символы (знак, слово, рисунок), имеющие смысловое значение для рассматриваемой ситуации из профильной дисциплины [9, с. 4]. На рисунке 2 функлистор представлен в упрощенном виде, как краткая запись зависимости продуктивности (урожайности) от массы семян. Разработки таких технологий визуализации и сжатия информации совместно со студентами при решении профильной задачи не только позволили представить учебный материал в доступном для понимания виде, но и способствовали его лучшему пониманию, развитию способности выделять главное, обобщать и систематизировать [10, с. 49].
Заключение. Процесс понимания профильной задачи неотделим от соответствующего структурирования ее учебного текста с применением герменевтического и профильно ориентированного подходов. В свою очередь такая задача встроена в структуру профильно ориентированного курса, созданного с применением этих же подходов. Умение увидеть и выделить отражения профильных понятий в математических конструкциях не только поможет в решении профильной задачи, но и запустит движение мысли по герменевтическому кругу, позволяя на более высоком уровне освоить фундаментальную математическую теорию, а также даст возможность обучаемым научиться обобщать, выделять главное, проводить аналогии, освоить методы компактного представления информации.
Предложенный подход к работе с профильными заданиями, включая и технологии визуализации и сжатия информации, активно применяется в Кубанском государственном аграрном университете имени И.Т. Трубилина [10] преподавателями кафедры «Высшая математика» на факультетах «Плодоовощеводство и виноградарство», «Агрономия», «Агрохимия и защита растений» для преподавания дисциплины «Математика и математическая статистка». В настоящее время на этих факультетах проводится заключительная стадия педагогического эксперимента, выявляющего аспекты использования предложенного в настоящей статье подхода в педагогической практике. Кроме того, открываются широкие перспективы использования предложенного структурирования не только в системе аграрного вуза, но и в общей дидактике высшего и профессионального образования, а также в создании разнообразного дидактического инструментария для реализации профильно ориентированного обучения. В этом направлении и будет продолжено данное исследование.
Библиографическая ссылка
Карманова А.В., Кондратенко Л.Н. ГЕРМЕНЕВТИЧЕСКИЙ ПОДХОД ПРИ ПРОФИЛЬНО ОРИЕНТИРОВАННОМ ОБУЧЕНИИ МАТЕМАТИКЕ В АГРАРНОМ УНИВЕРСИТЕТЕ // Современные проблемы науки и образования. 2020. № 1. ;URL: https://science-education.ru/ru/article/view?id=29570 (дата обращения: 20.02.2026).
DOI: https://doi.org/10.17513/spno.29570



