Интерактивное обучение (от англ. interation – «интеграция, взаимодействие») – обучение, построенное на взаимодействии учащегося с учебным окружением, учебной средой, которая служит областью осваиваемого опыта.
Термин «интерактивное обучение» (или «интерактивные технологии») появился относительно недавно. В начале 1990-х гг. его начали применять в отношении компьютерных технологий, в том числе электронного обучения. Существуют различные версии его появления. По мнению ряда авторов, данное определение произошло от термина «интерактивность», заимствованного из социологии, и концептуальной основой интерактивного обучения является теория интеракционистской ориентации (символического интеракционизма, ролевых теорий и теорий референтной группы), которая сформировалась в 1930-х гг. Основоположником символического интеракционизма является Дж. Мид. Люди не реагируют на внешний мир и других людей непосредственно, а осмысливают реальность в неких символах и соответственно продуцируют эти символы в ходе общения. Символический интеракционизм целиком основывается на интерпретациях человеческого поведения, в котором «прочитываются» значимые символы, несущие социальную информацию.
Существует также точка зрения, что интерактивное обучение появилось на основании термина «активное обучение» (Action Learning), который был предложен в 1930-х гг. английским ученым Регом Ревансом.
Применение интерактивного подхода к обучению в процессе реального, непосредственного общения субъектов образовательного процесса получило широкое распространение практически только после утверждения ФГОС-3, т.е. значительно позже разработок, осуществленных в рамках активного обучения. Видимо, поэтому в интерактивном обучении (ИО) используется весь арсенал наработок сторонников активного обучения (АО) – как в теоретических вопросах, так и в технологиях, а методы АО трактуются как интерактивные. Приведенная трактовка модели активного обучения при этом очевидным образом не совпадает с позицией сторонников активного обучения, которые рассматривали все виды взаимодействия субъектов образовательного процесса как необходимую составляющую активизации, а ограничения использования тех или иных видов общения могли быть связаны исключительно с дидактическими целями занятия [1, 2].
Следует уделить особое внимание содержанию некоторых инновационных методик интерактивного обучения. Одним из эффективных методов активации процесса обучения считается метод проблемного изложения. Другим эффективным методом инновационного обучения можно назвать метод кейс-стади, или метод учебных конкретных ситуаций (УКС) [3].
Авторами предлагается инновационный метод, основанный на использовании интерактивных учебных установок, имитирующих рассматриваемый физический процесс, с возможностью вариации входных параметров.
Отдельное место в интерактивном обучении занимает электронное обучение, которое наряду с дистанционными образовательными технологиями может применяться при реализации образовательных программ независимо от форм получения образования. В данном аспекте предложенная авторами методика интерактивного обучения естественным образом вписывается в контекст электронного образования и дистанционного обучения [4, 5].
Материалы и методы исследования
Для создания виртуальных учебных интерактивных экспериментальных установок, представляющих задачи повышенной сложности по физике, использовалась среда Macromedia Flash, включающая графический редактор и встроенный язык объектно-ориентированного программирования ActionScript 2.0. Достаточно подробная методология разработки приведена в работах [6, 7].
На первом этапе осуществлялось знакомство с физическими явлениями и реально существующими экспериментальными установками. Определялись необходимые приборы для функционирования установки. На втором этапе производилось решение прямой физической задачи, выяснялись необходимые переменные модели и предельные значения параметров величин. На базе решения прямой задачи находилось решение обратной задачи, при этом значение искомой величины задавалось с учетом погрешностей измерений и инструментальных погрешностей. На третьем этапе определялась структура интерфейса, производились разработка алгоритма и написание программного кода. На четвертом этапе осуществлялись тестирование программы и демонстрация физического процесса с заданием начальных условий экспериментальной задачи.
Результаты исследования и их обсуждение. Приведем примеры реализации метода интерактивного обучения с использованием авторских электронных установок при обучении решению задач по теории гармонических колебаний, которые вызывают у учащихся большие трудности, связанные с незнанием методики решения задач данного типа, которая заключается в обязательном использовании второго закона Ньютона для построения дифференциального уравнения гармонических колебаний указанной колебательной системы. Гармонические механические колебания происходят под действием квазиупругих сил, в качестве которой могут выступать все силы природы: тяжести, упругости, Архимеда, трения скольжения, Кулона, Ампера, Лоренца, давления, поверхностного натяжения, реакции опоры и другие [8, 9].
Примером колебаний, происходящих под действием силы тяжести, являются, например, колебания жидкости в сосудах U-образной формы.
На рисунке 1 представлена электронная экспериментальная установка, состоящая из сообщающихся сосудов U-образной формы, заполненных жидкостью с неизвестной плотностью r. Массу жидкости и диаметр сосудов можно задать с помощью соответствующих элементов на панели управления. Жидкость выводят из положения равновесия, и она начинает совершать гармонические колебания. Электронная установка имеет устройство управления, содержащее кнопки «Пуск», «Пауза» и «Сброс», которые выполняют интуитивно понятные функции. После нажатия на кнопку «Пуск» включается электронный секундомер и одновременно начинается процесс колебаний жидкости в сосудах. Количество совершенных колебаний фиксируется в отдельном поле. Таким образом, зная количество колебаний, совершенных за определенный промежуток времени, можно определить период колебаний. В задаче требуется найти плотность жидкости.
Рис. 1. Электронная установка экспериментальной задачи по изучению колебаний жидкости в сосудах U-образной формы
Для решения этой экспериментальной задачи воспользуемся вторым законом Ньютона. Если уровень жидкости в одном из колен сосудов сместить на элементарную величину x (например, повысить по отношению к первоначальному положению), тогда уровень жидкости в другом колене понизится на такую же величину. Поэтому разность уровней жидкости в сосудах будет равна 2x. В результате в том колене сосуда, в котором уровень жидкости будет выше, возникнет дополнительная неуравновешенная сила тяжести, равная весу жидкости, находящейся выше уровня жидкости в колене с меньшей высотой столба жидкости. Согласно второму закону Ньютона:
.
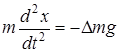Здесь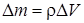 
– разность масс жидкости в обоих коленах в момент начала колебаний, 
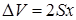– разность объемов, 
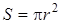– площадь поперечного сечения сосудов. С учетом этого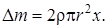 
Дифференциальное уравнение колебаний жидкости в сообщающихся сосудах U-образной формы будет иметь вид: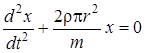 
.
Сравнивая полученное дифференциальное уравнение с известным дифференциальным уравнением гармонических механических колебаний, получим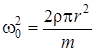 
.
Откуда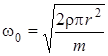 
, а период колебаний связан с циклической частотой согласно формуле 
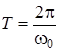и 
.
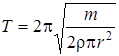Однако согласно определению периода колебаний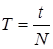 
. Время, за которое совершается определенное число колебаний жидкости, находится из виртуальной интерактивной установки. Приравнивая два последних выражения, можем найти искомую величину плотности неизвестной жидкости в виде:
.
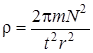Примером колебаний, происходящих под действием электростатической силы (силы Кулона), являются колебания заряженного тела в электрическом поле двух одноименно заряженных тел с одинаковым зарядом (рис. 2).
На краях гладкого стола длиной l жестко закреплены два тела с одинаковыми положительными зарядами q известной величины. Между этими зарядами посередине помещается бусинка массой m c положительным зарядом неизвестной величины Q. Установка позволяет изменять расстояние между зарядами (длину столика), их величину, а также массу бусинки. Если эту бусинку сместить из положения равновесия, то на нее будет действовать электростатическая сила, стремящаяся вернуть ее обратно. Колебания начинаются после нажатия на кнопку «Пуск» на блоке управления с одновременным включением секундомера. Таким способом экспериментально определяется период колебаний бусинки. Решение данной задачи аналогично решению предыдущей задачи и сводится к получению дифференциального уравнения колебаний бусинки и периода колебаний бусинк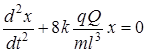и:
и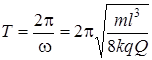 
.
Из последнего уравнения легко найти неизвестную величину задачи – заряд бусинки: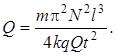 
Рис. 2. Электронная установка экспериментальной задачи по изучению заряженного тела в электрическом поле
На рисунке 3 представлена виртуальная интерактивная установка по моделированию колебаний стрежня, лежащего на двух вращающихся в противоположных направлениях блоках. Установка позволяет изменять расстояние между блоками, амплитуду колебаний и частоту вращения блоков. Колебания стержня возникают вследствие квазиупругой силы – силы трения. В задаче требуется найти коэффициент трения между стержнем и блоками. Задача сводится к построению дифференциального уравнения колебаний в виде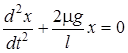 
, откуда 
.
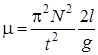Рис. 3. Электронная установка экспериментальной задачи по определению коэффициента трения методом вращающихся блоков
Заключение
Предложенная технология разработки интерактивных виртуальных установок ложится в основу разработки учебного окружения, учебной среды, которые в процессе изучения физики повышают эффективность процесса обучения, делают его более наглядным, насыщенным, способствуют развитию у обучающихся различных общеучебных умений, повышают качество обучения. Использование электронной демонстрации физического явления, к которой обучающиеся могут возвращаться несколько раз, меняя входные параметры, способствует более прочному и глубокому усвоению материала.
На основе представленных электронных установок можно создать обратные задачи повышенной сложности числом, равным количеству переменных модели экспериментальной задачи.
Создание образовательных сред для активного обучения, повышающих мотивацию учащихся, является неотъемлемой частью успеха в стратегии развития и внедрения интерактивного обучения.
Библиографическая ссылка
Девяткин Е.М., Хасанова С.Л. РЕАЛИЗАЦИЯ ИНТЕРАКТИВНОГО ОБУЧЕНИЯ ПРИ РЕШЕНИИ ФИЗИЧЕСКИХ ЗАДАЧ ПОВЫШЕННОЙ СЛОЖНОСТИ // Современные проблемы науки и образования. – 2019. – № 6. ;URL: https://science-education.ru/ru/article/view?id=29499 (дата обращения: 24.04.2024).