В последние годы происходят трансформации во всей системе высшего образования, в том числе и математического. Изменения направлены на усиление практической направленности образования, внедрение в образовательный процесс практических дисциплин, привлечение преподавателей, имеющих практический опыт в определенной профессии. Еще один аспект, связанный с изменением образования, предполагает сделать изучение учебных дисциплин личностно значимым для студента. В этом случае основная задача высшего образования – сделать общественно значимые ценности образования, в том числе и математического, личностно значимыми. Данный подход предполагает построение содержания образования таким образом, чтобы оно способствовало усвоению студентами информационной и методологической компонент образования. Учебная деятельность должна помогать моделированию творческой математической деятельности. В этом контексте математику следует рассматривать с позиции ее методологии и истории, а не как завершенную систему. Лишь при этом условии студенты будут осознавать необходимость математики и ее сущность. Очевидно, что решение этих задач невозможно без переосмысления всех составляющих системы обучения, куда входят цели, содержание, методы, а также формы и средства обучения (модели и технологии обучения) [1]. В данном исследовании проведены анализ и поиск путей повышения профессиональной заинтересованности, апробация различных методологических подходов к процессу преподавания математики для студентов технических специальностей. Целью работы стала проверка гипотезы о том, что применение в процессе обучения математике задач подобного характера влияет на эффективность усвоения студентами учебной информации.
Прикладная ориентация обучения высшей математике является одним из компонентов системы высшего образования. Она призвана развивать у студентов вузов элементы математической культуры, относящиеся ко всем этапам применения математических методов к решению прикладных задач. Прикладная ориентация играет значимую роль в создании у студентов мотивации и повышении интереса к предмету, осознании взаимосвязи математики с другими дисциплинами, а также с процессами, происходящими в реальной жизни. Для повышения прикладных навыков студентов необходимо на практических занятиях по высшей математике использовать такие приемы, как контроль и повышение правдоподобности решения, учет логических аспектов при решении прикладных и содержательных задач.
Прикладная направленность при обучении высшей математике не является новой методологической проблемой. Вопросы, связанные с изучением приложений математики, рассматривались в работах Ю.М. Колягина, А.И. Маркушевича, В.М. Монахова, А.В. Усовой, В.В. Фирсова и многих других авторов. Проблемы реализации прикладной ориентированности обучения математике нашли отражение в диссертационных работах Т.В. Малковой, С.С. Варданяна, Г. Трелиньски, В.А. Стукалова, В.Л. Самойлова и других авторов [2]. В этих исследованиях сформулированы принципы, которые обеспечивают прикладную ориентацию математики. Найдены конкретные решения в реализации прикладной направленности обучения в ходе изучения отдельных разделов математики. Следующую категорию составляют работы, анализирующие прикладные вопросы в процессе осуществления политехнического обучения и установления межпредметных связей между математикой и физикой (В.С. Самойлов, И.И. Блехман, А.Д. Мышкис, Я. Г. Пановко и др.) [3].
Психологические механизмы реализации прикладной направленности обосновываются в работах психологов Н.А. Мечинской, П.Я. Гальперина, Н.Ф. Талызиной, Ю.А. Самарина. В исследованиях этих авторов отмечается необходимость разработки методик, обеспечивающих при формировании умений активную деятельность самого обучаемого.
Но в методологическом и дидактическом плане решена лишь малая часть этой проблемы, и, несмотря на большое количество работ в этой области [4, 5], проблема реализации прикладной направленности высшей математики [6] до сих пор не нашла должного теоретического и особенно практического решения. Само понятие прикладной математики в математической и методической литературе, а также в практике обучения имеет весьма неопределенное содержание [7, 8]. Термин «приложения математики» употребляется и как синоним прикладной математики, и как процесс ее применения. Но это также не разъясняет ситуации, поскольку сами эти понятия не описаны достаточно точно и, как правило, понимаются по-разному.
Выделяют четыре основные точки зрения о роли прикладной математики в обучении: среди математических наук прикладная математика не является отдельной дисциплиной; прикладная математика – составная часть математики; прикладная математика – это особая дисциплина; прикладная математика выполняет роль языка в процессе применения математики.
Остановимся подробнее на различных точках зрения преподавания математики. Среди сторонников первой концепции нет согласия в вопросе, что включать в сферу математики. Часть исследователей утверждают, что к ней следует относить лишь чистые дедуктивные построения и все остальное математикой называться не должно. Другие, представляя математику живым организмом, настаивают, что сами по себе логические концепции составляют ее жесткий скелет, который делает ее устойчивой и достоверной. Но основные пути ее развития и продуктивность относятся в основном к ее приложениям, следовательно, математика без них – это как живой организм без мышц, нервов и сосудов. Сторонники третьей точки зрения считают, что математика не только охватывает дедуктивные области, но и включает все математические сущности – математические идеи и методы, объекты, встречающиеся не только в теоретической части математики, но и в ее приложениях: имеются в виду построение математических моделей, математический эксперимент, индукция и другие рассуждения математического характера. В этом случае возникают обширные области, в которых происходит сращивание математики с другими науками, так что отдельные фрагменты этих областей можно в равной степени отнести как к математике, так и к этим наукам. Исходной точкой для сторонников четвертой позиции является стремление отделить прикладную математику от приложений математики. Процесс применения математики охватывает три этапа: построение математической модели, исследование модели и интерпретацию результатов.
Для того, кто применяет математику, прикладная математика играет две роли: на этапе построения модели, а также при интерпретации полученного решения она исполняет роль языка, который предоставляет возможности выразить особенности данной ситуации [9, 10]. На этапе исследования модели она выступает в виде «чистой» математики с ее особенной методологией. Такой взгляд на прикладную математику позволяет сохранить правильное представление о собственном облике математики, высветляет ее методологию, создает возможность использования дедукции и эвристических методов, свойственных математической науке.
В педагогических работах [11, 12] под прикладной направленностью высшей математики понимают содержательную и методологическую взаимосвязь дисциплины с практикой, что предполагает овладение студентами компетенциями, необходимыми для решения практических задач средствами математики. В основе решения прикладных задач лежит математическое моделирование. Поэтому для осуществления прикладной направленности необходимо обучать студентов элементам моделирования [9, 13, 14], которыми с точки зрения дидактики являются учебные действия, выполняемые в ходе решения задач.
Математическая подготовка студента должна приводить к формированию у него математической культуры, относящейся к следующим трем этапам применения математики при решении практических задач: формализация (создается формальная математическая модель-задача), решение математической задачи и деформализация (интерпретация решения математической задачи, сопоставление этого решения с исходной проблемой). Происходят интерпретация решения математической задачи, сопоставление этого решения с исходной проблемой.
Исходная проблемная ситуация в схеме математического моделирования может быть абсолютно реальной или условной, конкретной или абстрактной, открытой с четко поставленным вопросом или только обозначенным контекстом. Ее содержательный анализ проводится с целью точнее осознать проблему и обдумать различные возможные отношения, связи, переменные, выявить существенные, уточнить термины, задуматься, хватит ли этих данных для решения проблемы. Эта фаза применения математики – фаза исследования ситуации.
Собранные знания о ситуации позволяют выделить с точки зрения решения проблемы переменные и существенные отношения между ними, то есть выявить структуру ситуации. Результат таких действий называется ситуационной моделью – физической, экономической и иной в зависимости от того, какой области принадлежит данная проблема. Эта модель, так же как и исходная проблемная ситуация, находится вне математики, но по отношению к исходной проблемной ситуации является ее схемой и одновременно конкретным предметом для дальнейших исследований. Описывая ее математическим языком (т.е. формализуя ее), мы получаем математическую модель исходной задачи. Математическая модель ситуации является уже математическим объектом, задачей, сформулированной только в терминах математики; следовательно, ее можно изучить математическими средствами. На практике модель M может быть уравнением, системой уравнений, функцией и т.д. Необходимо показать студенту, что можно строить различные модели, принимая всевозможные предпосылки, а также выбирая различные переменные, отношения и ограничения. Этот факт очень важен в обучении математике.
Этап математического решения проблемы наиболее полно и точно разработан в методических исследованиях (именно задачи такого характера имеют место в большинстве задачников для студентов). В результате исследования модели получается результат, который тоже является математическим объектом. Процесс интерпретации полученного решения (выражение в данном языке информации, представленной в ином языке) связывает два контекста: математический и действительный (ситуационный). На этом этапе может оказаться, что полученное решение не полностью соответствует (или совсем не соответствует) поставленной проблеме. В этом случае с учетом полученной информации модель уточняется (возможно, упрощается), и описанный процесс повторяется. Сопоставление результатов моделирования проводится на эмпирической основе, хотя часто возможна и теоретическая верификация, что с точки зрения математического образования весьма существенно.
Математическое моделирование само по себе имеет дидактическую ценность и выполняет определенные дидактические функции [13].
1. Познавательная. Методическая цель познавательная функции состоит в создании познавательного образа исследуемого объекта. Это формирование идет постоянно при переходе от простого к сложному. Например, при изучении кривых второго порядка совместно со студентами проводится поэтапное построение чертежа, при исследовании функции на монотонность (экстремум), выпуклость (точи перегиба) предваряют теоретическому обоснованию (построение аналитической модели) рассмотрение чертежа, на котором увязываются монотонность или экстремум функции с углами наклона касательных в соответствующих точках и далее со знаками (и значениями) производных в этих точках [14].
2. Управление деятельностью студентов. Математическое моделирование предметно и потому облегчает ориентировочные, контрольные и коммуникационные действия. Примером ориентировочного действия может служить построение блок-схемы исследования систем линейных уравнений. Контрольные действия способствуют обнаружению ошибок и могут выражаться в сравнении полученного решения одной задачи разными методами. Коммуникационная составляющая математического моделирования в большей степени необходима на этапах формализации и деформализации, где требуются перевод и сопоставление требований проблемной ситуации и полученного решения математической задачи.
3. Интерпретационная функция. Известно, что один и тот же объект можно выразить с помощью различных моделей. Например, прямую линию на плоскости можно задать различными способами: общим уравнением, с угловым коэффициентом, по точке и нормальному вектору, нормальным уравнением и иным способом, а также при помощи чертежа. Выбор определенного вида уравнения диктуется набором исходных данных. Чем значительнее вклад объекта в ситуационную модель, тем больше вариантов его представления желательно использовать.
4. Эстетическую функцию моделирования можно продемонстрировать, например, показывая на занятиях приложения математики в гуманитарных областях: живописи, архитектуре и т.д.
5. Функция моделирования способствует наиболее плодотворному мышлению студента, так как его внимание легко и своевременно переключается с модели на полученную с ее помощью информацию об объекте и обратно [10]. Такое переключение сводит к минимуму отвлечение умственных усилий студентов от предмета их деятельности.
Рассмотренные теоретические аспекты прикладной направленности обучения математике были положены нами в основу проведения педагогического эксперимента по включению задач с прикладным и профессиональным содержанием при проведении практических занятий по курсу «Высшая математика» со студентами филиала Самарского государственного университета путей сообщения в городе Нижнем Новгороде.
В качестве критерия эффективности усвоения рассматривался уровень усвоения информационной компоненты обучения. Показателями усвоения в данном исследовании выступали контрольные задания (тесты) с тремя уровнями сложности. Для проведения исследования были выбраны экспериментальные и контрольные группы. На практических занятиях в экспериментальных группах основное внимание уделялось решению задач прикладной и практической направленности. В контрольных группах занятия велись традиционными методами. Для достоверности исследования при проведении педагогического эксперимента было учтено требование репрезентативности выборки. Для качественной оценки знаний и умений по результатам теста использовались таблицы многомерного анализа результатов учебных достижений. Сводные результаты тестирования для экспериментальных и контрольных групп по каждому уровню усвоения учебного материала в контрольных и экспериментальных группах представлены на рисунке.
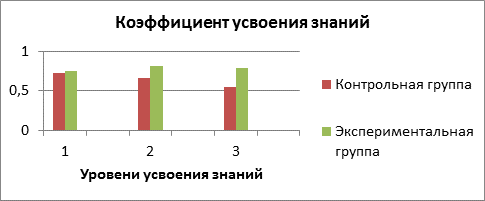
Сводные значения по коэффициенту усвоения знаний студентами технических специальностей
Как видно из рисунка 1, у экспериментальных групп эффективность процесса обучения, усвоение знаний и умений выше относительно контрольных групп, особенно это заметно на уровнях 2 и 3. На первом уровне различия между экспериментальной и контрольной группой находятся в пределах погрешности. На следующих уровнях эффективность экспериментальной группы существенно возрастает, что, вероятно, связано с интересом студентов и накоплением ими навыков решения задач. В контрольной группе эффективность падает по мере усложнения задач, что можно объяснить недостаточным уровнем знаний и навыков для решения подобных задач.
Выводы
На основе полученных в ходе исследования данных можно сформулировать следующие выводы: включение в практикум по курсу «Высшая математика» задач прикладной и профессиональной направленности оказало существенное влияние на эффективность усвоения студентами учебной информации. На основе полученных результатов доказана гипотеза о существовании зависимости между включением задач прикладной направленности при проведении практических занятий по математике и повышением уровня усвоения студентами учебной информации.
Библиографическая ссылка
Архаров Е.В., Катаева Л.Ю. О НЕКОТОРЫХ ТЕОРЕТИЧЕСКИХ АСПЕКТАХ ПРИКЛАДНОЙ НАПРАВЛЕННОСТИ ОБУЧЕНИЯ ВЫСШЕЙ МАТЕМАТИКЕ СТУДЕНТОВ // Современные проблемы науки и образования. 2019. № 6. ;URL: https://science-education.ru/ru/article/view?id=29433 (дата обращения: 17.02.2026).
DOI: https://doi.org/10.17513/spno.29433



