Профессиональная подготовка специалиста является актуальной проблемой высшего образования. Задача вуза – формирование личности, которая обладает общекультурными и профессиональными навыками, способностью к самостоятельному получению новых знаний, умений и навыков. Каждый предмет должен быть направлен на реализацию обозначенной выше задачи. Не составляет исключения и дисциплина «Математика и основы математической обработки информации» в учебном плане будущих учителей физической культуры [1]. Ведь многие процессы, явления, связанные со спортом, физической подготовкой, соревнованиями, а также в целом с педагогической деятельностью, можно описать на математическом языке с помощью уравнений, неравенств, систем уравнений, дифференциальных уравнений, графов и иного, проанализировать с помощью теоретико-множественных, вероятностных, статистических методов и сделать соответствующий вывод.
Цель исследования: показать на примерах, что знание основных способов математической обработки информации является важным аспектом профессиональной подготовки будущих учителей физической культуры.
Материал и методы исследования. В результате изучения дисциплины «Математика и основы математической обработки информации» формируется математический компонент профессиональной подготовки обучающегося [2]. Студент, освоивший данную дисциплину, должен:
· знать:
– основные разделы математики;
– основные методы математической обработки информации (теоретико-множественные, вероятностные, статистические);
· уметь:
– применять изученные методы при решении профессиональных задач;
– формулировать прикладные проблемы на языке уравнений, систем уравнений, неравенств, графических представлений;
– проводить практические расчеты по имеющимся экспериментальным данным при использовании статистических таблиц и компьютерной поддержки (включая пакеты прикладных программ);
– анализировать полученные результаты, формировать выводы и заключения;
· владеть:
– навыками применения методов математической обработки информации;
– математическим аппаратом обработки данных в области педагогики.
Решение обозначенных выше задач позволяет сформировать математический аспект готовности будущего учителя к профессиональной деятельности. А для этого необходимо включать в лекционные и практические занятия задачи, иллюстрирующие необходимость знания математических методов обработки информации для будущих учителей физической культуры [3]. Приведем примеры таких задач из различных разделов математики.
Начнем с задач, для решения которых применяются теоретико-множественные методы обработки информации.
Задача. В классе 25 учеников, из них 9 человек занимаются плаванием, 12 – спортивной гимнастикой, 15 – легкой атлетикой, 6 – плаванием и спортивной гимнастикой, 7 – плаванием и легкой атлетикой, 8 – спортивной гимнастикой и легкой атлетикой, 3 – всеми тремя видами спорта. Сколько учеников не занимаются ни одним видом спорта?
Решение. Пусть П – множество учеников, занимающихся плаванием, С – множество учеников, занимающихся спортивной гимнастикой, Л – множество учеников, занимающихся легкой атлетикой.
Тогда множество учеников, занимающихся хотя бы одним видом спорта: 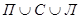 . Так как 9+12+15=36>25, значит, множества П, С, Л пересекаются. Следовательно, для ответа на поставленный вопрос применяем следующую формулу:
. Так как 9+12+15=36>25, значит, множества П, С, Л пересекаются. Следовательно, для ответа на поставленный вопрос применяем следующую формулу:
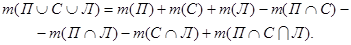
По условию задачи: 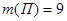 ,
, 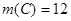 ,
, 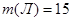 ,
, 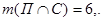
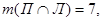
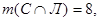
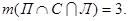 Подставляя эти значения в указанную выше формулу, получим:
Подставляя эти значения в указанную выше формулу, получим: 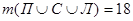 . Значит, ни одним видом спорта не занимаются 25 – 18=7 учеников.
. Значит, ни одним видом спорта не занимаются 25 – 18=7 учеников.
Ответ: 7 учеников.
Теперь рассмотрим задачи, для решения которых применяются комбинаторные методы обработки информации.
Задача. В классе 25 учеников, из которых 5 отличников, 11 хорошистов, 9 троечников. Необходимо выбрать группу для участия в спартакиаде, в которую бы входили 2 отличника, 3 хорошиста, 1 троечник. Сколькими способами это можно сделать?
Решение. Нам не важен порядок расположения учеников, поэтому для начала выберем двух отличников: это можно сделать 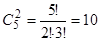 способами. Трех хорошистов можно выбрать
способами. Трех хорошистов можно выбрать 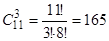 способами. Наконец, одного троечника можно выбрать
способами. Наконец, одного троечника можно выбрать 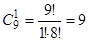 способами. Применяя теорему произведения для независимых событий, получим:
способами. Применяя теорему произведения для независимых событий, получим: 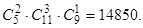 Таким образом, группу для спартакиады можно выбрать 14850 способами.
Таким образом, группу для спартакиады можно выбрать 14850 способами.
Ответ: 14850 способов.
Задача. В классе 15 учеников, которых необходимо направить на соревнования, включающие три вида спорта (на каждый вид спорта отправляется одинаковое количество учеников). Сколькими способами это можно сделать?
Решение. Учитывая, что нам не важен порядок попадания учеников в группу, то разделить их на три равные группы можно 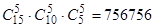 способами.
способами.
Ответ: 756756 способов.
Далее рассмотрим вероятностные методы обработки информации [4] для решения задач, связанных с работой учителя физической культуры.
Задача. В классе 20 учеников, среди которых 6 отличников. Для участия в тестировании случайным образом отбираются 5 человек. Какова вероятность того, что среди них окажутся 3 отличника, чтобы была уверенность в успешном прохождении тестирования?
Решение. Найдем вероятность того, что будут выбраны 3 отличника (обозначим это событие через А). Для этого из 6 отличников необходимо выбрать три человека, а из 14 учеников (не являющихся отличниками) выбираем 2 человека (так как группа должна состоять из пяти человек). Таким образом, получаем: 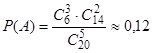 .
.
Ответ: 0,12.
Задача. Проводятся соревнования по ориентированию на местности. Команды состоят из двух человек. Каждому участнику дается индивидуальное задание, время на его выполнение – 60 минут. Выполнив задание, участник должен попасть в пункт B. Пришедший первым ждет другого в течение 20 минут, а затем, не дождавшись товарища по команде, вынужден продолжать соревнование уже в одиночестве. Найти вероятность встречи участников одной команды (время прихода каждого является независимой величиной).
Решение. Пусть А – искомое событие (встреча участников одной команды). Обозначим время прихода первого участника команды через t1, а второго – через t2. Для того чтобы встреча состоялась и они могли продолжить соревнования вдвоем, необходимо и достаточно, чтобы выполнялось следующее условие: 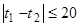 (так как пришедший первым ждет другого в течение 20 минут). Воспользуемся геометрическим определением вероятности. Для этого изобразим t1, t2 как координаты на плоскости. При этом всевозможные исходы изображаются точками квадрата со стороной 60 ед. (так как на выполнение задания дается 60 минут, за которые каждый из них должен попасть в пункт B). Искомая вероятность равна отношению площади фигуры F к площади квадрата (рис.). Для нахождения площади фигуры F вычтем из площади квадрата площади двух прямоугольных равновеликих треугольника, а именно:
(так как пришедший первым ждет другого в течение 20 минут). Воспользуемся геометрическим определением вероятности. Для этого изобразим t1, t2 как координаты на плоскости. При этом всевозможные исходы изображаются точками квадрата со стороной 60 ед. (так как на выполнение задания дается 60 минут, за которые каждый из них должен попасть в пункт B). Искомая вероятность равна отношению площади фигуры F к площади квадрата (рис.). Для нахождения площади фигуры F вычтем из площади квадрата площади двух прямоугольных равновеликих треугольника, а именно:

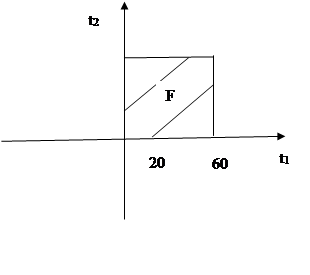
Таким образом, вероятность встречи двух участников одной команды, чтобы они могли вдвоем продолжить соревнования, приближенно равна 0,556.
Ответ: 0,556.
Наконец, рассмотрим задачи, для решения которых необходимо применение статистических методов обработки информации. Именно эти способы наиболее широко используются в работе педагога и, в частности, учителя физической культуры. Знание этих методов позволяет обрабатывать массивы данных [5], получаемых в ходе педагогических экспериментов (соревнования, сдача нормативов и т.д.), анализировать полученные результаты и делать соответствующие выводы (например, об успешности той или иной методике, о репрезентативности выборки и т.д.).
Задача. Дана последовательность значений результатов забега в одном классе (в минутах): 15; 20; 18; 20; 22; 15; 16; 20; 17; 23; 23; 23; 21; 22; 21; 23; 23; 22; 21; 19; 19; 22; 15; 16; 20. Определить, насколько результаты учеников отличаются от среднего значения времени забега.
Решение. Составим вариационный ряд:
|
Время забега хi (в минутах) |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
Количество учеников |
3 |
2 |
1 |
1 |
2 |
4 |
3 |
4 |
5 |
|
Вероятности |
0,12 |
0,08 |
0,04 |
0,04 |
0,08 |
0,16 |
0,12 |
0,16 |
0,2 |
1. Найдем математическое ожидание случайной величины х:
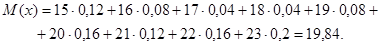 .
.
Таким образом, среднее значение времени забега равно 19,84.
2. Найдем математическое ожидание случайной величины х2:
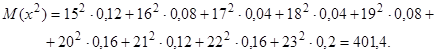 .
.
3. Вычислим дисперсию случайной величины х:
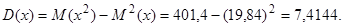
Как известно, чем больше дисперсия, тем больше рассеяны значения случайной величины вокруг ее среднего значения (математического ожидания). В нашем случае результаты соревнований отличаются от среднего значения незначительно.
Ответ. D(x)=7,4144.
Задача. В таблице представлены результаты соревнований по бегу, полученные в трех группах, занимающихся по трем разным методикам:
|
Группа |
Среднее время в группе, мин (xi) |
Численность группы, человек (ni) |
Дисперсия в группе (Di) |
|
Группа 1 |
62 |
23 |
10.15 |
|
Группа 2 |
59 |
25 |
9,81 |
|
Группа 3 |
71 |
18 |
12,3 |
Определим, насколько успешность выступления на соревнованиях зависит от выбора методики подготовки.
Решение
1. Найдем среднее время на соревнованиях для всех участников:
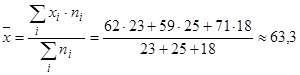 .
.
2. Вычислим внутригрупповую дисперсию:
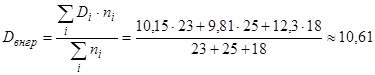 .
.
3. Вычислим межгрупповую дисперсию:
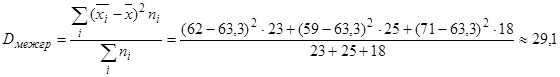 .
.
4. Найдем общую дисперсию:
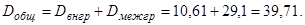
5. Найдем коэффициент детерминации, который и характеризует, насколько сильно результаты соревнований обусловлены выбором той или иной методики подготовки:
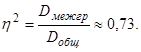
Полученный результат говорит о том, что успешность на соревнованиях по бегу на 73% обусловлена выбором той или иной методики подготовки.
Ответ: успешность на соревнованиях по бегу на 73% обусловлена выбором той или иной методики подготовки.
Задача. Для проведения соревнований по вольной борьбе необходимо, чтобы у участников из одной группы была примерно одинаковая масса тела. Взвешивание показало следующие результаты: 87, 93, 94, 95, 96, 88 кг. Можно ли проводить соревнования среди участников этой группы?
Решение.
1. Вычислим выборочную среднюю:
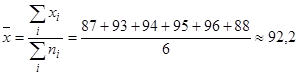 .
.
2. Вычислим ошибку репрезентативности выборочной средней:
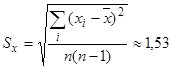 .
.
3. Вычислим коэффициент вариации:
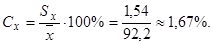
Принято считать, что различие между испытуемыми по некоторому признаку незначительно, если коэффициент вариации не выше 5%. Следовательно, в данном примере участники группы незначительно отличаются друг от друга по массе тела (так как коэффициент вариации равен 1,67%), и можно проводить соревнования среди участников этой группы.
Ответ: среди участников этой группы можно проводить соревнования.
Результаты исследования. Таким образом, на основании вышеизложенного можно сделать вывод о том, что, помимо формирования общей математической культуры студента, развития аналитического мышления, необходимого и в повседневной жизни любого человека, дисциплина «Математика и основы математической обработки информации» предоставляет инструменты (статистические ряды, критерии, формулы, алгоритмы и пр.), которые позволяют решать профессиональные задачи учителя физической культуры.
Вывод. Знание основных способов математической обработки информации является важным аспектом профессиональной подготовки будущих учителей физической культуры.
Библиографическая ссылка
Созонтова Е.А. ПРОФЕССИОНАЛЬНАЯ НАПРАВЛЕННОСТЬ КУРСА МАТЕМАТИКИ ПРИ ПОДГОТОВКЕ УЧИТЕЛЕЙ ФИЗИЧЕСКОЙ КУЛЬТУРЫ // Современные проблемы науки и образования. 2019. № 6. ;URL: https://science-education.ru/ru/article/view?id=29404 (дата обращения: 22.02.2026).



