Современное общество требует ускоренного совершенствования образовательного пространства, определения целей образования, учитывающих государственные, социальные и личностные потребности и интересы. Внедрение нового образовательного стандарта высшего образования для бакалавриата по направлению подготовки 44.03.05 Педагогическое образование (с двумя профилями подготовки), утвержденного Приказом Министерства образования и науки Российской Федерации от 22 февраля 2018 г. № 125, повлекло за собой ряд изменений в структуре и содержании примерной основной образовательной программы (ПООП). Кроме того, изменений требуют и условия реализации программ. Все это должно привести к качественным изменениям подготовки бакалавров. Внедрение в практику образовательных учреждений ФГОС ВО 3++ потребует от вузов дальнейшего совершенствования учебно-методических материалов, организации учебного процесса и повышения профессионального уровня профессорско-преподавательского состава [1].
Особенность нового поколения основных профессиональных образовательных программ высшего образования (ОПОП ВО) состоит в реализации идей компетентностного подхода, являющегося основой ФГОС ВО. Стандарт содержит универсальные, общепрофессиональные, профессиональные компетенции [2].
Предметная подготовка бакалавров – будущих учителей математики, направленная на формирование компетенций, может быть основана на концепции поликонтекстного образовательного модуля и реализована на основе дорожной карты. В контекстном обучении содержание заключено в комплексе учебных проблем и задач, близких к профессиональным, что способствует формированию профессиональных компетенций при изучении теоретических дисциплин [3]. Такой профессиональный модуль пронизывает все курсы обучения и стимулирует самостоятельную исследовательскую работу студентов.
Определение профессиональных компетенций осуществляется на основе профессионального стандарта педагога, а также требований к должности «Учитель». Преподавание учебного предмета «Математика» осуществляется в соответствии с требованиями Федерального закона «Об образовании в Российской Федерации» от 29 декабря 2012 г. № 273-ФЗ, ФГОС ООО и ФГОС СОО (приказы Минобрнауки № 1897 и № 413), «Концепцией развития математического образования в Российской Федерации» (Распоряжение Правительства Российской Федерации от 24 декабря 2003 г. № 2506-р.) [4]. Для решения проблем мотивационного характера, приведенных в Концепции, при обучении математике нужно опираться на практическую значимость нового материала, показывать возможность использования полученных знаний при решении профессиональных и жизненных задач. Кроме того, рекомендуется использовать трехуровневое обучение, чтобы предоставить учащимся возможность достижения своего уровня знания математики: «Математика для жизни», «Математика в профессии», «Научно-ориентированный уровень». Одной из задач профессиональной деятельности выпускников в области образования является организация научно-исследовательской и проектной работы учащихся в рамках предметной области.
В [2] выделены следующие актуальные проблемы высшего педагогического образования, решение которых является целью данной работы:
1) определение профессиональных компетенций с учетом профиля и специфики конкретной предметной (надпредметной) области;
2) поиск современных форм, методов и средств обучения, в условиях которых возможны эффективное формирование и оценка уровня сформированности указанных компетенций в процессе аудиторной и внеаудиторной самостоятельной работы обучающихся.
Материалы и методы исследования
В качестве решения первого вопроса творческим коллективом ЮУрГГПУ при разработке ПООП предложена обязательная профессиональная компетенция ПКО1: Способен осваивать и использовать базовые научно-теоретические знания и практические умения по предмету в профессиональной деятельности. Кроме того, сформулированы индикаторы ее достижения.
ПКО1.1 Знает содержание, особенности и современное состояние, понятия и категории, тенденции развития соответствующей профилю научной (предметной) области; закономерности, определяющие место предмета в общей картине мира; принципы проектирования и реализации общего и (или) дополнительного образования по профилю.
ПКО1.2 Умеет применять базовые научно-теоретические знания по предмету и методы исследования в предметной области; осуществляет отбор содержания, методов и технологий обучения предмету (предметной области) в различных формах организации образовательного процесса.
ПКО1.3. Владеет практическими навыками в предметной области, методами системного анализа базовых научно-теоретических представлений для решения профессиональных задач.
В формирование этой компетенции основной вклад вносит изучение студентами профильных математических дисциплин, в частности алгебры. Внедрение ФГОС ВО 3++ повлекло за собой корректировку учебных планов, которая в свою очередь привела к сокращению аудиторных часов более чем на 20%, в том числе и на профильные математические дисциплины. Таким образом, структура и содержание дисциплин требуют пересмотра, поиска новых подходов, форм и методов обучения, использования современных образовательных технологий.
Дисциплина «Алгебра» является основой предметной подготовки бакалавра, базой для изучения теории чисел, математической логики, дискретной математики, методики обучения математике и для подготовки к педагогической практике. Главная цель этого курса – помочь студентам изучить основные структуры алгебры, воспитать общую алгебраическую культуру, необходимую будущему учителю для глубокого понимания как основного школьного курса математики, так и школьных факультативных курсов. Данный курс читается студентам-математикам на протяжении четырех семестров и играет большую роль в фундаментальной подготовке будущего учителя в плане понимания сущности прикладной и практической направленности обучения математике наряду с математическим анализом [5] и геометрией.
Балльно-рейтинговая система [6] оценивания результатов освоения ОПОП позволяет реализовать на практике индивидуальный подход благодаря разноуровневым заданиям. Студенты в течение семестра оценивают свой уровень достижений, учатся рефлексии, самоорганизации при выполнении самостоятельной работы. Итоговая оценка на экзамене полноценно отражает аудиторную и самостоятельную работу в течение всего семестра. Промежуточная аттестация состоит из двух этапов: итоговой контрольной работы и экзамена (во втором, третьем и четвертом семестрах). Приведем пример контрольной работы второго семестра.
1) Указать пары матриц, которые можно сложить и которые можно перемножить:
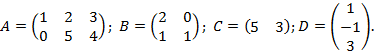
2) Решить систему уравнений и выполнить проверку. 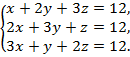
3) Вычислить 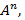 где
где 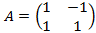 .
.
4) Предприятие выпускает три вида продукции, используя сырье трех типов. Характеристики производства указаны в матрице А, строки которой выражают расход определенного вида сырья по трем видам продукции, запасы производства указаны в матрице В. Определить объем выпуска продукции каждого вида при заданных запасах сырья. 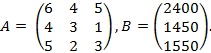
Укажем компоненты компетенции ПКО1, соответствующие задачам контрольной работы и позволяющие оценить уровень их сформированности, в таблице 1.
Таблица 1
Соответствие компонентов компетенции ПКО1 задачам контрольной работы
|
Задание |
Компоненты компетенции, проверяемые в задании |
|
1 |
Знает правила выполнений действий с матрицами (ПКО1.1). |
|
2 |
Знает и умеет применять методы решения систем линейных уравнений (ПКО1.1, ПКО1.2). Владеет вычислительными навыками (ПКО1.3). |
|
3 |
Знает правила выполнений действий с матрицами (ПКО1.1). Умеет умножать матрицы (ПКО1.2). Владеет основными законами логики, правилами записи математических рассуждений, навыками исследовательской деятельности (ПКО1.3). |
|
4 |
Знает и умеет применять методы решения систем линейных уравнений (ПКО1.1, ПКО1.2). Владеет культурой построения алгебраических моделей с целью решения экономических задач средствами алгебры (ПКО1.3). |
Результаты исследования и их обсуждение
Эффективное формирование выделенной компетенции при изучении дисциплины «Алгебра» возможно при реализации следующей структуры курса. Изучение дисциплины начинается во втором семестре, после освоения «Вводного курса математики» и «Элементарной математики». Здесь происходит знакомство с линейной алгеброй: рассматриваются методы решения систем линейных уравнений, понятия линейного векторного пространства и линейной зависимости, пространство матриц и их свойства, теория определителей. Эти разделы сравнительно легко усваиваются студентами, многие задачи здесь носят вычислительный характер, имеют четкий алгоритм решения. Кроме того, матрицы и определители имеют прикладное значение в экономике, информатике и других отраслях. Однако большой объем вычислений вызывает серьезные затруднения у студентов с несформированными вычислительными навыками. В такой ситуации полезно закрепить теоретический материал на учебной практике (ознакомительная практика по математике).
Материал этого семестра может быть использован при руководстве научными проектами школьников в профессиональной деятельности выпускника (обучение математике на третьем уровне). Например, темы проектов могут быть связаны с линейным программированием (это и выход на экономические приложения, и реализация алгоритмов в различных языках программирования), с описанием экономических зависимостей.
Третий семестр состоит из двух разделов. В первом продолжается изучение линейной алгебры: рассматриваются линейные отображения векторных пространств, а также пространства со скалярным произведением. Во втором разделе углубляются знания о группах и кольцах, студенты приближаются к современной алгебре, дисциплина становится все более абстрактной, ее изучение вызывает трудности у студентов, прикладное значение этих разделов не очевидно для них. В [7] отмечено, что аксиоматический подход к построению раздела и учебники, рассчитанный на подготовленного читателя, усложняет усвоение студентами идей современной алгебры. Однако руководство учебно-исследовательской деятельностью обучающихся является профессиональной компетенцией учителя математики, и ее формирование зависит от знания и понимания основ современной математики.
В следующем, четвертом, семестре рассматривается теория многочленов от одной и нескольких переменных, а также уточняются особенности полиномов над числовыми полями и кольцом целых чисел. Завершается курс алгебры в пятом семестре изучением теории расширений полей. Элементы теории многочленов и поиска их корней входят в программу школьного курса алгебры и необходимы учителю для подготовки школьников к успешной сдаче Единого государственного экзамена по математике на профильном уровне. Кроме того, эта теория имеет важное прикладное значение в сфере криптографии и теоретических основ информатики и может быть основой для руководства научно-исследовательской деятельностью школьников.
Освоение абстрактных понятий алгебры позволяет быть исполнителями в проектах по тематике, близкой современным научным исследованиям: построение таблиц характеров конечных групп [8], описание групповых колец и поиск их обратимых элементов, изучение гиперкомплексных чисел. Такие проекты предполагается реализовать в ходе учебной практики (проектно-исследовательской работы), предусмотренной в учебном плане в шестом семестре после завершения изучения профильных математических дисциплин «Алгебра», «Геометрия», «Математический анализ». Важным инструментом для реализации исследовательских проектов служат пакеты математических вычислений, такие как GeoGebra [9], Desmos, MathCad, Matlab, GAP, знакомство с которыми происходит на учебной практике (по профилю) в четвертом семестре. В ходе этой практики студенты также учатся грамотному оформлению математических текстов со сложными формулами, таблицами, чертежами в различных текстовых редакторах и издательских системах.
При понимании принципов и основ научных идей современный учитель имеет возможность для расширения своего кругозора, использования межпредметных связей, осуществления интеграции знаний между различными школьными дисциплинами [10]. В процессе профессиональной деятельности межпредметные связи помогают выполнять задачи, поставленные перед учителем.
Выводы
С целью формирования профессиональных компетентностей будущих учителей математики необходимо использовать различные методы и способы обучения бакалавров направления подготовки Педагогическое образование: поликонтекстные образовательные модули и практико-ориентированные задачи, балльно-рейтинговую систему оценивания результатов обучения, выполнение индивидуальных или групповых проектов по междисциплинарной тематике или в рамках одной учебной дисциплины, учебных мини-проектов. Также этому способствуют организация научно-исследовательской работы бакалавров на протяжении всего времени обучения с представлением результатов такой работы на студенческих конференциях, участие в конкурсах студенческих научных работ и проектов, своевременная актуализация содержания дисциплин с тщательным подбором материала, отбором содержания аудиторных занятий и эффективно организованной самостоятельной работой студентов.
Работа выполнена при финансовой поддержке ФГБОУ ВО «Шадринский государственный педагогический университет» по договору о выполнении НИР № 16-382 от 28.05.2019.
Библиографическая ссылка
Шумакова Е.О., Севостьянова С.А., Вагина М.Ю. ФОРМИРОВАНИЕ ПРОФЕССИОНАЛЬНЫХ КОМПЕТЕНЦИЙ БАКАЛАВРОВ ПРИ ИЗУЧЕНИИ ДИСЦИПЛИНЫ «АЛГЕБРА» // Современные проблемы науки и образования. 2019. № 5. ;URL: https://science-education.ru/ru/article/view?id=29223 (дата обращения: 03.03.2026).



