Завершение перехода Российской Федерации к рыночной экономической системе обеспечивает необходимость перехода от системы массового образования, характерной для индустриальной экономики, к непрерывному индивидуализированному образованию для всех, к развитию образования, связанного с мировой и отечественной фундаментальной наукой, ориентированного на формирование творческой социально ответственной личности [1].
Основной характеристикой современной парадигмы образования становится переход к концепции личностно центрированного образования. Такая концепция способствует включению механизмов саморазвития личности, раскрытию творческих способностей и созданию условий для самореализации.
В связи с этим ведущим направлением деятельности современного образования становится повышение конкурентной способности выпускника российской системы образования на национальном и мировом уровне, а основной задачей – подготовка разносторонней, творческой личности с развитыми индивидуальными способностями. Современный специалист должен обладать не только глубокими знаниями и компетенциями, но и быть способным постоянно их обновлять, самообразовываться, уметь оперативно находить и квалифицированно использовать нужную информацию, в том числе с использованием информационных технологий.
Нацеленность образования на становление и развитие личности обуславливает качественно новый подход к организации образовательного процесса – проектно-целевой.
Цель данной статьи заключается в описании одного из возможных средств обучения математике на основе проектно-целевого подхода, обеспечивающего возможность каждому студенту выстраивать свой маршрут изучения дисциплины, выбирать подходящий контент для удовлетворения личностных потребностей и предпочтений, а также форму представления учебного материала. Основная идея работы – разработка курса-трансформера для изучения математики студентами технического вуза, обеспечивающего повышение их уровня математической компетентности за счет инновационной организации учебного процесса.
Федеральная целевая программа развития образования на 2016–2020 гг. предусматривает проектно-целевой подход ее реализации. Под проектно-целевым подходом понимается общая методология распределения ресурсов на достижение комплекса конкретных целей для каждой подзадачи, на которые разбита решаемая проблема. Достижение каждой цели при этом имеет измеримые показатели (индикаторы).
Методологические основы проектно-целевого подхода пока еще формируются в виде научной теории. Однако исследователи сходятся в одном: его реализация предполагает рассмотрение целей, содержания и технологий обучения как «проект инновационной деятельности на интегративной основе» [2]. Следовательно, в качестве основных компонентов данного подхода при обучении математике можно выделить целевой, содержательный и технологический.
Содержание математического курса строится преподавателем на основе ГОС ВО. Основное внимание при его проектировании уделяется постановке целей, учитывающих потребности студента, образовательного стандарта и рынка труда.
Проектирование технологического компонента нацелено на формирование у обучаемых мотивации к самообразованию, повышению уровня профессиональной компетентности, на интеграцию форм и методов обучения с учетом психофизиологических особенностей студентов.
Решение этих задач возможно при организации образовательного процесса на основе личностно центрированной концепции.
Личностно центрированный (personcentered) подход к обучению был разработан представителем американской гуманистической психологии К. Роджерсом [3]. Его суть заключается в необходимости использования «центрированных на личности» обучаемого форм и методов обучения.
Анализ научно-педагогической литературы российских ученых показал, что нередко термин «личностно центрированное» подменяется термином «личностно ориентированное обучение» [4]. Тем не менее каждое из этих понятий демонстрирует свое представление о построении образовательного процесса.
С точки зрения личностно ориентированного подхода студент - это не субъект педагогического воздействия, а его объект. Основная задача преподавателя в этом случае заключается в изучении личностных возможностей каждого студента и планировании его будущей деятельности.
В личностно центрированном же обучении процесс строится вокруг личности, происходит равноправный диалог преподавателя с обучаемым. При таком подходе студенты сами выбирают не только чему учиться, но также - как и почему. Основой такой среды обучения является сознательность обучаемого и его деятельность, в отличие от акцента на контроль преподавателя и освещение академического содержания, присущего традиционному обучению. Основная задача педагога заключается в обеспечении взаимодействия, центрированного вокруг личности обучаемого, а не в том, чтобы дать указания, наделить знаниями или навыками.
Поэтому возникает необходимость в учете индивидуальных особенностей студентов (разница уровней подготовки студентов к восприятию учебного материала); в характере индивидуальной самостоятельной деятельности; в способах восприятия и передачи информации и мышлении.
Теоретическим основам личностно центрированного подхода посвящены работы многих исследователей [5-7].
Однако методика обучения на основе личностно центрированного подхода разработана еще не достаточно. Очевидно, что главное место должны занимать проектные, исследовательские, дискуссионные способы организации учебной деятельности. То есть основными методами и средствами обучения должны быть те, которые обеспечивают возможность более самостоятельного и ответственного обучения: проект, исследование, взаимообучение, групповая работа, самооценка. Традиционные лекции следует заменить на самостоятельное изучение теоретического материала.
Поэтому вопрос модернизации учебно-методической литературы, разработки новых дидактических подходов к организации самостоятельной работы студентов, внедрения новых инновационных технологий и когнитивных средств и методов обучения становится жизненно необходимым.
Материал и методы исследования
С опорой на основные положения личностно центрированного подхода в данной работе описывается предложенный курс-трансформер по математике, обеспечивающий учет личностных характеристик и потребностей студентов за счет модульной организации учебного контента дисциплины, возможности выбора одного из предложенных нелинейных подходов к изучению модулей, применения метода проектов, использования интерактивных цифровых ресурсов и обучающих средств, учитывающих психофизиологические особенности восприятия информации и мышления.
Под модульной организацией учебного контента понимается представление содержания дисциплины в виде информационных блоков, усвоение которых осуществляется в соответствии с дидактической целью. Дидактическая цель каждого модуля содержит в себе не только указание на объем изучаемого содержания, но и на уровень его усвоения. Таким образом, студент получает возможность самопланирования учебного процесса и самоконтроля, выбора уровня изучения каждого модуля и соответствующих интерактивных цифровых ресурсов и обучающих средств в соответствии с личными особенностями восприятия информации и мышления.
Реализация модульной организации образовательного процесса обусловливает необходимость применения нелинейных технологий обучения. Под нелинейными технологиями обучения понимаются такие методы и способы непоследовательного обучения, которые предполагают изучение курса на интуитивном уровне познания, методом проб и ошибок [8].
Анализ литературы и собственного опыта показал, что к наиболее эффективным нелинейным подходам к обучению математике относятся проектный, концентрический, параллельный и когнитивный.
Под проектом (от латинского projectus – выдвинутый вперед) понимается реалистический замысел о желаемом будущем. Суть проектного подхода заключается в том, что он содержит в себе рациональное обоснование и конкретный способ (технологию) своей практической реализации. Одним из главных отличий применения данного подхода в настоящее время является его целевая направленность на что-то оригинальное, новое, неизвестное ранее. При таком подходе основной задачей преподавателя становится организация познавательной деятельности студентов, обучение учиться самостоятельно.
Концентрический подход предполагает ступенчатое, многоуровневое построение процесса обучения заданному курсу. Первый этап заключается в представлении всего курса на общем понятийном уровне. Наиболее эффективным здесь методом обучения будет метод системной динамики. Второй этап – базовый, на котором студенты получают базовые знания. Следующий уровень – исследовательский. Он требует освоения знаний на теоретико-логическом уровне.
Параллельный подход тесно связан с проектным, т.к. предусматривает параллельное изучение разных тем теоретического материала курса математики для решения одной комплексной задачи (проекта). Изучение курса будет более результативным, если разбить учебную группу на подгруппы, каждая из которых решает свою мини-задачу, выделенную в рамках проекта.
Когнитивный метод обучения опирается на основные положения когнитивной психологии и предполагает учет разных индивидуальных когнитивных особенностей в восприятии информации и мышлении. Наиболее эффективным средством обучения в данном подходе являются ментальные карты [9].
В работах [10; 11] представлена методическая система электронного курса- трансформера по информатике, обеспечивающего реализацию проектно-целевого подхода к обучению на основе личностно центрированной концепции.
В данной работе разработана методическая система курса-трансформера по математике для студентов технического вуза.
Практическая часть
С опорой на основы проектно-целевого подхода и личностно центрированной концепции обучения содержание курса-трансформера построено в модульной форме. Каждому модулю прописаны соответствующие цели и ожидаемые результаты обучения. Это дает возможность студенту построить свою индивидуальную траекторию изучения математики.
Изучение теоретического материала организовано как решение поставленной задачи в форме проекта. Проект может выполняться как индивидуально, так и в мини-группах по два-три человека.
В качестве примера рассмотрим курс-трансформер по математике для студентов технического вуза направления 29.03.04 «Технологии художественной обработки материалов». В соответствии с учебным планом и рабочей программой дисциплины содержание курса разбито на 6 модулей (рисунок 1):
- линейная алгебра (М1);
- векторная алгебра и аналитическая геометрия (М2);
- дифференциальное исчисление (М3);
- интегральное исчисление (М4);
- обыкновенные дифференциальные уравнения (М5);
- теория вероятностей и математическая статистика (М6).

Рис. 1. Модульная структура курса
Для каждого модуля определены цели изучения и ожидаемые результаты. Например, к основным целям изучения модуля 1 относятся формирование у студентов представлений об основных понятиях и методах расчета данных разделов математики и развитие навыков их практического использования при решении учебно-профессиональных задач; развитие логического и алгоритмического мышления.
Планируемые результаты – способность оперативно определять и применять методы линейной алгебры и теории комплексных чисел для решения конкретной задачи в профессиональной деятельности.
Для учета личностных психофизиологических особенностей восприятия информации и мышления студентов содержание каждого модуля представлено с использованием традиционной методики и описанных выше нелинейных технологий обучения математике: концентрической, параллельной и когнитивной (рисунок 2).
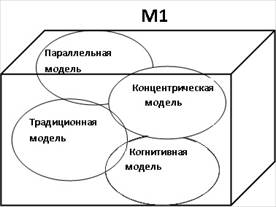
Рис. 2. Пример структурной модели Модуля 1
Опишем суть изучения математики с помощью различных технологий обучения на примере Модуля 1. В таблице приведено содержание первого модуля.
Содержание Модуля 1
|
Модуль 1. Линейная алгебра |
|
1.1. Понятие матрицы. Классификация матриц. Свойства матрицы. Действия над матрицами. |
|
1.2. Понятие определителя. Свойства определителей. Вычисление определителей разных порядков. Понятие обратной матрицы. Вычисление обратной матрицы. |
|
1.3. Понятие системы линейных алгебраических уравнений (СЛАУ). Понятие решения СЛАУ. Классификация СЛАУ. Методы решения СЛАУ. |
При традиционной модели обучения математике изучение теоретического материала происходит последовательно в соответствии с выписанным содержанием.
Концентрический подход предполагает изучение материала курса с выделением нескольких уровней (концернов), например понятийного, базового и исследовательского.
На первом (понятийном) уровне студент знакомится с основными понятиями линейной алгебры (матрица, определитель, СЛАУ и т.п.). Цель изучения данного уровня математического раздела заключается в формировании представлений об основных понятиях линейной алгебры. Результат изучения – способность корректного употребления понятий и символов линейной алгебры для выражения количественных и качественных отношений. Для проведения контроля достигнутых результатов создан соответствующий банк тестов.
Базовый уровень нацелен на знакомство с основными методами расчетов линейной алгебры. Результат обучения заключается в сформированности способности демонстрировать базовые знания линейной алгебры и готовности использовать их в профессиональной деятельности.
Исследовательский уровень предполагает более глубокое изучение основ линейной алгебры, в результате которого у студента формируется способность проводить анализ и использовать наиболее эффективный метод для решения аналитических и исследовательских задач профессиональной области.
При параллельном подходе студентам предлагается выполнить проект, требующий решение реальной задачи из профессиональной области. Группа разбивается на подгруппы, каждая из которых решает свою мини-задачу. В этом случае весь материал изучается параллельно.
Приведем пример такого проекта.
Тема проекта. Исследование режимов протекания заданной каталитической реакции:
1) 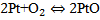 , 2)
, 2) 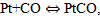 3)
3) 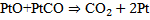 .
.
Данный проект выполняется в течение изучения всего курса математики. В рамках раздела «Линейная алгебра» студентам дается готовая математическая модель:
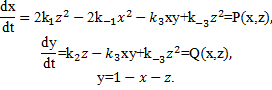
Их задача – исследовать стационарные состояния заданной химической реакции. Для этого им необходимо изучить основные понятия линейной алгебры, методы вычислений и решить СЛАУ:
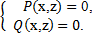
Когнитивный подход подразумевает представление теоретического материала курса в виде краткого справочника, оформленного с использованием интерактивных цифровых ресурсов и обучающих средств, таких как флеш-карточки, ментальные карты и т.п. На рисунке 3 представлена ментальная карта по линейной алгебре.
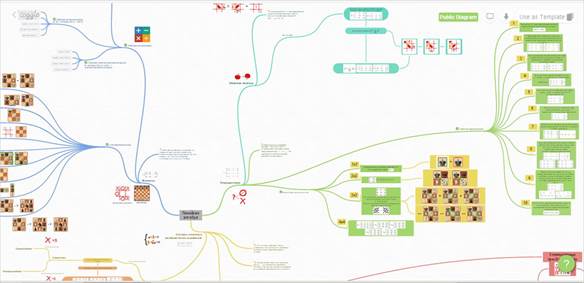
Рис. 3. Ментальная карта по линейной алгебре
Заключение
Задача формирования и развития реальной профессиональной компетентности современного выпускника как личности, способной к самообразованию и конкурентоспособности на рынке труда, обусловила необходимость разработки нового подхода к образованию – проектно-целевого. Проектно-целевой подход рассматривает цели, содержание, технологии образования как проект инновационной деятельности на интегративной основе. Для его реализации требуется пересмотр всех его компонент с позиции ожидаемых результатов обучения, в том числе математике, и построение соответствующего учебно-методического обеспечения. Построение курса-трансформера по математике на основе личностно центрированной концепции с использованием модульной организации содержания курса математики, нелинейных технологий обучения позволяет реализовать основные принципы данного подхода.
Методическая система курса-трансформера может быть рекомендована для создания подобных курсов при обучении другим дисциплинам.
Библиографическая ссылка
Пушкарева Т.П., Калитина В.В. О ФОРМИРОВАНИИ МАТЕМАТИЧЕСКОЙ КОМПЕТЕНТНОСТИ СТУДЕНТОВ НА ОСНОВЕ ПРОЕКТНО-ЦЕЛЕВОГО ПОДХОДА // Современные проблемы науки и образования. 2019. № 4. ;URL: https://science-education.ru/ru/article/view?id=29081 (дата обращения: 16.02.2026).



