В настоящее время, с развитием информационных технологий, байесовские методы нашли широкое применение в теории и практике эконометрических исследований и включены в учебные программы магистерской подготовки ведущих университетов в качестве дисциплин по выбору, основное назначение которых - дать представление о современных подходах байесовского оценивания и методах их реализации в статистических пакетах прикладных программ.
В байесовском подходе оптимальным образом используется информация из двух источников: априорная информация о моделируемом объекте (информация, полученная из предыдущих исследований или теоретических предположений) и статистическая информация, содержащаяся в результатах наблюдений. Обновленная информация (апостериорная вероятность) - результат применения формулы Байеса:
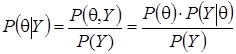, (1)
для непрерывных случайных переменных: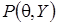 
- совместная функция плотности распределения вероятностей для вектора случайных наблюдений 
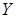и случайного вектора параметров 
,
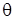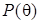- плотность априорного распределения, 
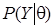- функция распределения плотности вероятностей для наблюдений Y при определенном векторе 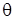(функция правдоподобия),
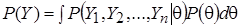
- полная вероятность, выполняющая роль нормирующего множителя и не зависящая от вектора параметров, поэтому формулу «обновления» (1) записывают в виде
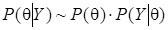, (2)
где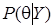 
- апостериорная функция плотности вероятности (ФПВ), включающая как априорную (через априорную плотность распределения вектора параметров), так и выборочную (через функцию правдоподобия) информацию, символ ~ знак пропорциональности. Полученную апостериорную ФПВ можно охарактеризовать мерами центральной тенденции (математическим ожиданием или модой), дисперсии и скошенности.
Основное преимущество применения байесовского подхода в его унифицированности, вне зависимости от типа моделей, и включает следующие этапы: выбор стохастической модели, генерирующей наблюдения; формулировка априорных допущений относительно значений параметров; формирование выборки; информация об апостериорной ФПВ и её обобщающих характеристиках (меры центральной тенденции и дисперсии, апостериорные интервалы). Байесовские методы имеют точностные преимущества по сравнению с классическими в условиях малых выборок, что характерно для эконометрических данных.
Работа нацелена на апробацию алгоритмов байесовского метода оценивания в рамках аналитического и численного МСМС-подхода, с выполнением оценивания и диагностики предпосылок метода в программной среде R.
Результаты исследования и их обсуждение. Процедура байесовского оценивания применима к широкому спектру моделей, рассматриваемых в рамках дисциплин эконометрического блока: регрессионных моделей, моделей с дискретной зависимой переменной, моделей временных рядов, систем одновременных уравнений, моделей для панельных данных. Программы дисциплин байесовского подхода в эконометрике, как правило, включают байесовский анализ классической модели линейной регрессии и байесовский подход с применением метода Монте-Карло по схеме Марковской цепи.
Выбор априорного распределения, задающего начальное представление о поведении параметров модели, базируется на семействе сопряженных распределений, для которых априорное и апостериорное распределения принадлежат одному и тому же семейству распределений.
Для существования сопряженного семейства априорных распределений функция правдоподобия должна быть представлена в виде произведения достаточных статистик:
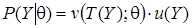, (3)
где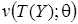 
- неотрицательная функция, зависящая от Y только через 
, 
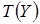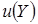- положительная функция от выборочных данных, не зависящая от параметров [1].
Для формирования семейства распределений, сопряжённого с наблюдаемой генеральной совокупностью, в случае представления функции правдоподобия в виде произведения (3) достаточно одного перехода. При этом в качестве априорных распределений при решении практических задач применяют два вида функций [2]:
для параметров, принимающих как положительные, так и отрицательные значения на числовой оси, априорная функция плотности принимает постоянное значение
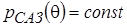, (4)
и поскольку в данном случае в функции (4) нет никакой информации о параметрах модели, в обозначении используется индекс САЗ - скудность априорных знаний;
для параметров, принимающих только положительные значения на числовой оси
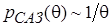, (5)
где 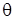случайный параметр. Таким образом, для построения семейства априорных распределений, сопряженных с наблюдаемой генеральной совокупностью, необходимо проверить возможность представления функции правдоподобия в виде произведения достаточных статистик и в зависимости от знаков параметров модели выбрать САЗ-апостериорное распределение:
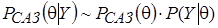. (6)
В байесовских моделях эконометрики в качестве элементов вектора 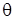включают вектор параметров моделей, дисперсии возмущений, автоковариационные матрицы возмущений и оценок параметров. Оценим модель множественной линейной регрессии байесовским методом:
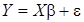. (7)
В (7) используются традиционные обозначения: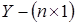 
- вектор значений эндогенной переменной, 
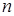- число наблюдений, 
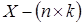- матрица регрессоров, 
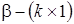- вектор параметров модели, 
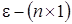- вектор возмущений, имеющий нормальное распределение 
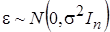, с числовыми характеристиками: математическое ожидание
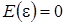, автоковариационная матрица 
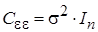, где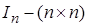 
- единичная матрица,
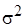- дисперсия случайного возмущения, 
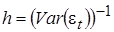- параметр точности (precision metrics).
Вектор эндогенных переменных модели также имеет нормальное распределение
,
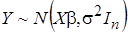с числовыми характеристиками: математическое ожидание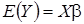
, автоковариационная матрица 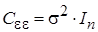, и плотностью распределения:
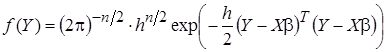. (8)
Можно показать, что достаточной статистикой плотности распределения функции (8) является функция, которая зависит от произведений матрицы регрессоров и вектора значений эндогенной переменной модели множественной линейной регрессии (7):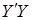 
, 
, 
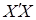. Это значительно упрощает процедуру оценивания неизвестных параметров модел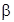и 
и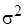
в рамках байесовского подхода, т.к. приводит к выполнению условия (3).
Для представления плотности (8) через оценки параметров модели и дисперсии возмущений, вектор отклонений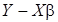 
выражается через ошибки оценивания:
,
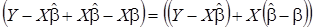и аргумент функции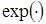 
представляет собой функцию двух слагаемых:
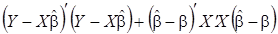, (9)
первое слагаемое включает ошибку оценки (прогноза) эндогенной переменной, второе - ошибку оценки вектора параметров. Выразим первое слагаемое через несмещенную оценку дисперсии возмущений
,
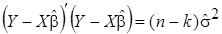и подставим оба слагаемых в формулу плотности (8):
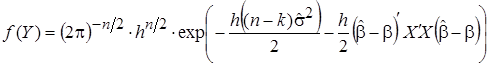. (10)
САЗ-апостериорное распределение (6) для параметров модели множественной регрессии, с учетом того что параметр точности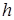 
принимает положительные значения, правила (5) и формулы (10), принимает вид многомерного гамма-нормального распределения с параметром сдвига 
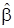, матрицей точности 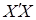и параметрам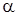и 
и :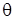
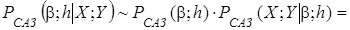
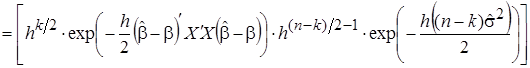, (11)
где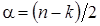 
, 
,
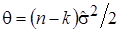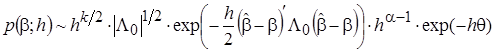. (12)
Для определения параметров байесовской регрессии аналитическим способом, необходимо вычислить параметры сопряженного с наблюдаемой генеральной совокупностью априорного распределения. Обычно для этой цели применяется метод моментов, использующий оценки числовых характеристик, полученные по выборочным данным в рамках ММП-оценивания.
В качестве примера рассмотрим оценку параметров модели линейной регрессии байесовским методом по данным таблицы 1.
Таблица 1
Выборочные данные [3]
|
№ |
Y |
X |
№ |
Y |
X |
|
1 |
6,7 |
2,8 |
8 |
10,8 |
4,8 |
|
2 |
6,9 |
2,8 |
9 |
10,6 |
4,9 |
|
3 |
7,2 |
3 |
10 |
10,7 |
5,2 |
|
4 |
7,3 |
2,9 |
11 |
11,1 |
5,4 |
|
5 |
8,4 |
3,4 |
12 |
11,8 |
5,5 |
|
6 |
8,8 |
3,9 |
13 |
12,1 |
6,2 |
|
7 |
8,5 |
4 |
14 |
12,4 |
7 |
Оценим частное распределение параметра точности h в нормальной части распределения (12). Он имеет гамма-распределение с параметрам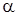и и 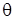. Используя значения числовых характеристик и метод моментов, получим:
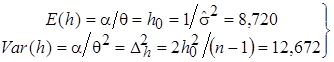, (13)
, 
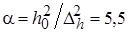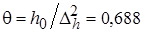. (14)
Оценим частное распределение параметра 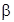, имеющего обобщённое (
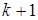)-мерное распределение Стьюдента с 
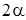числом степеней свободы, параметром сдвига 
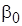и матрицей точности 
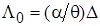. Числовые характеристики параметра 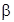определяются по формулам:
, 
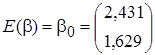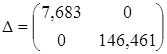
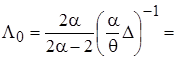
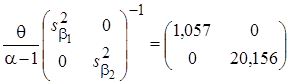, (15)
где диагональные элементы матрицы точности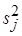 
представляют собой априорные (заданные) значения дисперсий элементов вектора параметров 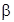. Далее вычисляются точечные оценки параметров апостериорного распределения (12) и параметры частного апостериорного гамма-распределения параметра точности:
,
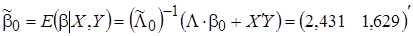где
,
,
.
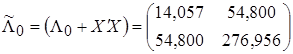
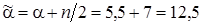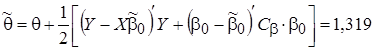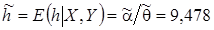Интервальные оценки вычисляются через элементы матрицы точности:
,
,
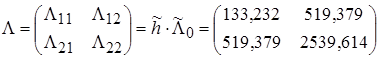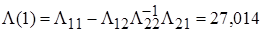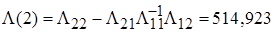, (16)
по формулам:
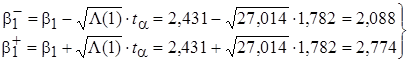, (17)
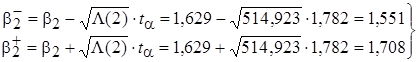, (18)
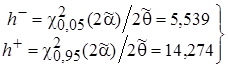. (19)
При практической реализации алгоритма байесовского оценивания, в пакетах прикладных программ, выполняется многократное генерирование случайных величин с заданным распределением. Эффективными средствами генерации таких выборок являются итерационные методы Монте-Карло, использующие цепи Маркова MCMC (Monte Carlo Markov chain) [4]. Для генерации выборки, как правило, используются методы Гиббса (Gibbs sampler) и Метрополиса-Гастингса (Metropolis-Hastings sampler). В генераторе Гиббса вначале инициализируется начальный вектор параметров, например для рассматриваемой регрессионной модели с двумя параметрами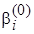 
, 
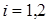. Затем генерируются последовательности случайных величин из условных апостериорных распределений [5; 6]:
, 
,
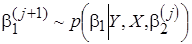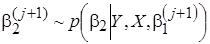где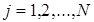 
- номер итерации. В итерационном алгоритме Метрополиса-Гастингса используются два распределения: априорное (
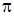) - вероятности перехода в цепи Маркова и целевое апостериорное 
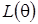, учитывающее априорное и функцию правдоподобия. Для начального вектора параметров 
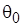вычисляются исходные значения цепи 
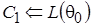. Далее с учетом распределения 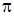текущий вектор преобразуется в 
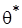и вычисляется отношение апостериорных плотностей 
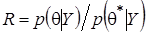, определяющее параметры следующего звена цепи 
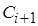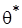- (итерация принимается), либо остаются значения цепи предыдущего шага. Результат итерационного процесса - точечная аппроксимация распределения 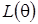[4]. Число итераций назначается достаточно большим, 
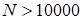, для того чтобы марковская цепь успела сойтись к своему стационарному распределению.
Точечную и интервальную оценку параметров регрессионной модели байесовским методом в программной среде R можно выполнить при помощи функции MCMCregress пакета MCMCpack
MCMCregress(formula, data, b0=b0,B0=B0)
с основными параметрами: formula – спецификация регрессионной модели; data - данные в форме data.frame; b0 - априорное среднее значение вектора параметров; B0 - априорное значение автоковариационной матрицы оценок параметров. В таблице 2 приведен фрагмент протокола результатов оценивания регрессионной модели байесовским методом по данным таблицы 1.
Таблица 2
Результаты оценивания
|
Результаты MCMC-оценивания |
Результаты МНК-оценивания |
|
1. Empirical mean and standard deviation for each variable, plus standard error of the mean: Mean SD Naive SE Time-series SE (Int) 2.797 0.366 0.004 0.0037 X 1.526 0.081 0.001 0.0008 sigma2 0.252 0.118 0.001 0.0013
2. Quantiles for each variable: 2.5% 25% 50% 75% 97.5% (Int) 2.069 2.560 2.807 3.040 3.500 X 1.371 1.472 1.524 1.578 1.688 sigma2 0.112 0.172 0.224 0.299 0.561 |
Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.43118 0.36076 6.739 3.20e-05 X 1.62947 0.08263 19.720 6.22e-10 Residual standard error: 0.3387 on 11 degrees of freedom Multiple R-squared: 0.9725, Adjusted R-squared: 0.97 F-statistic: 388.9 on 1 and 11 DF, p-value: 6.217e-10
confint(fm, level=0.90) 5 % 95 % (Intercept) 1.783295 3.079061 X 1.481071 1.777860 |
Важным этапом оценивания в рамках МСМС, для получения корректных оценок математических ожиданий на основе сгенерированных инвариантных распределений, является проверка выполнения двух ограничений: эргодичности и сходимости Марковской цепи. Для выполнения тестирования данных предпосылок в программной среде R имеется целый арсенал тестов в пакете coda: geweke.diag ( ) (Geweke), gelman.diag( ) (Gelman and Rubin), heidel.diag( ) (Heidelberger and Welch), raftery.diag( ) (Raftery and Lewis). Ниже приводится протокол результатов диагностики при помощи теста raftery.diag():
raftery.diag(m)
Quantile (q) = 0.025
Accuracy (r) = +/- 0.005
Probability (s) = 0.95
Burn-in Total Lower bound Dependence
(M) (N) (Nmin) factor (I)
(Intercept) 3 4095 3746 1.090
X 2 3771 3746 1.010
sigma2 2 3741 3746 0.999
В последнем столбце протокола - оценка «коэффициента зависимости» степени, до которой автокорреляция увеличивает требуемый размер выборки (bound Dependence factor (I)). Значения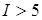 
указывают на сильную автокорреляцию, которая может быть связана с плохим выбором начального значения или высокими апостериорными корреляциями. В рассматриваемом примере этот показатель меньше 5 для всех параметров модели, следовательно, проблем со сходимостью нет.
Заключение. Результат оценивания модели множественной регрессии (7), по данным таблицы 1, в рамках аналитического байесовского подхода, алгоритм которого включает: проверку условия существования сопряженного семейства априорных распределений; определение общего вида семейства априорных распределений, сопряженных с функцией правдоподобия, и подбор значений их параметров; трансформацию значений параметров при переходе от априорного сопряженного распределения к апостериорному - показывает значительное повышение точности интервального оценивания по сравнению с классическим ММП-оцениванием и оценками в рамках метода MCMC.
Данный факт особенно важен для повышения мотивации бакалавров экономических направлений вузов к изучению байесовского подхода в статистике и эконометрике и к его использованию при изучении специальных дисциплин, ориентированных на будущую профессию. Задача преподавателей - разработать методику обучения байесовского подхода в эконометрике с использованием современных эконометрических пакетов в форме специально адаптированных программных продуктов. В данной статье для реализации байесовского подхода в эконометрике предлагается использовать программную среду R, которая пользуется широкой поддержкой научного сообщества, сообщества разработчиков и пользователей и применяется при решении базовых задач высшей математики студентами общеэкономических специальностей Финансового университета. R позволяет создавать программы с высокой степенью интерактивности обучаемого, что очень важно для процесса обучения [7].
Библиографическая ссылка
Бабешко Л.О. БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИКЕ И ЕГО РЕАЛИЗАЦИЯ В ПРОГРАММНОЙ СРЕДЕ R // Современные проблемы науки и образования. 2019. № 3. ;URL: https://science-education.ru/ru/article/view?id=28938 (дата обращения: 04.04.2025).