Неотъемлемой частью физического образования является формирование умений решать задачи разного уровня сложности, в том числе и экспериментальные задачи. Особенность экспериментальных задач заключается в том, что абстрактные научные знания по физике в представлении учащихся приобретают реальный смысл, приближая их к изучению окружающего мира. Экспериментальные задачи по физике активизируют внимание обучающихся на уроках, повышают их интерес к предмету, у учащихся появляется желание самим добывать знания, также формируются навыки самостоятельной работы учащихся.
Решение экспериментальных задач является сложной деятельностью, которую не всегда в полной мере удается формировать у учащихся. Деятельностный подход в обучении предлагает выделять действия, которые являются общими для частных видов деятельности, их называют обобщенными приемами [1].
Цель исследования: изучить эффективность обобщенных приемов при формировании умений решать качественные экспериментальные задачи по физике.
Материал и методы исследования
Формирование обобщенного приема занимает значительно меньше времени, чем формирование умений решать конкретные экспериментальные задачи, так как спектр таких задач обширный.
Экспериментальные задачи можно классифицировать по трем категориям [2]: 1) качественные экспериментальные задачи; 2) количественные экспериментальные задачи; 3) творческие экспериментальные задачи. Качественные экспериментальные задачи поставлены на конкретной физической установке и не требуют для решения количественных данных и математических расчетов. Количественные задачи требуют решения путем математического расчета данных, полученных экспериментально. Творческие экспериментальные задачи представляют собой модель научной задачи, в которой дается конечная цель, но какие-либо четкие указания, инструкции к достижению цели отсутствуют. Каждая из категорий делится на 2 типа. Качественные задачи можно разделить на 2 типа: тип 1 – экспериментальные задачи на воспроизведение явления в конкретной ситуации, тип 2 – экспериментальные задачи на предсказание результата эксперимента. Типы количественных задач: тип 1 – экспериментальные задачи-упражнения, тип 2 – собственно экспериментальные задачи. Тип 1 творческих задач – экспериментальные задачи на исследование конкретного физического процесса, требующего от ученика самостоятельного поиска метода решения, составления плана исследования с использованием тех приборов и оборудования, которые заранее ему были выданы. Тип 2 творческих задач – задачи-исследования, требующие от ученика самостоятельного поиска пути решения, составления плана исследования, а также выбора приборов и оборудования для достижения цели.
Для решения экспериментальных задач ученик должен применить не только практические, но и методологические умения, к которым относится усвоение теоретических знаний о методах научного познания. Теоретические методологические умения лучше начинать формировать в процессе решения качественной экспериментальной задачи 1-го типа. Целью задачи 1-го типа является воспроизведение явления в конкретной ситуации, для чего сначала нужно выделить признаки физического явления, затем подобрать приборы и оборудование, составить программу проведения эксперимента и воспроизвести явление. Исходя из этого приведем пример применения обобщенного приема по воспроизведению физических явлений в конкретной ситуации (тип 1 качественной задачи) на основании логической схемы, составленной С.В. Анофриковой и др. [1, 3].
Пример решения качественной экспериментальной задачи 1-го типа
Задача: Установить зависимость расстояния между дифракционными максимумами (минимумами) от вида монохроматической волны (используйте лазер с красными и зелеными лучами).
Шаг 1 – из условия задачи выявляем термин, обозначающий исследуемое физическое явление (Дифракция световых волн).
Шаг 2 – даем термину определение (Дифракция световых волн – явление отклонения световой волны от прямолинейного распространения при прохождении через малые отверстия или огибании волной малых препятствий, в результате которых возникает дифракционный спектр).
Шаг 3 – из определения физического явления находим его структурные элементы: материальный объект I (МО I); материальный объект II (МО II); условие взаимодействия (УВ); результат взаимодействия (МО I – световая волна; МО II – малое препятствие; взаимодействие и условие взаимодействия – огибание световой волны малого препятствия; результат – дифракционный спектр).
Шаг 4 – указываем элементы экспериментальной установки (ЭУ), с помощью которых будем воспроизводить физическое явление: объект исследования (ОИ); воздействующий объект (ВО); индикатор; управляющие элементы (УЭ), с помощью которых ОИ и ВО должны приводиться в контакт (ОИ – монохроматический параллельный пучок света; ВО – тонкая нить; индикатор – расстояние между максимумами (минимумами) дифракционного спектра; УЭ – элементы, с помощью которых лучи света попадают на тонкую нить, и происходит огибание светом препятствия).
Шаг 5 – составляем принципиальную схему ЭУ (Схема: монохроматический параллельный пучок от лазера падает на тонкую нить, огибает и падает на экран в виде дифракционных максимумов и минимумов).
Шаг 6 – подбираем приборы для ЭУ (Полупроводниковый лазер с красными лучами, тонкая нить на держателе, линейка, экран).
Шаг 7 – монтируем ЭУ (Проводим монтаж ЭУ).
Шаг 8 – воспроизводим явление (Проводим эксперимент сначала с лазером с красными лучами, а затем с зелеными лучами, измеряем расстояние между дифракционными максимумами).
Шаг 9 – формулируем результат эксперимента (При изменении источника света изменяется расстояние между дифракционными максимумами (минимумами), расстояние между максимумами спектра красного цвета больше, чем у спектра зеленого цвета).
Педагогический эксперимент проходил среди учащихся 11-го класса (24 человек) на базе МОБУ «Технический лицей Н.А. Алексеевой» г. Якутска Республики Саха (Якутия). Было проведено 10 экспериментальных уроков, тематический план которых приведен в таблице 1.
Таблица 1
Тематическое планирование
|
№ |
Тема урока |
Цель урока |
Содержание урока |
|
1 |
Вводное занятие |
Входной контроль знаний и умений решать качественные экспериментальные задачи |
Учащиеся решают ряд качественных экспериментальных задач |
|
2 |
Определение физического явления |
Формировать умения: – указать из условия задачи термин, обозначающий название физического явления; – дать определение данному термину |
Учащимся предлагается ряд задач, в которых они должны указать термин физического явления и дать его определение |
|
3 |
Структурные элементы физического явления |
Формировать умение выделять структурные элементы физического явления |
В ряде задач из определения физического явления учащиеся должны выделить его структурные элементы: МО I, МО II, УВ и результат взаимодействия |
|
4 |
Характеристики элементов экспериментальной установки |
Формировать умение устанавливать характеристики элементов экспериментальной установки |
Учащиеся в задачах указывают характеристики элементов ЭУ для воспроизведения явления |
|
5 |
Воспроизведение физических явлений |
Формировать экспериментальные умения: – составить принципиальную схему; – подобрать приборы; – смонтировать установку; – воспроизвести явление |
Учащиеся при решении ряда задач должны: – составить принципиальную схему ЭУ; – подобрать приборы для ЭУ; – смонтировать ЭУ; – воспроизвести явление |
|
6 |
Промежуточный контроль знаний и умений |
Промежуточный контроль знаний и умений по применению обобщенного приема к конкретным задачам |
Учащиеся решают ряд качественных экспериментальных задач |
|
7–9 |
Решение качественных экспериментальных задач с использованием обобщенного приема |
Закрепить умения и навыки решения качественных экспериментальных задач с использованием обобщенного приема |
Учащиеся применяют обобщенный прием к конкретным качественным экспериментальным задачам |
|
10 |
Итоговое занятие |
Выходной контроль знаний и умений решать задачи |
Учащиеся выполняют контрольную работу |
Результаты исследования и их обсуждение
Результаты педагогического эксперимента проанализировали с использованием методов математического статистического анализа.
Коэффициент полноты выполнения обобщенного приема по решению экспериментальных задач 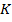 вычислили, используя методику, предложенную авторами [4]:
вычислили, используя методику, предложенную авторами [4]: 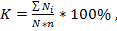 где
где 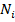 – число правильно выполненных действий -тым учащимся;
– число правильно выполненных действий -тым учащимся; 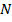 – общее число действий;
– общее число действий; 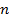 – число учащихся.
– число учащихся.
Значения коэффициентов полноты выполнения каждого действия, указанного отдельно по шагам (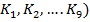 , приведены в таблице 2.
, приведены в таблице 2.
Таблица 2
Значения коэффициентов полноты выполнения действий (%)
|
|
|
|
|
|
|
|
|
|
|
|
Исходный срез |
71 |
0 |
0 |
0 |
50 |
33 |
25 |
38 |
38 |
|
Промежуточный срез |
100 |
71 |
0 |
0 |
50 |
100 |
100 |
75 |
25 |
|
Конечный срез |
100 |
100 |
88 |
79 |
100 |
100 |
100 |
100 |
100 |
Сравнение данных трех срезов показало, что в конце обучения учащиеся научились применять обобщенный прием решения к конкретным экспериментальным задачам. В начале обучения учащиеся не могли указать, какое физическое явление описано в условии задачи, затруднялись давать определение физического явления. В процессе обучения трудными оказались операции третьего действия: выделение из определения физического явления двух взаимодействующих объектов, условий их взаимодействия, результата их взаимодействия. Наиболее низкий коэффициент освоения в конце обучения имеет четвертое действие, заключающееся в определении характеристик структурных элементов экспериментальной установки.
Для первичной статистической обработки данных вычислили среднее арифметическое значение 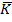 , дисперсию
, дисперсию 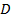 , среднее квадратичное отклонение
, среднее квадратичное отклонение 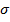 , коэффициент вариации
, коэффициент вариации 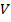 , а также ошибку средней арифметической
, а также ошибку средней арифметической 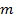 вариационных рядов, значения которых приведены в таблице 3.
вариационных рядов, значения которых приведены в таблице 3.
Таблица 3
Основные характеристики статистического распределения экспериментальных данных
|
|
|
|
|
|
|
|
Исходный срез |
28 |
63 |
7,9 |
28 |
1,62 |
|
Промежуточный срез |
58 |
66 |
8,1 |
14 |
1,66 |
|
Итоговый срез |
96 |
49 |
7,0 |
7 |
1,43 |
Из таблицы 3 видно, что коэффициент полноты выполнения обобщенного приема 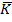 в конце обучения повысился. В итоговом срезе дисперсия
в конце обучения повысился. В итоговом срезе дисперсия 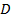 и среднее квадратичное отклонение
и среднее квадратичное отклонение 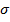 вариантов уменьшились, что показывает увеличение плотности результатов выборки. Значения коэффициентов вариации
вариантов уменьшились, что показывает увеличение плотности результатов выборки. Значения коэффициентов вариации 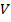 показывают однородность трех выборок, степень однородности выборок к концу обучения увеличивается. По величине ошибки средней арифметической
показывают однородность трех выборок, степень однородности выборок к концу обучения увеличивается. По величине ошибки средней арифметической 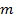 можно судить о «колеблемости» средней величины коэффициента
можно судить о «колеблемости» средней величины коэффициента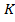 . Увеличение плотности и однородности выборок к концу обучения свидетельствует о достижении сравнительно одинаково успешных результатов обучения.
. Увеличение плотности и однородности выборок к концу обучения свидетельствует о достижении сравнительно одинаково успешных результатов обучения.
Затем проверили нормальность распределения вариационных рядов, используя гипотезу М.А. Плохинского [5]. Гипотеза гласит: «Если показатели асимметрии 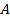 и эксцесса
и эксцесса 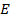 превышают свои ошибки репрезентативности
превышают свои ошибки репрезентативности 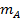 и
и 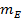 в 3 и более раза, то можно говорить о достоверном отличии эмпирических распределений от нормального распределения». Рассчитали показатели асимметрии
в 3 и более раза, то можно говорить о достоверном отличии эмпирических распределений от нормального распределения». Рассчитали показатели асимметрии 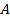 и эксцесса
и эксцесса 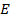 по формулам:
по формулам:
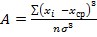 и E
и E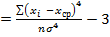
и сопоставили с их ошибками репрезентативности 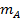 и
и 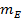 :
:
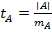 , где
, где 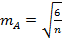 ;
; 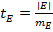 , где
, где 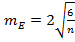
Результаты сопоставлений приведены в таблице 4.
Таблица 4
Проверка нормальности эмпирического распределения 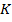
|
|
|
|
|
|
|
|
|
Исходный срез |
1,14 |
–0,17 |
0,5 |
1 |
2,3 |
0,17 |
|
Промежуточный срез |
1,05 |
1,67 |
0,5 |
1 |
2,1 |
1,67 |
|
Итоговый срез |
1,41 |
1,15 |
0,5 |
1 |
2,8 |
1,15 |
Результаты расчета, приведенные в таблице 4, доказали, что эмпирическое распределение вариационного ряда близко к нормальному распределению. В связи с этим при статистической обработке данных применяем параметрические методы.
Выдвигаем статистическую нулевую гипотезу 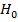 – обучение обобщенному приему решения задач в группе испытуемых в середине обучения и после обучения не дало существенных положительных изменений. Выдвигаем альтернативную гипотезу
– обучение обобщенному приему решения задач в группе испытуемых в середине обучения и после обучения не дало существенных положительных изменений. Выдвигаем альтернативную гипотезу 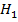 – обучение обобщенному приему решения задач в середине обучения и после обучения дало существенные положительные результаты. Мы исследовали одну и ту же группу трижды (до, в середине и после педагогического воздействия), поэтому выборки зависимы между собой. Так как ряды двух выбранных выборок однородны и подчинены нормальному закону, для выявления различий между двумя выборками использовали параметрический параметр -критерий Стьюдента [5]:
– обучение обобщенному приему решения задач в середине обучения и после обучения дало существенные положительные результаты. Мы исследовали одну и ту же группу трижды (до, в середине и после педагогического воздействия), поэтому выборки зависимы между собой. Так как ряды двух выбранных выборок однородны и подчинены нормальному закону, для выявления различий между двумя выборками использовали параметрический параметр -критерий Стьюдента [5]:
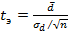 ,
,
где 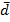 – среднее значение разности всех пар показателей;
– среднее значение разности всех пар показателей; 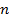 – число пар наблюдений. Стандартное отклонение среднего значения разности
– число пар наблюдений. Стандартное отклонение среднего значения разности 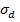 рассчитали по формуле:
рассчитали по формуле:
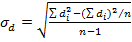 .
.
Из таблицы 5 видно, что эмпирические значения критерия 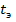 существенно превышают табличный критерий
существенно превышают табличный критерий 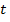 при всех уровнях значимости.
при всех уровнях значимости.
Таблица 5
Сравнение экспериментальных 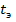 и табличного
и табличного 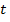 критериев Стьюдента
критериев Стьюдента
|
|
|
|
|
|
23,7 |
28,5 |
89,9 |
3,76 |
Заключение
Результаты проведенного эксперимента доказывают эффективность разработанной методики обучения учащихся решению экспериментальных задач по физике с использованием обобщенных приемов. Владение обобщенным приемом помогает учащимся грамотно, осознанно выполнять конкретные действия при решении экспериментальных задач. Достоверность результатов педагогического эксперимента доказана методами математической статистики.
Библиографическая ссылка
Тарасова Н.М., Петрова Р.И. МЕТОДИКА ОБУЧЕНИЯ УЧАЩИХСЯ РЕШЕНИЮ ЭКСПЕРИМЕНТАЛЬНЫХ ЗАДАЧ ПО ФИЗИКЕ // Современные проблемы науки и образования. 2019. № 2. ;URL: https://science-education.ru/ru/article/view?id=28754 (дата обращения: 06.03.2026).




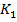
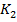
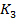
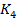
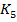
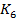
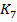
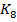
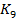
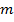
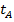
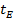
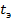 (исходный срез – промежуточный срез)
(исходный срез – промежуточный срез)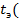 промежуточный срез – конечный срез)
промежуточный срез – конечный срез)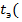 исходный срез – конечный срез)
исходный срез – конечный срез)