Судебно-медицинская диагностика давности наступления смерти (ДНС) человека в последние годы развития медицинской науки основывается на количественных характеристиках процессов, регистрируемых объективно инструментальными методами. Одним из таких посмертных процессов, наиболее часто измеряемым с целью диагностики ДНС, является охлаждение мертвого тела [1].
Регистрация скорости охлаждения трупа производится современными высокоточными термоизмерителями [2], в специально изученных и официально рекомендованных диагностических зонах (головной мозг, печень, прямая кишка) [3], в соответствии с требованиями руководящих нормативных документов [4]. В действующих приказах и правилах, регламентирующих процедуру осмотра места происшествия и трупа на месте его обнаружения, в частности в «Правилах работы врача-специалиста в области судебной медицины при наружном осмотре трупа на месте его обнаружения (происшествия)», указывается, что регистрация температуры тела производится не менее чем двукратно, через определенный интервал времени, с обязательным учетом температуры окружающей среды.
Двукратное измерение температуры позволяет эксперту установить скорость охлаждения мертвого тела, применив для определения ДНС расчетный способ [4]. Как указывалось в литературе [5], если до момента осмотра мертвого тела не изменялись условия его теплообмена с окружающей средой, например изменением положения трупа, его частей тела по отношению друг к другу и т.д., точность расчета ДНС может быть достаточно высокой.
Измерение температуры трупа три или четыре раза позволяет, помимо скорости охлаждения, определить некоторые другие особенности регистрируемого процесса по кривизне отслеживаемого температурного тренда, рассчитав, например, индивидуальную продолжительность первоначального температурного плато исследуемой диагностической зоны [6], еще больше уменьшив величину погрешности определения ДНС [7].
Для финального расчета, как правило, используются математические методики, основанные на описании температурного тренда экспоненциальными уравнениями [8]. Проверки адекватности этих моделей показали, что именно они являются приоритетными для практического применения, как обладающие наивысшей точностью описания процесса охлаждения трупа в условиях неизменных внешних температурных условий [9]. Одной из самых часто используемых математических моделей является аналитическое решение двухэкспоненциальной модели C. Hennsge, предложенное В.А. Куликовым [10]. Формула В.А. Куликова характеризуется высокой точностью и оперативностью исчисления, что позволяет применять ее непосредственно в условиях осмотра места происшествия и трупа на месте его обнаружения. Удобство использования указанной формулы привело к тому, что именно это математическое выражение принято за основу современной методики термометрического установления ДНС, официально разрешенной к практическому применению в судебно-медицинских экспертизах [11].
При всех преимуществах указанного выражения оно имеет и определенное ограничение: использование только в условиях относительно постоянных внешних температур. Говоря о «постоянстве внешних температур» на месте реального происшествия, любой специалист в области судебно-медицинской экспертизы понимает, что оно относительное, т.к. некоторые колебания температуры окружающего труп воздуха, безусловно, имеют место быть во всем диапазоне времени пребывания трупа на исследуемом участке местности. Частично эти колебания могут быть учтены при выполнении мероприятий по «оптимизации начальных условий теплового моделирования» [12; 13], однако в тех случаях, когда колебания температуры окружающей среды были существенными, применение оптимизационных алгоритмов может оказаться бесперспективным. Это может привести к ошибкам определения ДНС, появлению у практикующего эксперта разочарованности в используемых методиках, неверия в возможность их практического использования и, как следствие, отказу от последующего их применения.
Между тем столь радикальное суждение, по нашему мнению, не является адекватным способом решения проблемы.
В судебно-медицинской науке описаны способы адаптации математических моделей, описывающих процесс постмортального охлаждения, для их работы в условиях нестабильных внешних температур [14]. Так, в частности, Е.Ф. Швед, модернизируя хорошо известное математическое выражение Marshall и Hoare, предлагает проводить моделирование охлаждения трупа дискретно, разбив весь описываемый период на подпериоды различной продолжительности таким образом, чтобы внутри каждого из подпериодов температуру внешней среды можно было бы принять в качестве константы [14].
Аналогичный подход было решено применить и авторами настоящей статьи, что позволило сформулировать цель исследования: адаптировать математическую модель, предложенную В.А. Куликовым для описания охлаждения трупа, с возможностью работы адаптированного варианта в условиях внешних нестабильных температур, с ее проверкой на материале реальных объектов судебно-медицинской экспертизы.
Материал и методы исследования
Исследование проведено на базе Бюджетного учреждения здравоохранения Удмуртской Республики «Бюро судебно-медицинской экспертизы Министерства здравоохранения Удмуртской Республики» (БУЗ УР «БСМЭ МЗ УР») в период 2008-2018 гг. Термометрическому изучению подвергнута динамика охлаждения 64 трупов лиц обоего пола, различного возраста. Термометрия проводилась в сроки от 4 до 18 часов посмертного периода непосредственно на месте первоначального обнаружения трупа.
Измерение температуры проводили в глубине печени и в головном мозге, температуры воздуха – на уровне исследуемой диагностической зоны, с помощью высокоточного электронного термометра с игольчатым датчиком оригинальной конструкции с разрешающей способностью 0,004 °С (рис. 1). Примененный термоизмеритель метрически стандартизован и имеет соответствующее свидетельство об утверждении его в качестве средства медицинской диагностики (RU.C.39.001.A № 52334).

Рис. 1. Электронный микропроцессорный термоизмеритель
Термометрия диагностических зон выполнялась в соответствии с требованиями действующей медицинской технологии, зарегистрированной и разрешенной к применению Министерством здравоохранения и социального развития Российской Федерации [11].
Замеры производили не менее чем 4-кратно (а в некоторых случаях значительно большее число раз), с интервалом в 10-15 минут, для создания «выборки процесса», на основании которой возможно достоверное суждение об общих тенденциях охлаждения тела.
В каждом случае осуществлен перерасчет температуры тела для описания ее безразмерной величиной [14; 15].
Экспериментальное исследование по изучению влияния изменений внешних температурных условий на динамику охлаждения мертвого тела проведено в условиях секционного зала БУЗ УР «БСМЭ МЗ УР» на трупах, давность смерти которых не превышала 1,5-2,0 часа. Трупы помещались на каталку, подключались к термоизмерителю, выдерживались в течение 4 часов, для стабилизации их температурного режима, после чего перемещались в иные температурные условия. После стабилизации процесса охлаждения трупа в новых температурных условиях мертвое тело перемещалось обратно. Таким образом, было изучено 16 трупов с точно известной давностью смерти.
Все результаты измерения температур трупа вносились в базу данных, сформированную в программе Microsoft Excel, и обрабатывались традиционными методами количественной статистики.
Результаты исследований и их обсуждение
Произведена модификация математической модели В.А. Куликова, заключающаяся во введении дополнительного уравнения, описывающего охлаждение поверхностных отделов тела (ТП), и установление математической связи между ТП и температурой диагностической зоны (ТТ), путем введения ТП в основное выражение, моделирующее изменение ТТ в продолжении постмортального периода.
Итоговое выражение, условно обозначенное как «адаптивный вариант модели В.А. Куликова», представляется в следующем виде:
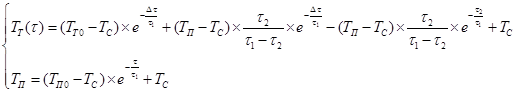 (1)
(1)
где ТТ0 – внутренняя (прижизненная) температура тела, °С;
ТП – температура внешнего слоя (поверхности тела), °С;
ТП0 – прижизненная температура внешнего слоя, °С;
ТС – температура среды, °С;
t – время (ДНС), час;
Δt - продолжительность интервала моделирования, час;
t1 – постоянная времени экспоненты регулярной стадии охлаждения;
t2 – постоянная времени нерегулярной стадии охлаждения.
Произведя моделирование температуры трупа по выражению (1), представим полученные температурные кривые в соотношении их с реальной динамикой охлаждения мертвого тела, зарегистрированной в интервале от 4 до 18 часов посмертного периода в условиях осмотра места происшествия и трупа на месте его обнаружения. Температуру трупа регистрировали во всех трех традиционно используемых диагностических зонах (головной мозг, печень, прямая кишка).
Результаты измерений температуры в соотношении с моделируемыми температурными трендами представлены на рисунке 2.
Из представленных результатов следует, что «адаптивная» математическая модель хорошо описывает реальную динамику охлаждения мертвого тела.
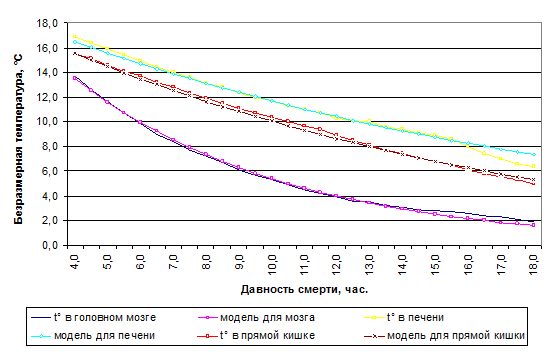
Рис. 2. Температурные тренды охлаждения стандартных диагностических зон в соотношении с результатами применения «адаптивной» математической модели
Указанный вывод подтверждается высокими значениями корреляции (таблица) между реальным диагностическим процессом и его описанием с помощью разработанной модели. Кроме того, низкие значения дисперсии также подтверждают сказанное (т.н. метод наименьших квадратов отклонений).
Характеристики соотношения адаптивной математической модели с реальной динамикой охлаждения тел
|
Краниоэнцефальная термометрия |
Термометрия печени |
Ректальная термометрия |
|
|
Корреляция |
0,999 |
0,996 |
0,999 |
|
Дисперсия |
0,016 |
0,078 |
0,014 |
Моделируя нестабильность внешних температурных условий (см. Материал и методы исследования), мы намеренно создавали резкое, скачкообразное изменение внешней температуры, т.к. труп, как и любой другой реальный объект физического мира, имеет температурную инерцию, существование которой может не проявиться при плавном изменении температуры окружающей среды, но обязательно будет выявлено при резком ее изменении.
Поведение математической модели при скачкообразном изменении температуры окружающей среды продемонстрировано на рисунке 3.

Рис. 3. Поведение адаптивной математической модели при скачкообразных изменениях температуры окружающей среды
Как следует из представленного рисунка (рис. 3), при резком, скачкообразном, изменении температуры окружающей среды максимальная ошибка моделирования температуры трупа, отмеченная к концу периода наблюдения (18 часов), составила 1,094 °С. Значения дисперсии и коэффициента корреляции между реальными и расчетными значениями температуры трупа составили 0,111 и 0,999 соответственно. Получение таких результатов однозначно свидетельствует о высокой степени соответствия моделируемой температуры трупа ее реальным значениям.
Практическое применение разработанного «адаптивного варианта математической модели В.А. Куликова» было реализовано нами с помощью средств Microsoft Excel, созданием листа расчета (рис. 4), в который предварительно введены разработанные формульные выражения, и задачей судебно-медицинского эксперта является только указание четырех значений температуры трупа, измеренной им на месте происшествия в соответствующей диагностической зоне. Учет нестабильности внешних температурных условий реализуется путем указания периода времени, в течение которого наблюдалась указанная нестабильность, и значений температур, соответствующих минимальным и максимальным ее значениям в течение наблюдения.
Моделирование динамики охлаждения трупа сопровождается визуализацией процесса на графике, отображаемом на листе расчета (рис. 4).
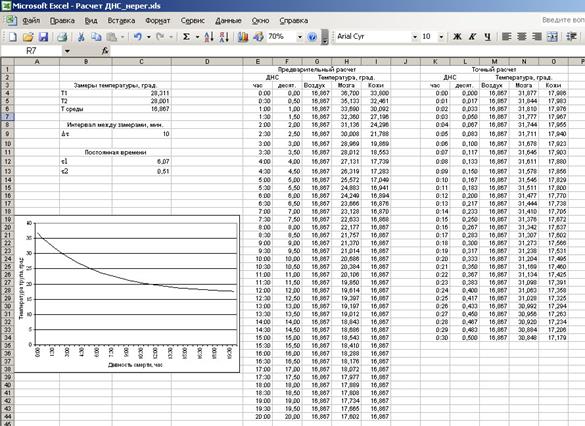
Рис. 4. Лист Microsoft Excel, реализующий пошаговый алгоритм расчета ДНС («адаптивная модель»)
Значение ДНС шага, на котором произошло совпадение моделируемой температуры трупа и реальной температуры, зафиксированной в ходе осмотра трупа на месте его обнаружения, принимается в качестве искомой ДНС.
Выводы
1. Разработан вариант математической модели, предложенной В.А. Куликовым для описания динамики температуры трупа в раннем постмортальном периоде, позволяющий применять его в условиях внешних нестабильных температур.
2. Достоинствами представленного решения является высокая точность моделирования, даже при резком, скачкообразном изменении температуры окружающего воздуха, хорошо описывающего динамику изучаемого процесса.
3. Реализация расчета ДНС с помощью стандартного программного пакета Microsoft Excel позволяет легко внедрить его в практику судебно-медицинских экспертиз.
4. Визуализация динамики постмортального охлаждения дает судебно-медицинскому эксперту, проводящему расчет ДНС представленным способом, возможность ручной коррекции значения термических постоянных выражения (1) для достижения полного совпадения моделируемого процесса охлаждения и его реальной диагностической выборки.
Библиографическая ссылка
Лахно А.В., Халиков А.А., Найденова Т.В., Бабушкина К.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОСТМОРТАЛЬНОГО ОХЛАЖДЕНИЯ ТРУПА ПРИ НЕСТАБИЛЬНЫХ ВНЕШНИХ ТЕМПЕРАТУРАХ // Современные проблемы науки и образования. 2019. № 1. ;URL: https://science-education.ru/ru/article/view?id=28498 (дата обращения: 27.12.2025).



