Динамика развития общества, растущие требования к будущим специалистам существенным образом влияют на приоритеты высшего, а потому и среднего образования. Именно развитие личностных характеристик обучаемых становится одной из генеральных линий обучения. Современный специалист должен быть готовым к постоянно меняющейся действительности, уметь ставить перед собой цели и достигать их, способным осуществлять исследовательскую, проектную и информационную деятельность, быть готовым к непрерывному образованию и самообразованию.
В настоящее врем вопрос о применении таких способов организации учебного процесса, которые позволяли бы сформировать у обучаемых хотя бы первичные навыки научно-исследовательской деятельности, отработать основные этапы творческого процесса, становится одним из главных в педагогике школы и профессионального образования. Нужны активные методы обучения, способствующие развитию самостоятельности мышления будущего специалиста [1]. Необходимость формирования у обучаемых компетенций исследования занимает далеко не последнее место и в Федеральных государственных образовательных стандартах. Ясно, что исследовательская деятельность в чистом виде недоступна ученикам по вполне объективным причинам, среди которых недостаток знаний, опыта в проектировании и разработке нового объекта исследования. В связи с этим будем использовать термин «проектно-исследовательская деятельность». Что представляет собой проектно-исследовательская деятельность? Это проектирование учеником собственного исследования: формулировка целей, задач, выбор наилучших способов, средств исследования, проектирование ожидаемых результатов и оценка соотношения их с полученными. Мы будем рассматривать проектно-исследовательскую деятельность как вид учебно-познавательной деятельности, в которой пропорции компонентов проектной и исследовательской деятельности меняются в зависимости от характеристик осуществляющего ее объекта. Так, у школьников главенствующую позицию должен занимать проектный компонент, компонент исследования будет сводиться к проведению мини-исследований, получению не известных ранее ученику знаний и выводов. Мини-исследования являются составными частями мини-проектов, рассчитанных на короткий промежуток времени, а затем и более весомых учебных проектов. У студентов акцент проектно-исследовательской деятельности постепенно должен смещаться в сторону исследовательской деятельности, да и проекты должны сводиться к созданию профессиональных объектов. Проектно-исследовательский подход переставляет акценты в деятельности учителя. Учитель уже не просто носитель и источник информации, который излагает ее, контролируя степень понимания учениками, дает оценку действий обучаемых о степени усвоения полученного материала. Проектно-исследовательский подход требует от учителя более профессиональных действий, мотивирующих ученика к самостоятельной постановке и решению учебной проблемы. При новом подходе учитель становится организатором их совместной, взаимодополняемой деятельности [2].
Материалы и методы исследования
К сожалению, устоявшееся содержание математического образования в большинстве своем не дает представлений ученикам о возможностях применения математического аппарата на практике. Уровень абстрагирования математических знаний давно оторвался от истоков математики как основного средства достижения практических целей. Но по объективным причинам школьный курс математики дает слабое представление и о методах исследования математики как науки. Это противоречие отрывает его и от практики, и от возможности проводить серьезные научные исследования; делает, казалось бы, бессмысленным для ученика содержание дисциплины, обесценивает личностную значимость для ученика, эмоционально его демотивирует.
Особые сложности из изучаемых в школе математических дисциплин вызывает геометрия. Хотя именно геометрия может подчеркнуть практическую значимость изучаемого материала, актуальность получаемых знаний. Но уровень абстрагирования геометрических знаний лишает их возможности применять геометрию для решения конкретных важных для ученика жизненных проблем, что принижает ее личностную значимость. Доказательный аппарат геометрии является весьма оторванным от действительности и поэтому сложным для понимания учеников. Хочется отметить потерю современным курсом школьной геометрии прикладного характера. Для успешного усвоения геометрических понятий необходимо обладать хорошо развитым геометрическим воображением, чтобы представить себе соответствующую пространственную картину. Никакое отвлеченное знание не может быть востребовано обучаемым, если ему не предшествует сознание, обогащенное нужными представлениями [3, 4].
Одним из способов разрешения сформулированного противоречия является применение наглядности и акцентирование на практической значимости геометрической задачи. Это должно усилить личностную значимость и эмоциональную мотивацию ученика в получении геометрических знаний.
Цель исследования: разработать методы и приемы, позволяющие осуществлять проектно-исследовательскую деятельность учащихся, основанные на прикладном характере геометрических знаний.
Преодолеть абстрактный характер геометрических знаний позволяют задачи, при решении которых используются повседневные материалы (например, нить, линейка, ножницы, картон для определения числа π, два колышка и веревка для построения эллипса, линейка без делений, циркуль), позволяющие решать задачи на построение. Геометрические задачи, решаемые с помощью подручных средств, позволяют подчеркнуть практическую значимость геометрических знаний. Мы же хотим остановиться на использовании бумажных фигур.
Одним из возможных действий с бумагой является операция ее перегибания. С помощью перегибания бумаги можно получить наглядное представление о многих фигурах на плоскости и их свойствах. Эта операция имеет ряд физиологических, психологических и эстетических преимуществ. С точки зрения физиологии тактильные ощущения при перегибании бумаги дают дополнительные сигналы мозгу, подтверждающие практический аспект геометрических преобразований. С точки зрения психологии перегибание листа бумаги порождает положительные эмоции от осознания обучающимися того, что геометрия не столь абстрактна, как казалась до сих пор. А неожиданные перевоплощения бумажного листа в различные образы вызывают эстетическое наслаждение. Достоинством указанной операции является также то, что ее можно производить, не имея инструментов, которые ученики обычно забывают принести: не требуется ни циркуля, ни линейки, ни карандаша, просто ничего, кроме кусочка бумаги, а потому такие задачи можно решать в любое свободное время.
Пластичные свойства бумаги, возможность получения при ее перегибании модели точек и прямых, основных понятий евклидовой геометрии, позволяют вести речь об особенной геометрии. В этой геометрии линия – это край листа или складка, точка – это вершина угла бумажного листа либо результат пересечения складок друг с другом или с краями листа. Ясно, что перегибание листа бумаги можно отнести к задачам на построение одной линейкой, форма и ограниченность листа бумаги придают им некоторые возможностями циркуля.
Еще в XIX веке Фребель обратил внимание на то, что некоторые факты геометрии легко продемонстрировать, а иногда и доказать с помощью складывания листа бумаги. Его идею более чем через 100 лет подхватил японский математик Хумиани Хузита, введя понятие «оригаметрия» [5, 6]. И это не случайно: именно Япония является законодательницей всех классических принципов оригами.
Результаты исследования и их обсуждение
Оригаметрия – это симбиоз двух наук: оригами и геометрии. Оригаметрия – это новая, привитая ветвь на дереве, называемом в математике конструктивной геометрией.
Задачи на перегибание листа бумаги нередко встречаются и среди олимпиадных задач. Их решение, как и решение любой задачи на построение, состоит из нескольких этапов [7]: постановка задачи; решение задачи методами оригами; математическое доказательство того, что полученная фигура удовлетворяет условию задачи.
Рассмотрим реализацию метода проектов при решении геометрических задач методом оригами. Исходя из двухкомпонентной реализации проектной деятельности выделим следующие этапы.
Этап первый (подготовительный). На этом этапе подчеркивается связь оригами с геометрией. Определяется новое направление «оригаметрия». Формулируются способы и средства решения задач, а именно основные действия с листом бумаги (аксиомы оригаметрии), методы решения простейших задач, основные возможные построения.
Этап второй (проектно-исследовательский). Одной из распространенных задач оригами является проблема деления одной или всех сторон квадрата на несколько равных частей. По замыслу руководителей проект «Геометрия квадратного листа бумаги и оригами» распадается на три мини-проекта. Обучаемые проводят мини-исследования, решая открытые задачи, придуманные специально для этих проектов. Однако к защите проекта, помимо решения задач, необходимо представить презентацию, позволяющую проследить последовательность перегибаний листа бумаги на экране.
Каждый мини-проект сопровождается листком-заданием, состоящим из двух частей. Первая часть – это Листок для первого знакомства, относящийся к первому компоненту проекта. Вторая часть – Листок-задание, содержащий открытые задачи, которые необходимо решить участникам проекта. Задачи, решаемые с помощью оригаметрии, широко представлены в [8, 9]. Задания мини-проектов рассчитаны на учеников 9–11-х классов с углубленным изучением математики.
Листок для первого знакомства. Геометрия листа бумаги произвольной формы
Задачей на построение называют задачу построения фигур с заданными свойствами с использованием указанного набора инструментов. Каждая фигура, удовлетворяющая условию задачи, называется решением задач.
Применяемым инструментом в оригаметрии является лист бумаги. Основным действием – «построением» – является его сгибание. Сформулируем серию аксиом, характеризующую свойства выбранного нами инструмента и его возможности для геометрических построений.
В частности, перегибанием листа бумаги можно реализовать следующие основные построения.
А1. Выполнить сгиб, проходящий через две данные точки.
А2. Выполнить сгиб, совмещающий две данные точки.
А3. Выполнить сгиб, совмещающий две данные параллельные прямые.
А4. Выполнить сгиб, совмещающий две данные пересекающиеся прямые.
А5. Выполнить сгиб, проходящий через данную точку и перпендикулярный данной прямой.
А6. Выполнить сгиб, помещающий каждую из двух данных точек на одну из двух данных пересекающих прямых.
Задание 1. Выясните количество сгибов, которые можно выполнить в каждом из основных построений А1 – А6.
Задание 2. Сформулируйте предложения евклидовой геометрии, являющиеся эквивалентными аксиомам А1 – А6.
Перегибанием листа бумаги можно выполнить следующие элементарные построения.
ЭI. Построение на данной прямой отрезка, равного данному.
Э2. Деление данного отрезка пополам.
Э3. Удвоение данного отрезка.
Э4. Построение серединного перпендикуляра данного отрезка.
Э5. Построение прямой, проходящей через данную точку и перпендикулярной данной прямой.
Э6. Построение прямой, проходящей через данную точку и параллельной данной прямой
Э7. Построение угла, равного данному.
Э8. Удвоение данного угла.
Э9. Деление данного угла пополам.
Задание 3. Решите элементарные задачи на построение ЭI – Э9.
Задание 4. Используя элементарные построения, решите следующие задачи.
1) Перегибая лист произвольной формы, сложите квадрат: а) с произвольной стороной, б) с данной стороной.
2) Можно ли из произвольного листа бумаги сложить прямоугольник?
3) Можно ли из произвольного листа бумаги сложить прямоугольник, стороны которого относятся, например, как 3:5? Возможно ли какое-нибудь другое соотношение сторон?
4) Какие виды треугольников можно получить, перегибая лист произвольной формы, используя 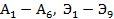 ?
?
5) Перегибая вырезанный из бумаги круг, найдите его центр.
6) Перегибая лист произвольной формы, найдите центр круга, нарисованного на этом листе без использования циркуля.
7) Даны три точки. Средствами оригами постройте центр окружности, описанной около треугольника с вершинами в этих точках.
8) Даны прямая, центр окружности и точка, лежащая на этой окружности. Средствами оригами постройте точки пересечения прямой и окружности.
Листок-задание 1. Двоичные методы деления стороны квадрата
Одной из наиболее распространенных задач оригами является проблема деления одной или всех сторон квадрата на равные части. Изучите один из способов решения этой задачи.
Двоичное деление. Неоднократно разделяя отрезок пополам, можно разделить сторону квадрата (или прямоугольника) на 2, 4, 8, ... равных частей. Эту процедуру назовем двоичным делением.
Задание 1. Дроби какого вида (назовем их двоичными) можно построить двоичным делением?
Задание 2. Найдите а)  ; б)
; б) 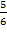 стороны квадратного листа бумаги.
стороны квадратного листа бумаги.
Задача 3. Опишите алгоритм построения двоичной дроби.
Задание 4. Представьте двоичные дроби:  ,
,  ,
,  ,
,  ,
, 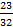 в двоичном виде.
в двоичном виде.
Задание 5. Сформулируйте алгоритм представления двоичной дроби в двоичном виде.
Задание 6. Опишите последовательность сворачиваний, определяемую двоичным представлением, для каждой цифры, начиная с правой.
Задание 7. Методом двоичного сворачивания найдите а)  , б)
, б) 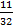 стороны квадрата.
стороны квадрата.
Задание 8. Сравнив количество сгибов, необходимых для получения двоичной дроби, определите более эффективный метод.
Задание 9. Представьте дроби  ,
,  ,
,  ,
,  ,
,  ,
,  в двоичном виде.
в двоичном виде.
Двоичные приближения. Если двоичное разложение дроби представляет собой бесконечную периодическую последовательность, то период определяет последовательность сворачиваний, которая должна быть повторена и которая последовательно приближает желаемую дробь.
Задание 10. Методом двоичного приближения найдите а)  , б)
, б)  стороны квадрата.
стороны квадрата.
Листок – задание 2. Диагональные методы деления стороны квадрата
Одной из наиболее распространенных задач оригами является проблема деления одной или всех сторон квадрата на равные части. Изучите один из способов решения этой задачи.
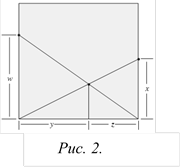
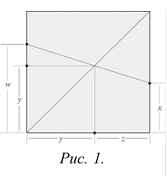
Метод диагоналей. Схема одного из самых универсальных построений оригами для получения произвольной дроби  показана на рисунке 1. Она использует две складки: одна из них – диагональ квадрата, другая соединяет две точки на противоположных сторонах.
показана на рисунке 1. Она использует две складки: одна из них – диагональ квадрата, другая соединяет две точки на противоположных сторонах.
Задание 1. Дайте математическое обоснование метода диагоналей.
Задание 2. Методом диагоналей разделите сторону квадрата на 5, 7, 9, 11 частей.
Задание 3. Можно ли методом диагоналей разделить сторону квадрата на произвольное n число частей? Если можно, сформулируйте алгоритм такого деления.
Задание 4. Решите задачи 1–3, используя «диагонали», изображенные на рисунке 2.
Алгоритм Фуджимото. Альтернативная техника для получения рациональных дробей была разработана японским математиком Шузо Фуджимото и вновь независимо открыта Бостонским топографом Джиннайном Мозели. Алгоритм Фуджимото основан на построении, показанном на рисунке 3.
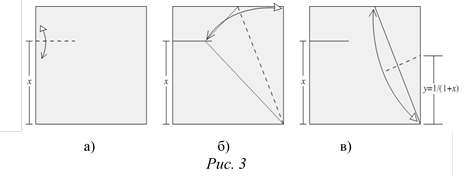
Задание 5. Дайте математическое обоснование алгоритма Фуджимото.
Задание 6. Методом Фуджимото разделите сторону квадрата на 5, 7, 9, 11 частей.
Задание 7. Можно ли методом Фуджимото разделить сторону квадрата на произвольное n число частей? Если можно, сформулируйте алгоритм такого деления
Метод Масамиши позволяет делать только два типа сгибов, создающих новые метки вдоль краев: 1) cоединять две метки на одном краю листа, 2) cоединять две метки на разных краях листа.
Способ соединения двух меток на смежных краях листа, изображенный на рисунке 4, был открыт Масамиши и носит его имя.

Задание 8. Дайте математическое обоснование алгоритма Масамиши.
Задание 9. Методом Масамиши разделите сторону квадрата на 5, 7,… частей.
Задание 10. Можно ли методом Масамиши разделить сторону квадрата на произвольное n частей? Если можно, сформулируйте алгоритм такого деления.
Листок-задание 3. Теорема Хага
Одной из наиболее распространенных задач оригами является проблема деления одной или всех сторон квадрата на равные части. Изучите один из способов решения этой задачи.
Героновыми называются прямоугольные треугольники с целочисленными сторонами. Примером таких треугольников является египетский треугольник со сторонами 3:4:5. Перегибанием квадратного листа бумаги по прямой, пересекающей его противоположные стороны, можно получить три подобных героновых треугольника.
Задание 1. Указанным выше способом постройте египетские треугольники.
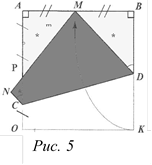
Задание 2. Повторите построения, выполненные на рисунке 5, а затем докажите следующие утверждения: треугольники APM и BMD – египетские; точка 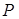 отсекает от стороны квадрата его треть, считая от вершины О.
отсекает от стороны квадрата его треть, считая от вершины О.
Доказанные в задании 2 факты впервые были обнаружены и доказаны Казуо Хага, а потому называются теоремой Хага. С помощью только одной такой складки могут быть получены все рациональные числа.
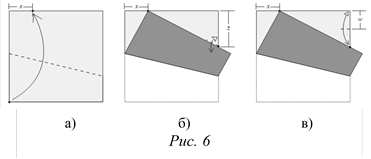
Общая схема построений Хага состоит из двух этапов и показана на рисунке 6.
Задание 3. Выразите зависимость между отрезками x, z и w, изображенными на рисунке 6, математической формулой.
Задание 4. Обоснуйте построения Казуо Хага.
Следствие из теоремы Хага, обнаруженное Хусими, позволяет отметить  стороны квадрата.
стороны квадрата.
Задание 5. Как с помощью перегибания квадратного листа получить треугольник, обладающий свойством геронового треугольника?
Задание 6. Используя построение Хага, разделите сторону квадрата на 5, 7, 9, 11 частей.
Задание 7. Можно ли, используя построение Хага, разделить сторону квадрата на произвольное n число частей? Если можно, сформулируйте алгоритм такого деления.
Заключение
Представленные мини-проекты позволяют организовать проектно-исследовательскую деятельность учащихся при подготовке к различным олимпиадам, при осуществлении индивидуальной исследовательской работы с учениками в 9–11-х классах. Использование представленные мини-проектов дает дополнительные возможности сформирования у обучаемых исследовательских компетенций. На основе разработанных материалов была организована проектная деятельность одаренных и перспективных детей Уральского федерального округа в рамках профильной смены «Эрудит» на базе федеральной экспериментальной площадки «Абзаково» [10]. Несмотря на все сложности, математические дисциплины, в частности геометрия, предоставляют нам достаточно широкие возможности для осуществления проектно-исследовательской деятельности учеников. Они могут вносить немалую лепту в личностную значимость образования учащегося, формируя положительный эмоциональный фон процесса обучения.
Библиографическая ссылка
Великих А.С., Смирнова Л.В., Торшина О.А. ОРГАНИЗАЦИЯ ПРОЕКТНО-ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ ПРИ РЕШЕНИИ НЕКОТОРЫХ ВИДОВ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ ПЕРЕГИБАНИЕМ ЛИСТА БУМАГИ // Современные проблемы науки и образования. 2018. № 6. ;URL: https://science-education.ru/ru/article/view?id=28295 (дата обращения: 16.02.2026).



