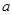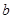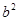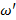На современном этапе развития системы образования к качеству подготовки учителей математики предъявляются новые требования, суть которых в формировании общекультурных, общепрофессиональных, профессиональных компетенций в соответствии с ФГОС ВО, необходимых для подготовки выпускника к педагогической, проектной и научно-исследовательской деятельности; формировании высоконравственных качеств личности, способной к творческой деятельности и саморазвитию.
Анализируя исследования по проектной деятельности, авторы отметили, что вопросы подготовки обучаемых в педагогических вузах к проектной деятельности довольно подробно описаны в работах Н.В. Кузьминой, В.А. Сластенина, А.И. Щербакова, И.С. Якиманской и других исследователей [1].
В работе И.В. Николаюк проектная деятельность рассмотрена как инструмент адаптации студентов младших курсов к учебной деятельности [2]. Комплексный характер проектной деятельности учащихся подробно описан в работе Т.П. Камыниной. Автор перечисляет основные этапы осуществления проектной деятельности: формулировка проблемы, постановка целей, прогнозирование результата, поиск путей и инструментов его достижения, а также самооценка и корректировка своей деятельности [3].
Проектная деятельность является одним из современных педагогических средств и методов, позволяющих учитывать актуальные требования общества при обучении математике. Кроме того, проектная деятельность включается в будущую профессиональную деятельность студента-бакалавра педагогического образования, т. к. современный учитель должен владеть методом проектов, уметь эффективно организовывать проектную деятельность с учащимися и на уроках, и во внеурочной деятельности. В требованиях ФГОС СОО в части метапредметных результатов освоения основной образовательной программы отмечается: «владение навыками познавательной, учебно-исследовательской и проектной деятельности, способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания».
В последнее время особое внимание в учреждениях общего и высшего образования уделяется организации проектной деятельности с учащимися при изучении профильных математических дисциплин на примере выполнения учебных проектов.
Использование учебных проектов позволяет решать сразу несколько образовательных задач при профильной подготовке будущих учителей, в том числе и учителей математики. Это и повышение уровня познавательного интереса и мотивации к изучению предмета, и организация самостоятельной работы по предмету, и вовлечение студентов в научно-исследовательскую деятельность, а также формирование профессиональных компетенций будущего учителя [4].
В большинстве работ, посвященных обучению проектной деятельности в вузе при изучении профильных математических дисциплин, рассмотрены учебные проекты при изучении дисциплин «Математический анализ» [4-6] и «Геометрия» [4; 7]. В этих дисциплинах ярко выражен прикладной характер знаний. В то время как организации по формированию проектных умений в рамках изучения дисциплины «Алгебра» не уделено должного внимания. Данная работа призвана восполнить этот пробел.
Цель данного исследования – выявление содержательных и организационных условий и требований к реализации учебных проектов по дисциплине «Алгебра», которые позволяют формировать основные общекультурные и профессиональные компетенции специалиста.
Материалы и методы исследования
В педагогическом университете формирование проектных умений начинается в рамках профильных математических дисциплин уже на младших курсах. Студентам предлагается знакомство с материалом, выходящим за рамки учебного предмета. Выполняется подготовка докладов и мини-проектов в процессе изучения этих дисциплин.
После завершения изучения базовых дисциплин, таких как алгебра, геометрия, математический анализ, в 6 семестре студентами выполняется курсовая работа - проект, требующий применения полученных теоретических знаний и практических навыков. Здесь важно составить план работы над курсовым проектом и контролировать его выполнение, не допускать поспешных выводов, небрежных, незавершенных деталей. Оставляя студенту самостоятельность в выборе темы, осуществлении проекта или исследования, подготовке доклада, стоит помнить о рамках учебного процесса, ограничении по времени выполнения работы.
Учебные проекты в зависимости от предметной области используемых математических знаний, как отмечено в [8], могут носить дисциплинарный, междисциплинарный и наддисциплинарный характер. Для того чтобы проектная деятельность учащихся была наиболее успешной, необходимо наличие площадки для поиска и постановки проектных задач (и такой площадкой может стать научно-исследовательская деятельность преподавателей), а также интеграция проектной деятельности студентов и преподавателей, взаимная оценка результатов такой работы.
Для формирования профессиональной компетентности будущего учителя математики, по мнению Т.Н. Грань [9], целесообразно выполнение учебно-методических проектов, имеющих исследовательский, творческий характер и обеспечивающих самостоятельный характер учебно-профессиональной деятельности студентов. По нашему мнению, не менее важны и проекты по профильным математическим дисциплинам, имеющие исследовательский характер. Тематика проектов должна быть такова, чтобы результаты деятельности учащихся имели определенную значимость в практической или теоретической области математики. Наибольшее значение для обучения имеют проекты, при выполнении которых применяются интегрированные знания из разных разделов математики, психологии, педагогики, методики обучения и др.
Эффективная организация учебной проектной деятельности бакалавров во многом связана с установлением межпредметных связей, с использованием практической направленности содержания этих дисциплин [5]. Учебные проекты по профильным математическим дисциплинам должны соответствовать уровню знаний студентов, обладать признаками новизны при постановке задачи или при ее решении.
Журавлева Н.А. выделяет основные дидактические условия для формирования проектных навыков учащихся в процессе обучения математическому анализу [6]:
1) процесс обучения не должен быть полностью построен на проектном методе. Во время аудиторной работы проводится начальный и заключительный этапы. Вся оставшаяся работа учащихся выполняется во внеаудиторное время;
2) проект возможно осуществлять как индивидуально, так и в группе. При первом знакомстве студентов с проектами лучше организовать групповую деятельность, так как в группе возможно проведение исследований на более высоком уровне. В определенный момент времени учащийся может работать лишь над одним проектом, будь то индивидуальный или групповой.
Учебные проекты нацелены на формирование таких проектных умений, как:
- конструктивные (выбор содержания проекта, формулирование учебных проблем, конструирование этапов проекта);
- проектировочные (проектирование направления исследования и практическая значимость проекта);
- организаторские (организация групповой, парной или индивидуальной работы, оценивание результатов деятельности, организация обработки эмпирических данных графически и математически);
- коммуникативные (обсуждение полученных результатов);
- диагностические (оценка промежуточных и конечных результатов и их защита) [10].
Методические подходы, предлагаемые авторами данной статьи, а также условия и требования применялись при осуществлении учебного проекта студентами 3 курса физико-математического факультета направления «Педагогическое образование» по профильной дисциплине «Алгебра». Учащимся установлен срок один семестр для выполнения и защиты проекта.
Результаты исследования и их обсуждение
Рассмотрим организацию проектной деятельности студентов при выполнении проекта «Представления групп малого порядка на примере групп Фробениуса». Представим деятельность студентов и результаты на каждом этапе выполнения проекта.
На первом этапе преподаватель знакомит студентов с актуальными проблемами теории групп и намечает пути их решения. Здесь происходит актуализация знаний студентов, полученных ранее при изучении дисциплины «Алгебра», взаимосвязь теории групп с линейной алгеброй, теорией чисел, физикой. В качестве формы взаимодействия преподавателя и студентов был выбран семинар, проходивший еженедельно. Также был составлен график индивидуальных консультаций.
В современной теории конечных групп широко и результативно используются методы теории представлений. В теории представлений рассматриваются конкретные реализации систем абстрактной алгебры. Эта теория берет свое начало в изучении групп подстановок и матричных алгебр. В полной и удобной для применений форме теория представлений групп была развита Фробениусом в последние два десятилетия XIX века. Благодаря исследованиям Фробениуса и Бернсайда представления групп играют важную роль в теории абстрактных конечных групп. Теория представлений связана с научной деятельностью преподавателей выпускающей кафедры [11-13] и поэтому стала площадкой для реализации данного учебного проекта.
На втором этапе студенты получили задание изучить теоретический материал теории представлений конечных групп и выполнить сравнение в построении теории у Белоногова В.А. [14] и Кострикина А.И. [15]. В ходе изучения теории представлений использовались знания разных разделов алгебры (таких, например, как линейная алгебра, теория групп). Отметим, что некоторые важные для теории представлений теоремы (например, теорема Машке) не входят в программу дисциплины «Алгебра» и требуют от студентов самостоятельного осмысления их доказательств. Это было сделано в ходе обсуждений на семинаре и индивидуальных консультациях. На этом этапе происходит формирование конструктивных и проектных умений у студентов, таких как формулировка учебных проблем, целей и задач проекта; проектирование направления исследования.
На третьем этапе было предложено рассмотреть основные положения теории представлений (характеры и соотношения ортогональности). Студенты самостоятельно изучали примеры линейных представлений из [14; 15] для групп перестановок, циклических, диэдральных групп и методы построения таблиц характеров таких групп [11-13]. Для построения таблиц характеров использовались теоретические сведения о характерах матричных представлений и соотношения ортогональности, правила построения классов сопряженных элементов. Кроме того, для групп, задаваемых определяющими соотношениями, построения выполнялись с использованием компьютерной программы GAP (Groups, Algorithms and Programming), системы компьютерной алгебры, изначально созданной как инструмент для вычислений в теории групп и впоследствии распространившейся на смежные разделы алгебры. Здесь от студентов потребовались навыки программирования и восприятия информации на иностранном языке. На этом этапе формируются коммуникативные и организаторские умения, такие как разделение обязанностей в группе исследователей, обсуждения полученных данных и результатов. Ярко выступает связь современной алгебры и программирования, необходимость освоения знаний по профессиональным дисциплинам на иностранном языке. Это подчеркивает междисциплинарный характер проекта.
На третьем этапе требовалось описать представления и построить таблицу характеров для группы Фробениуса метациклического типа. Эта задача потребовала поиска методов построения представлений, и таким методом был выбран метод индуцирования, описанный в [11; 14]. Этот метод позволяет, зная представления подгруппы, получить представления всей группы в виде блочно построенной матрицы. Студентами получено описание таблицы характеров для группы Фробениуса метациклического типа в общем виде и построены примеры для групп 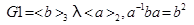 и
и 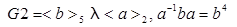 . Приведем полученную таблицу для G2.
. Приведем полученную таблицу для G2.
Таблица характеров для G2
|
Образующий элемент |
1 |
|
|
|
|
Порядок элемента Характеры |
1 |
5 |
2 |
2 |
|
c0 |
1 |
1 |
1 |
1 |
|
c1 |
1 |
-1 |
1 |
1 |
|
c2 |
2 |
0 |
|
|
|
c3 |
2 |
0 |
|
|
где 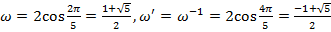 .
.
Результаты работы были представлены на студенческой конференции и опубликованы в сборнике студенческих работ. Во время презентации проекта кратко рассказано о теории представлений, поставленной задаче и выбранном методе решения. Полученное описание преставлений и таблицы характеров продемонстрированы на слайдах. На этом этапе у студентов формируются навыки грамотно излагать свои мысли доступным слушателю языком, применять в устной и письменной речи научные термины и использовать научный стиль изложения, умения быстро ориентироваться в материале, отвечать на вопросы аудитории. Подготовка доклада потребовала тщательной технической обработки таблиц и математических формул, освоения современных средств представления математических текстов, не ограничивающихся стандартными текстовыми редакторами.
Выводы
Таким образом, организация проектной деятельности бакалавров при изучении дисциплины «Алгебра» позволяет создавать образовательную среду, в которой учащиеся мотивированы на самостоятельный поиск научной информации и приобретают исследовательские умения (проектировочные, организаторские, коммуникативные и диагностические). Реализация проектов учащимися также повышает их мотивацию к освоению профильных математических дисциплин, позволяет глубже и эффективнее изучать материал. Курс алгебры позволяет устанавливать межпредметные связи с дисциплинами «Геометрия», «Математический анализ», «Информатика», «Экономика», «Иностранный язык». Работа над проектом способствовала формированию навыков научного исследования, создания нового знания, самостоятельного поиска информации, преодоления трудностей. При выполнении учебных проектов учитываются требования ФГОС ВО, так как у студентов формируются общекультурные, общепрофессиональные, профессиональные компетенции, необходимые для подготовки к педагогической, проектной и научно-исследовательской деятельности; а также конструктивные, проектировочные, организаторские, коммуникативные и диагностические умения.
Работа выполнена при финансовой поддержке ФГБОУ ВО «Шадринский государственный педагогический университет» по договору о выполнении НИР от 26.04.2018 г. № 145Н.
Библиографическая ссылка
Шумакова Е.О., Севостьянова С.А. ФОРМИРОВАНИЕ ПРОЕКТНЫХ УМЕНИЙ В УЧЕБНЫХ ПРОЕКТАХ БАКАЛАВРОВ ПО ПРОФИЛЬНЫМ МАТЕМАТИЧЕСКИМ ДИСЦИПЛИНАМ // Современные проблемы науки и образования. 2018. № 5. ;URL: https://science-education.ru/ru/article/view?id=28194 (дата обращения: 03.02.2026).