В последние годы с распространением компьютерных информационных технологий изменились роль и место математики в инфраструктурах человеческой деятельности: науке, технике, культуре, образовании, искусстве и т.д. Анализ влияния компьютерных информационных технологий и изменений в системе обучения в целом проводится с помощью сравнения советской и постсоветской системы обучения, например путем анализа научно-методической литературы [1], а также с помощью сравнительного анализа международного опыта обучения математике [2]. Интерес представляют предложения по изменению содержания курса математики и методик обучения [3-5].
Математические алгоритмы в основном внедрены в программное обеспечение профессиональной деятельности инженеров, экономистов и др., поэтому обучение их реализации этих алгоритмов «вручную» становится все менее актуальной задачей. Проблема существовала всегда, дать безусловно убедительный ответ на вопрос «понадобится ли мне умение решать тригонометрические уравнения, если я буду работать на заводе рабочим, мастером, снабженцем и т.п.?» не удавалось в любую эпоху. Заработанный математикой непререкаемый авторитет позволял до определенной степени подавлять возникающий протест против изучения традиционного содержания математических курсов (выражающийся, в частности, в чувстве тревоги при изучении математики [6]), но в настоящее время все сложнее найти аргументы в пользу обучения математике, убедительные для учащихся и для многих категорий студентов. Ясно, что отказ от систематического изучения математики приведет к общему падению науки, техники и культуры [7], и в последние годы делаются попытки фактически заменить курс математики обучением информатике или использованием готовых пакетов программ, таких как MathCAD, Mathematica, Maple [8]. Опыт использования соответствующих пакетов показывает необходимость разработки специальных методик обучения, иначе качество собственно математического образования не улучшается. Система обучения, наряду с системой здравоохранения, является самой консервативной, резкие перемены в которой чреваты тяжелейшими последствиями. Но это не отменяет необходимости продуманной осторожной корректировки, внедрения инноваций. Обычно использование информационных технологий рассматривается как инструмент обучения [9], а также как средство формирования определенных компетенций [10]. Итак, что остается от математики, если мы отказываемся от безусловного доминирования обучения ручного выполнения математических алгоритмов? В частности, какие цели математической деятельности придут на смену требованиям задачи, сформулированным как «найти площадь фигуры», «решить уравнение» и т.п. Или эти формулировки изменят смысл? Для этого следует предложить конструктивную трактовку понятия «цель деятельности», выделить приоритетные цели, обеспечить единое их понимание.
Материалы и методы
В качестве исходных материалов нашего исследования были выбраны, во-первых, учебники и задачники по различным разделам математики, во-вторых, специализированное математическое обеспечение для математических расчетов: Maxima, GAP, MathCAD, Mathematica, Maple и др., в-третьих, результаты анализа опыта преподавания математики учащимся и студентам. Основой методологии исследования послужила авторская теория моделирования Ю.Б. Мельникова [11], основанная на формально-конструктивной трактовке понятия «модель», включающая в себя теорию адекватности, «алгебру моделей» и др., а также разработки теории и методики обучения математике (в частности, деятельностный и компетентностный подходы).
Результаты исследования
Цель мы рассматриваем в рамках некоторой деятельности: и как один из инструментов планирования, и как составляющая средства оценивания адекватности результата деятельности. В случае когда цель рассматривается как инструмент планирования, для планируемого результата деятельности приоритетными оказываются эталонные модели, во-первых, грамматического характера (формы представления искомого объекта, правила оформления и др.) и, во-вторых, модели-шаблоны. В случае оценивания адекватности продукта деятельности проводится сравнение различных моделей этого продукта с соответствующими эталонами, т.е. моделями, принятыми за образец. Таким образом, использование цели для оценки результатов деятельности предполагает наличие системы эталонных моделей результата деятельности. Естественно считать, что эти эталонные модели изначально содержатся в составе цели. Поэтому цель в данной трактовке – модель, состоящая из таких эталонных моделей [12].
Обучение математической деятельности, основанное на трактовке цели как системы эталонных моделей результата деятельности, для каждой типовой цели требует контроля полноты ее состава, т.е. обучаемый (и преподаватель) должен знать все эталонные модели, входящие в состав этой цели. Кроме того, важно, чтобы обучаемые осознавали связи между этими эталонными моделями. В частности, как формирование интерфейсов для обмена информацией между моделями разных эталонных моделей можно рассматривать формирование и использование межпредметных связей [13].
В качестве инструмента контроля полноты состава цели мы предлагаем использовать различные классификации системы эталонных моделей в составе цели.
I. Если рассматривать систему эталонных моделей как множество с определенными отношениями между его элементами, то актуальными являются классификации, таксоны которых выделяются, во-первых, на основе анализа языка, на котором сформулирована эталонная модель, во-вторых, на оценке уровня общности эталонной модели, в-третьих, на количестве и особенностях связей между эталонными моделями в составе цели.
II. В деятельности можно выделить этапы планирования и реализации плана (они могут периодически сменять друг друга). Цель является одним из инструментов управления деятельностью, точнее, управления на стадии планирования.
Рассмотрим ситуацию, когда у исполнителя нет готового алгоритма, ассоциированного с приведенной формулировкой цели. Планирование в этом случае начинается с восприятия цели. Важной частью восприятия цели является выделение эталонных моделей, входящих в состав цели. Успех этой деятельности определяется, во-первых, эффективностью управления, во-вторых, наличием необходимых ресурсов.
Для контроля полноты состава конкретной цели математической деятельности мы предлагаем использовать следующую классификацию эталонных моделей в составе цели.
I. Классификация по структуре системы:
I.1) по языку теории; I.2) по уровню общности эталонной модели; I.3) по уровню субъективной или объективной многосвязности.
II. Классификация по особенностям деятельности с использованием цели:
II.4) по уровню ресурсоемкости восприятия или формирования эталонной модели (наглядности эталонной модели); II.5) по способу управления деятельностью; II.6) по характеру отношения субъекта деятельности к искомому математическому феномену.
Классификация эталонных моделей в составе цели по языку теории. C точки зрения языка теории рассмотрим, например, три способа задания вектора в геометрии: геометрический, символический и координатный. Геометрический способ мы можем использовать, когда нужно что-то просто «нарисовать». Например, изобразить вектор, перпендикулярный прямой, или коллинеарный заданному вектору. При этом нам не важны его числовые характеристики. Символический способ будет полезен, если вектор задаётся в виде комбинации некоторых известных векторов: с=3a+2b. Координатный способ задания вектора используется, когда вектор представляется в виде координат точки пространства или задача изначально формулируется в координатных терминах. В дополнение к этим трём способам задания вектора можно обозначить ещё один способ, по сути не являющийся геометрическим - геометрические преобразования с учётом субъекта деятельности. Например, требуется повернуть вектор на угол 90 градусов или отразить его относительно какого-либо геометрического объекта. Несмотря на то что данный способ основан на геометрической модели, его отличие заключается в том, что, во-первых, в данном способе присутствуют преобразования, во-вторых, используется активная роль субъекта, а не просто его геометрическая иллюстрация (в нашем случае – вектора).
Классификация эталонных моделей в составе цели по приоритетности (общности?) эталонной модели. Какие из эталонных моделей треугольника являются приоритетными? Как говорится: «С какой целью интересуетесь?». Обычно нам необходимо найти какие-то характеристики треугольника (например, периметр, площадь) или связанных с ним фигур (радиус вписанной или описанной окружности, длину высоты, биссектрисы или медианы и т.д.). Поэтому внешне-алгебраическое задание треугольника (как пересечение фигур, грань многогранника и др.) обычно менее интересно, чем внутренне-алгебраическое задание (по трем сторонам, двум сторонам и углу между ними, стороне и прилежащим углам). С этой точки зрения обычно предпочтительнее абсолютное задание величины (в единицах длины, градусах или радианах) по сравнению с относительным (сторона равна такому-то отрезку, в три раза больше и др.). Но если важен сам факт, что фигура является треугольником, и хоть какой-то образец, позволяющий каким-либо образом (пусть даже неудобным) идентифицировать треугольник, приоритетными могут оказаться другие эталонные модели. Например, этот тип моделей является приоритетным в теореме о подобии треугольников, образованных сторонами фиксированного треугольника и средними линиями, а также средними его линиями.
Классификация эталонных моделей в составе цели по уровню субъективной или объективной многосвязности. Если рассмотреть эталонные модели и классифицировать их по уровню субъективной и объективной многосвязности для модели «треугольник», то тут надо провести большое исследование, рассмотреть достаточное число целей, для которых известен их состав, выделить актуальные отношения между эталонными моделями с точки зрения «мегацели», частью которых является рассматриваемая цель.
В качестве «микроцели» («антоним» к мегацели) могут рассматриваться пункты плана достижения исходной цели, воспринятые исполнителем как цели деятельности, для которых не указан способ их достижения, или цель, являющаяся обобщением системы однотипных целей. Например, цель «найти длину радиуса вписанной окружности» является конкретизацией цели «найти длину отрезка», которая является конкретизацией цели «найти длину линии», потом – «найти величину фигуры», которая может трактоваться по-разному, например величину треугольника по-разному характеризуют и его площадь, и его периметр.
Классификация эталонных моделей в составе цели по уровню ресурсоемкости восприятия или формирования эталонной модели (наглядности эталонной модели). Например, рассмотрим эталонные модели плоскости, представленные в виде уравнений 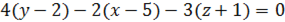 и
и  . Для того чтобы воспринять первое уравнение и интерпретировать его как уравнение плоскости, требуется больше усилий, чем для второго уравнения, поскольку, во-первых, вычисление выражения в левой части первого уравнения требует выполнения 5 операций «сложение» и трех операций «умножение чисел», а для второго уравнения – трёх операций «умножение» и только трёх операций «сложение чисел», во-вторых, для опознания «уравнения плоскости» для первого уравнения требуется перестановка слагаемых. С другой стороны, при попытке геометрической интерпретации первого уравнения не вызывает сложности выделение нормального вектора и начальной точки плоскости, для второго уравнения возникают некоторые сложности с вычислением какой-либо точки на плоскости.
. Для того чтобы воспринять первое уравнение и интерпретировать его как уравнение плоскости, требуется больше усилий, чем для второго уравнения, поскольку, во-первых, вычисление выражения в левой части первого уравнения требует выполнения 5 операций «сложение» и трех операций «умножение чисел», а для второго уравнения – трёх операций «умножение» и только трёх операций «сложение чисел», во-вторых, для опознания «уравнения плоскости» для первого уравнения требуется перестановка слагаемых. С другой стороны, при попытке геометрической интерпретации первого уравнения не вызывает сложности выделение нормального вектора и начальной точки плоскости, для второго уравнения возникают некоторые сложности с вычислением какой-либо точки на плоскости.
Классификация эталонных моделей в составе цели по способу управления деятельностью. Существует большое число классификаций управления деятельностью. Часто рассматривается прямое и косвенное управление. В первом случае управление осуществляется посредством ссылок на известные алгоритмы. Во втором случае – при косвенном управлении – планирование осуществляется посредством предоставления ресурсов и ограничений, в частности определяемых целью деятельности (ограничения могут касаться применяемых методов, времени исполнения и др.). Например, задания «найти… используя…» и «найти… не применяя…» отличаются именно характером управления. Примером эталонной модели функции, ориентированной на прямое управление деятельностью в случае цели «найти значение функции…», является задание функции явной формулой, скажем, f(x)=1+2x. На косвенное управление в этом случае ориентировано неявное задание функции, допустим, f(x)+xcos(f(x))=1 или задание функции, использующее разные значения аргумента, допустим, f(x)+xf(x+1)=f(x2)+5.
Классификация эталонных моделей в составе цели по характеру отношения субъекта деятельности к искомому математическому феномену. Типовые цели, представленные требованием задачи, определяются актуальными вариантами отношения к математическим феноменам [14]: 1) как к предмету деятельности и 2) как к инструменту деятельности. В случае когда феномен рассматривается как предмет деятельности, мы имеем: 1а) начальное состояние предмета; 1б) требуемое состояние предмета; 1в) реально полученное состояние предмета; 1г) процесс преобразования (описанный, например, в виде последовательности преобразований и др.). В случае когда феномен рассматривается как средство (инструмент) деятельности, мы имеем: 2а) предназначение инструмента; 2б) варианты (способы) применения и принцип действия; 2в) устройство инструмента.
Даже задачи с требованием, вполне традиционным для математической задачи, на самом деле могут носить не вычислительный характер. В качестве примера рассмотрим задание «найти сумму функции f, заданной таблицей значений
|
t |
0 |
1 |
2 |
3 |
4 |
|
f(t) |
-1 |
2 |
1 |
-3 |
-2 |
и функции g(x)=x2». Решение этой задачи основано на использовании типовых моделей объекта «функция» на осознанном применении интерфейсного компонента различных типовых моделей функции (совокупность числовых элементов первой строки является областью определения функции и т.д.).
|
s |
0 |
1 |
2 |
3 |
4 |
|
f(s)+g(s) |
-1 |
3 |
5 |
6 |
14 |
Результатом применения описанного аппарата являются задачи из системы разработанных нами интерактивных именных заданий (более 500 генераторов учебных заданий), разработанных в тестовой форме с автоматической генерацией заданий и автоматической проверкой их выполнения.
Обсуждение и заключения
Из сказанного выше следует, что представление цели как системы эталонных моделей результата деятельности является конструктивным и открывает новые перспективы в области теории, методики и практики обучения. Приведенные примеры подтверждают мысль о важности формирования максимально полного состава цели (с учётом уровня развития обучаемых). Контролируемое формирование состава цели позволяет начинать решение задачи с многопланового, многогранного представления об искомом объекте, что позволяет обучаемому успешно справляться с непривычными для него задачами. Предложенные в работе варианты классификации эталонных моделей результата деятельности можно использовать для контроля полноты состава цели, что позволяет совершенствовать деятельность и преподавателя, и обучаемого, улучшать результаты обучения, эффективно обучать управлению математической деятельностью. Остается открытым вопрос об оптимальном соотношении типов требований в учебных задачах (видов эталонных моделей, на которые ориентировано конкретное требование) в зависимости от категории обучаемых и условий обучения. Желательно составить справочник по составу типовых целей (на начальном этапе – наиболее распространенных), которые используют авторы учебных задач по математике при формулировке требований к этим задачам. Это важно как для преподавателей, так и для разработчиков учебно-методического обеспечения, поскольку позволит организовать контролируемый процесс усвоения состава соответствующих целей не только обучаемыми, но и педагогами.
Библиографическая ссылка
Мельников Ю.Б., Соловьянов В.Б. МОДЕЛИРОВАНИЕ ЦЕЛЕЙ УЧЕБНО-МАТЕМАТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ В ИНФОРМАЦИОННОМ ОБЩЕСТВЕ // Современные проблемы науки и образования. 2018. № 5. ;URL: https://science-education.ru/ru/article/view?id=28126 (дата обращения: 15.02.2026).
DOI: https://doi.org/10.17513/spno.28126



