В конце XX – начале XXI века среди жителей Российской Федерации получили широкое распространение заболевания сердечно-сосудистой системы [1]. Удельный вес случаев атеросклеротического поражения аорты, ее диссекции или аневризматической трансформации составляет 1/5 всех сосудистых заболеваний [2, 3]. Хирургическое лечение остается единственным эффективным способом оказания медицинской помощи (МП) пациентам с заболеваниями аорты [4, 5]. В последние годы эндоваскулярное лечение занимает лидирующие позиции в лечении пациентов с патологией аорты. Тактика оказания МП зависит от выраженности и протяженности патологического процесса. В зависимости от этих параметров предложены довольно громоздкие алгоритмы выбора тактики лечения. В связи с этим сосудистые хирурги зачастую отказываются от неудобных в практическом здравоохранении диагностических схем оказания МП больным с заболеваниями аорты [6]. Вместе с тем современная медицинская наука и практика делают возможными точную диагностику и прогнозирование хода патологического процесса благодаря применению прикладных компьютерных программ [7]. Компьютерное моделирование кровотока в просвете артерий позволяет не только оценить нарушения гемодинамики вследствие патологических изменений сосудистой стенки, но и спрогнозировать скорость прогрессирования заболеваний аорты и других периферических артерий, а также оценить риск разрыва при их аневризматической трансформации. Решение задачи математического моделирования кровотока в аневризматически измененной аорте имеет важное научно-практическое значение: оценка параметров гемодинамики позволит не только прогнозировать течение патологического процесса, но и осуществлять аргументированный выбор способа хирургического лечения [8].
Цель работы: на основании биомеханических технологий моделирования кровообращения определить варианты оценки математических моделей кровотока в аорте на примере ее аневризматического расширения, а также при имплантации в нее голометаллического стента.
Материалы и методы
Из раздела анатомии нижней конечности была выбрана геометрия самого крупного сосуда в организме – аорты. Для построения модели этого кровеносного сосуда потребовалось упростить его геометрию. Основные упрощения: жесткое закрепление аорты; внутренняя поверхность сосуда — идеально изолированная стенка; текучая среда — кровь (неньютоновская жидкость); давление в аорте 10 кПа; скорость кровотока в аорте 400 см/c; поток жидкости — ламинарный.
При работе в программе SolidWorks-2013 введены геометрические примитивы, из которых построена элементарная геометрическая модель аорты (рис. 1).
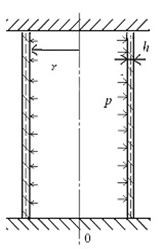 а
а 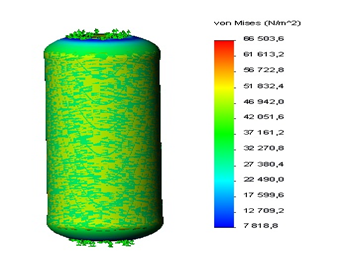 б
б
Рис. 1. Модель аорты: а – схема, б – распределение напряжений на схеме 3-мерного тела
При расчетах схем аневризм аорты (АА) были осуществлены несколько упрощений. АА интерпретировалась как 3-мерное тело; ее структура характеризуется изотропностью; стенка однослойная; купол АА симметричный; напряжения в АА в начале отсутствуют. Расчеты осуществлялись с применением метода конечных элементов (КЭ) с последующим разделением АА на большое количество (до 80 000) тетраэдальных элементов. На рисунке 2 представлена модель АА на криволинейном участке аорты, построенная с помощью метода КЭ.
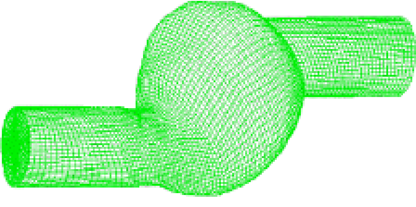
Рис. 2. Модель АА на криволинейном участке аорты, построенная с помощью метода КЭ
Данная модель построена при следующих значениях геометрических параметров аорты: диаметр сосуда (Dс) = 2,5 см, толщина стенки сосуда (hс) = 0,2 см, длина (Lс) = 30 см, модуль нормальной упругости сосуда (Ес) = 1,0 МПа, коэффициент Пуассона (ν) = 0,4; критическое напряжение в стенке аорты (σкр) = 0,7х106 Па; коэффициент запаса (k) = 2,5.
В процессе работы осуществлена оценка гемодинамических показателей в аневризматически измененной аорте на прямолинейном и криволинейном участках при различных параметрах ряда показателей: диаметр аневризмы (Dа), толщина ее стенки (hа), протяженность аневризмы (Lа), модуль упругости аневризмы (Еа).
Обсуждение результатов
Зависимости экстремальных значений напряжений (ЭН) и перемещений в сегментах аневризматически измененной аорты от механических свойств АА и ее геометрических параметров при артериальном давлении p=1,6х104 Па представлены на рисунках 3–6.

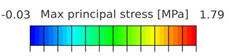
Рис. 3. Распределение ЭН σ в АА на прямолинейном участке аорты:
Lа=19 мм; Hа=16 мм; hа=2,0 мм; Ес=1,0 МПа; Еа=0,46 МПа; p=1,6 х 10 кПа
Зависимость экстремальных напряжений (ЭН) в стенке аневризматического расширения аорты, расположенного на прямолинейном сегменте, от толщины ее стенки представлена на рисунке 4.
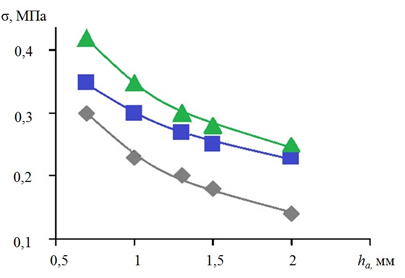
Рис. 4. Зависимости ЭН σ на прямолинейном участке аорты с аневризмой от толщины стенки: Ес=1,0 МПа; p=1,5х10 кПа;
Lа=19 мм; ν=0,4 (Еа:  – 1,0;
– 1,0;  – 0,5;
– 0,5;  – 0,25 МПа)
– 0,25 МПа)
В прямолинейном сегменте аорты констатируется обратная зависимость между толщиной стенки аневризматического мешка и критическим напряжением в его стенке вне зависимости от значения модуля упругости аневризмы. При толщине стенки 2 мм при значении Еа=1,0 МПа показатель σ составляет не более 0,2 МПа, при показателях модуля упругости АА 0,5 и 0,25 МПа ЭН соответственно составляет 0,28 и 0,3 МПа. Вне зависимости от толщины стенки АА в пределах 0,7–1,5 мм и значений Еа в диапазоне от 0,25 до 1,0 Мпа экстремальное напряжение стенки составляет не более 0,5 МПа, т.е. не превышает уровень критического напряжения (КН).
Зависимость показателя σ в стенке аневризматического мешка, расположенного на криволинейном участке аорты, от толщины его стенки приведена на рисунке 5.
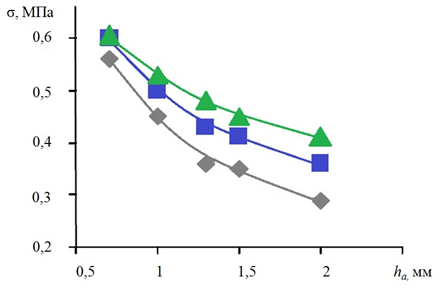
Рис. 5. Зависимости ЭН σ в АА на криволинейном участке от толщины ее стенки:
Ес=1,0 МПа; p=1,5х10 кПа; Lа=19 мм; ν=0,4 (Еа:  – 1,0;
– 1,0;  – 0,5;
– 0,5;  – 0,25 МПа)
– 0,25 МПа)
В сегменте аорты в области изгиба отмечается корреляция, аналогичная показателям кровотока на прямолинейном участке, однако при толщине стенки 1,5 мм показатели ЭН стенки аневризмы достигают показателей 0,5 МПа, а при истончении сосуда до 0,7 мм уже возникает критическое состояние, характеризующееся увеличением ЭН стенки до 0,6 МПа с риском ее разрыва.
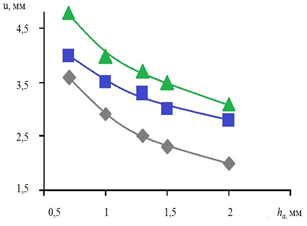
Зависимости перемещений u в АА на прямолинейном и изогнутом сегментах сосуда от толщины стенки сосуда приведены на рисунке 6.
 а
а 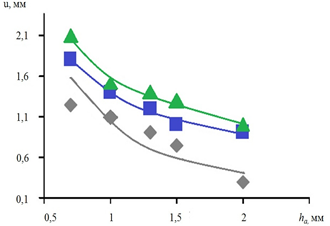 б
б
Рис. 6. Зависимости перемещений u в АА на прямолинейном и изогнутом
сегментах сосуда от толщины стенки сосуда: Ес=1,0 МПа; p=1,5х10 кПа;
Lа=19 мм; ν=0,4 (Еа:  – 0,25;
– 0,25;  – 0,5;
– 0,5;  – 1,0 МПа)
– 1,0 МПа)
В прямолинейном сегменте аорты при значениях модуля упругости АА 0,5–1,0 МПа критическое напряжение развивается при уменьшении толщины стенки АА до 0,5 мм, а при показателе модуля упругости аневризматического расширения сосуда 0,25 МПа критическое напряжение возникает при толщине стенки АА менее 1 мм. Критическое напряжение в аневризме на изогнутом сегменте аорты констатируется во всем диапазоне анализируемых параметров. На участках с показателями: протяженность АА 20 мм; толщина стенки АА 0,7 мм; модуль нормальной упругости сосуда 1,0 МПа; коэффициент Пуассона 0,4: при изменении диаметра АА в пределах 10–20 мм на прямолинейном участке сосуда при значениях модуля упругости аневризмы 0,25–1,0 МПа критическое напряжение не возникает. При оценке параметров кровотока на криволинейном участке КН возникает во всем диапазоне рассмотренных параметров.
Математическое моделирование позволяет создавать модели стентов, которые возможно имплантировать в аневризматически измененную аорту для предотвращения ее дальнейшего расширения и разрыва, проводить моделирование кровотока в аорте после выполнения эндоваскулярной коррекции (рис. 7).
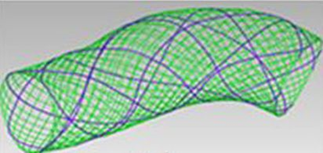
Рис. 7. Конечно-элементная модель голометаллического стента
При введении в условия создания модели параметров наличия металлического стента в просвете аневризматически измененной аорты характеристики кровотока приближались к стандартным показателям кровотока в указанном сосуде. Параметры экстремальных напряжений в области аневризматически измененной аорты приближались к показателям, представленным на рисунке 4, т.е. фактически напряжения стенки сосуда оставались в пределах физиологической нормы. Указанное обстоятельство свидетельствовало о положительном влиянии эндоваскулярного устройства на течение и, как следствие, на прогнозы анализируемого патологического состояния.
Таким образом, проведенные исследования выявления критического состояния аневризматического расширения аорты определяют необходимость предоперационного анализа данных с использованием компьютерного моделирования.
Заключение
Разработанная методика оценки состояния аорты представляется перспективной в плане деятельности сосудистых хирургов и ангиологов. Несмотря на то что полученные результаты компьютерного моделирования кровотока в аорте по большому счету общеизвестны, ряд показателей гемодинамики оказывается не столь очевидным, периодически вступая в некоторое противоречие с существующими представлениями о ее характеристиках в самом крупном сосуде организма. Атеросклеротическое и аневризматическое поражение аорты наряду с нарушением гемодинамических параметров в самом сосуде самым негативным образом отражается на характеристиках перфузии кровью всего организма. В связи с этим применение современных компьютерных технологий и биомеханики является абсолютно оправданным. Специалисты в области сосудистой хирургии нуждаются в программном обеспечении, которое позволит на основе ряда параметров, вносимых в программу, автоматически прогнозировать возможный результат различных видов хирургического или консервативного лечения. Это становится возможным посредством моделирования кровотока в артериальных сосудах. Применение компьютерных технологий оценки гемодинамики позволит обоснованно расставлять приоритеты в оказании медицинской помощи пациентам с заболеваниями аорты и других артериальных сосудов, что самым позитивным образом должно сказаться на качестве лечебно-диагностического процесса у больных сосудистого профиля.
Библиографическая ссылка
Чернявский М.А., Артюшин Б.С., Чернов А.В., Чернова Д.В., Жердев Н.Н., Кудаев Ю.А., Глушаков Д.Г., Теличкань В.С. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ В ОЦЕНКЕ ГЕМОДИНАМИЧЕСКИХ ПОКАЗАТЕЛЕЙ ПОСЛЕ ИМПЛАНТАЦИИ СТЕНТА ПРИ ПАТОЛОГИИ АОРТЫ // Современные проблемы науки и образования. 2018. № 5. ;URL: https://science-education.ru/ru/article/view?id=28070 (дата обращения: 15.02.2026).



