Среди проблем российского высшего образования [1-2] продолжает активно обсуждаться использование единого государственного экзамена (ЕГЭ) [3] как в системе аттестации школьных знаний, так и оценивания качества набора абитуриентов в высшую школу [4]. При оценке результатов подобного педагогического эксперимента необходимым является использование статистических методов [5-7]. При этом диапазон применения методов математической статистки достаточно широк: от оценивания влияния довузовской подготовки на успеваемость студентов вуза [8] и оценки качества деятельности преподавателя вуза [9] - до оценивания качества деятельности научно-образовательных организаций [10].
Целью настоящей статьи является представление совокупности базовых математических методов статистической обработки результатов педагогического эксперимента и методики их применения на примере такого «педагогического эксперимента», как кластеризация российских вузов по направлению подготовки «Физика» (НПФ) в факторном пространстве показателей вступительных испытаний (ПВИ) года аналогично [11]. В данном случае объектами наблюдения являются российские вузы, измеряемые показателями качества набора [4].
Одним из основных ПВИ является средний балл зачисленных по результатам ЕГЭ, динамику которого отражает временная модель регрессионной линейной зависимости среднего балла ЕГЭ (рис. 1).
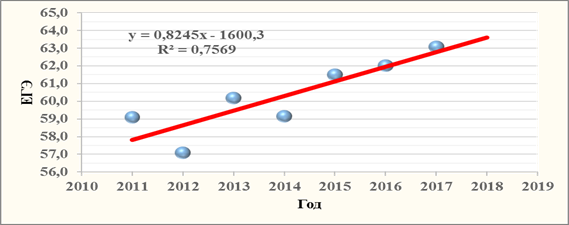
Рис. 1. Трендовая временная линейная регрессионная модель среднего балла ЕГЭ
Значение коэффициента корреляции Пирсона r равно 0,870 и статистически значимо (р» 0,011) отличается от ноля. Значение коэффициента детерминации r2 ≈0,757 ≥ 0,5. Следовательно, связь сильная, и уравнение регрессии применимо для прогноза.
Средний балл ЕГЭ характеризует выборку вузов как неоднородную (рис. 2).
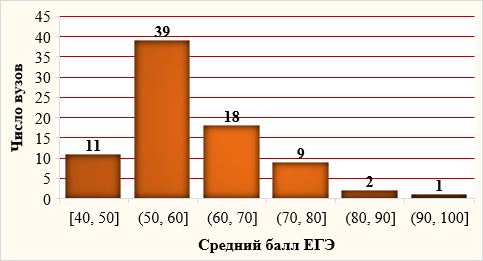
Рис. 2. Гистограмма вузов для ЕГЭ 2014 г.
Рейтинг качества приема в вузы по НПФ в 2014 году возглавляют технические университеты (ТУ): Московский физико-технический институт (МФТИ) имеет высший средний балл ЕГЭ – 92,6 по 100-балльной шкале, а национальный исследовательский (НИ) Московский ядерный университет (МИФИ) – на втором месте (86,8). Далее идут классические государственные университеты (ГУ): Московский (МГУ) – третий (82,4) и Санкт-Петербургский (СПбГУ) – четвертый (79,2). В первую десятку входит также Московский технический ГУ (МГТУ) – восьмой (75,1). Федеральные университеты (ФУ) расположены ниже: Уральский (УФУ) – 15-е место (67,5), Дальневосточный (ДФУ) – 46-е место (56,2), Северо-Кавказский (СКФУ) – 74-е место (47,1). Томские вузы НИ ТПУ и НИ ТГУ занимают по НПФ соответственно19-е (64,2) и 22-е (62,8) места среди 80 вузов.
Методика многомерного статистического анализа
В данной работе на основании базы данных качества приема в вузы по НПФ [4] использованы показатели вступительных испытаний (ПВИ) на примере 2014 г.: ЕГЭ; динамический показатель – разность ЕГЭ 2014 и 2013 гг. (Dегэ), средний балл ЕГЭ зачисленных по конкурсу 2014 в расчете на один предмет (ЕГЭк), балл самого слабого из зачисленных (ЕГЭм), количество зачисленных на бюджетные места (N), количество зачисленных по конкурсу (Nк), количество студентов, зачисленных по олимпиадам (Nо), а также доля студентов (в%), принятых по олимпиадам (Nо%). Можно обратить внимание на непопулярность олимпиадной формы вступительных испытаний (малость NО).
Каждый ПВИ можно исследовать средствами одномерного статистического анализа. Например, гистограмма ЕГЭ (рис. 2) близка к кривой нормального закона, но характеризуется положительной выборочной асимметрией (А = 0,866 > 0) и положительным выборочным эксцессом (Е = 1,06 > 0), т. е. островершинностью. По χ2-критерию Пирсона распределение ЕГЭ (рис. 2) слабо значимое (р» 0,045) отличается от нормального закона (средняя - 59,2 балла, стандартное отклонение - 10,3). Выборка ЕГЭ является 3-профильной, содержащей 22 ТУ, 56 ГУ и 2 педагогических университета (ПУ). Оценка значимости различий средних баллов ЕГЭ по профилям ТУ, ГУ и ПУ(63,7; 57,5 и 58,2 соответственно) в рамках однофакторного дисперсионного анализа на основе параметрического F-критерия приводит к слабо значимым (р» 0,054) различиям профильных средних по совокупности, которые смягчаются до незначимых (р» 0,146) на основе непараметрического критерия Краскела-Уоллиса. Учитывая отклонение распределения ЕГЭ от нормального закона (рис. 2), а в большей степени порядковый характер шкалы измерения ЕГЭ, можно считать выборку ЕГЭ однородной по профилям.
Для выбранных выше вузов значения всех ПВИ приведены в табл. 1.
Таблица 1
Фрагмент исходной базы данных (ПВИ по НПФ 2014 г.)
|
Ранг |
Вуз |
Профиль |
ЕГЭ |
Dегэ |
ЕГЭк |
ЕГЭм |
N |
Nк |
No |
No% |
|
1 |
МФТИ |
техн |
92,6 |
-0,4 |
93,6 |
67,3 |
768 |
652 |
36 |
4,69 |
|
2 |
МИФИ |
техн |
86,8 |
-0,9 |
86,8 |
82 |
45 |
42 |
2 |
4,44 |
|
3 |
МГУ |
клас |
82,4 |
-4,1 |
82,6 |
67,3 |
442 |
383 |
45 |
10,18 |
|
4 |
СПбГУ |
клас |
79,2 |
-3,2 |
79,2 |
61,7 |
180 |
133 |
46 |
25,56 |
|
8 |
МГТУ |
техн |
75,1 |
-2 |
76,9 |
56,7 |
40 |
27 |
9 |
22,50 |
|
15 |
УФУ |
клас |
67,5 |
4,5 |
67,8 |
46 |
74 |
71 |
0 |
0,00 |
|
19 |
НИ ТПУ |
техн |
64,2 |
-1,8 |
64,2 |
52,7 |
21 |
20 |
1 |
4,76 |
|
22 |
НИ ТГУ |
клас |
62,8 |
4,1 |
63,2 |
42,7 |
149 |
143 |
3 |
2,01 |
|
46 |
ДФУ |
клас |
57,9 |
-4,3 |
57,9 |
42,7 |
20 |
20 |
0 |
0,00 |
|
74 |
СКФУ |
клас |
47,1 |
-12,1 |
47,3 |
35,3 |
20 |
18 |
0 |
0,00 |
В данной работе использованы корреляционный, кластерный, факторный и дисперсионный анализы, проведенные в системе Statistica [7].
В первую очередь проведен корреляционный анализ ПВИ (табл. 2).
Таблица 2
Коэффициенты парных корреляций ПВИ (r - Пирсона и R – Спирмена)
|
ПВИ |
Dегэ |
ЕГЭ |
ЕГЭк |
ЕГЭм |
N |
Nк |
No |
No% |
|
|
Dегэ |
1,000 |
0,332 |
0,293 |
0,273 |
0,003 |
0,006 |
-0,071 |
-0,142 |
r |
|
ЕГЭ |
0,292 |
1,000 |
0,998 |
0,830 |
0,557 |
0,536 |
0,582 |
0,541 |
|
|
ЕГЭк |
0,337 |
0,998 |
1,000 |
0,825 |
0,555 |
0,534 |
0,578 |
0,540 |
|
|
ЕГЭм |
0,333 |
0,767 |
0,762 |
1,000 |
0,357 |
0,335 |
0,432 |
0,425 |
|
|
N |
-0,136 |
0,320 |
0,317 |
-0,041 |
1,000 |
0,997 |
0,706 |
0,312 |
|
|
Nк |
-0,124 |
0,298 |
0,291 |
-0,063 |
0,992 |
1,000 |
0,660 |
0,258 |
|
|
No |
-0,070 |
0,546 |
0,543 |
0,428 |
0,517 |
0,481 |
1,000 |
0,792 |
|
|
No% |
-0,079 |
0,545 |
0,541 |
0,429 |
0,496 |
0,457 |
0,997 |
1,000 |
|
|
R |
|||||||||
Жирным шрифтом в табл. 2 выделены наиболее значимые корреляции. Согласно табл. 2, на корреляционной основе можно выделить 4 группы ПВИ {Dегэ}, {ЕГЭ, ЕГЭк, ЕГЭм}, {N, Nк} и {Nо, No%}.
Во вторую очередь проведен кластерный анализ ПВИ. При этом использованы корреляционное расстояние 1 – r как мера близости ПВИ и метод Уорда в качестве правила объединения кластеров. Результат древовидной кластеризации ПВИ изображен на рис. 3, где выделены 4 корреляционно значимо различных кластера ПВИ: FD = {Dегэ}, FЕГЭ ={ЕГЭ, ЕГЭк, ЕГЭм}, FN = {N, Nк} и FNo ={Nо, No%}.
На основании наличия значимых корреляций ПВИ в третью очередь проведен факторный анализ ПВИ, позволяющий сократить число показателей и выделить новые факторные показатели, объединяющие корреляционно связанные ПВИ, выделенные жирным шрифтом в табл. 3.
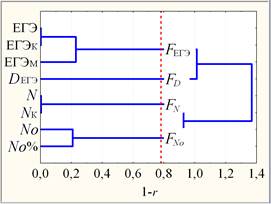
Рис. 3. Горизонтальная дендрограмма корреляционной матрицы ПВИ
(пунктирная прямая критического уровня:1-r = 0,78; n = 80)
Таблица 3
Факторные нагрузки ПВИ
|
Таким образом, построена 4-факторная модель ПВИ, объясняющая их изменчивость на 96,5%. На основании высоких факторных нагрузок ПВИ (табл. 3) построена интерпретация факторов:
Фактор_1 (FЕГЭ) – наиболее весомый (0,328), характеризуется ЕГЭ, ЕГЭк и ЕГЭм, связанными положительной корреляционной связью, и интерпретируется как фактор качества приема в вузы по НПФ.
Фактор_2 (FN) – менее весомый (0,296), характеризуется N и Nк, связанными положительной корреляционной связью, и интерпретируется как фактор количества приема в вузы по НПФ.
Фактор_3 (FNo) – еще менее весомый (0,212), характеризуется Nо и No%, связанными положительной корреляционной связью, и интерпретируется как фактор креативности приема в вузы по НПФ.
Фактор_4 (FD) – наименее весомый (0,129), характеризуется Dегэ и интерпретируется как фактор динамики качества приема в вузы по НПФ.
Особенностью данной базы данных (ПВИ) является то, что 80% вузов имеют нулевой результат по No. Поэтому, согласно табл. 3, из соображения наглядности в качестве фактора креативности Ф3 использовано ниже среднее арифметическое стандартизированных значений No и No%. В качестве фактора количества Ф2 использовано стандартизированное значение N. Размерность построенного факторного пространства ПВИ можно снизить, используя в качестве фактора качества Ф1 среднее арифметическое стандартизированных значений ЕГЭ 2014 и 2013 гг. вместо FЕГЭ и FD.
В четвертую очередь проведен кластерный анализ вузов в пространстве {Ф1, Ф2, Ф3}. При этом выбрано расстояние Чебышева как мера близости и метод Уорда в качестве правила объединения кластеров. Можно построить кластерную модель вузов, соответствующую выбранному расстоянию объединения. Так, например, 11-кластерная модель (К1–К11) соответствует расстоянию объединения, равному 2,5, а 8-кластерная модель (К1, К2, К3, К4+К5, К6+К7, К8, К9, К10+К11) соответствует расстоянию объединения, равному 4.
В пятую очередь проведен дисперсионный анализ качества 11-кластерной модели 80 вузов по НПФ. В результате выявлены высоко значимые (р < 0,0005) различия между 11 кластерами вузов как по совокупности 3 факторов, так и по каждому фактору (рис. 4).
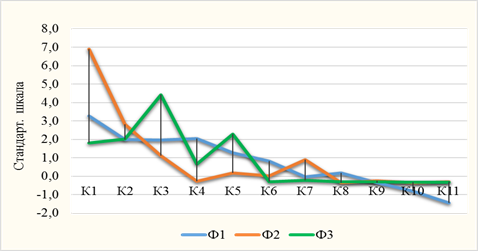
Рис. 4. Графики средних кластеров вузов
Дисперсионный анализ позволяет выделить для каждого фактора однородные группы кластеров:
Ø Ф1: {К1}, {К4, К2, К3}, {К5, К6}, {К8, К7}, {К9}, {К10}, {К11}.
Ø Ф2: {К1}, {К2}, {К3, К7}, {К5, К6}, {К9, К4, К11, К8, К10}.
Ø Ф3: {К3}, {К5, К2, К1}, {К4}, {К7, К6, К8, К9, К11, К10}.
В шестую очередь на основании результатов кластерного анализа вузов проведена их классификация по номинальной шкале (табл. 4).
Таблица 4
Классификация вузов по НПФ в номинальной шкале
|
Кластер (число вузов) |
Примеры вузов |
Уровень кластера по факторам |
||
|
Ф1(ЕГЭ) |
Ф2(N) |
Ф3(NО) |
||
|
К1(1) |
МФТИ |
Лидер |
Лидер |
Выше среднего |
|
К2(2) |
МГУ |
Выше среднего |
Лидер |
Выше среднего |
|
К3(2) |
СПбГУ |
Выше среднего |
Выше среднего |
Лидер |
|
К4(3) |
МИФИ |
Выше среднего |
Ниже среднего |
Средний |
|
К5(2) |
МГТУ |
Средний+ |
Средний |
Выше среднего |
|
К6(9) |
УФУ |
Средний+ |
Средний |
Ниже среднего |
|
К7(3) |
НИ ТГУ |
Средний |
Выше среднего |
Ниже среднего |
|
К8(13) |
НИ ТПУ |
Средний |
Ниже среднего |
Ниже среднего |
|
К9(25) |
ДФУ |
Средний– |
Ниже среднего |
Ниже среднего |
|
К10(13) |
СКФУ |
Ниже среднего |
Ниже среднего |
Ниже среднего |
|
К11(7) |
Аутсайдер |
Ниже среднего |
Ниже среднего |
|
Выводы
1. Рассмотрена методика применения совокупности базовых математических методов статистической обработки экспериментальных данных на примере многомерного статистического анализа в системе Statistica качества набора абитуриентов в российские вузы по направлению подготовки «Физика» на основе результатов вступительных испытаний 2014 г.
2. На основании корреляционного анализа выявлены 4 группы ПВИ: {ЕГЭ, ЕГЭк, ЕГЭм}, {N, Nк}, {Nо, No%} и {Dегэ}, а с помощью факторного анализа построена 4-факторная модель ПВИ, объясняющая изменчивость ПВИ на » 96,5%. Выделенные факторы проинтерпретированы как факторы качества, количества, креативности и динамики приема в вузы по НПФ.
3. В рамках кластерного анализа в 3-мерном факторном пространстве {качества, количества, креативности} построена кластерная модель вузов с заданным числом кластеров. Подробно рассмотрена высококачественная 11-кластерная модель 80 вузов, выделены группы однородных кластеров для каждого факторного показателя.
4. Построена временная модель регрессионной линейной зависимости среднего балла ЕГЭ (коэффициент детерминации r2 ≈0,757), характеризующая статистически значимый положительный тренд среднего балла ЕГЭ на периоде 2011-2017 гг.
Библиографическая ссылка
Арефьев В.П., Михальчук А.А., Филипенко Н.М., Задорожный В.Н. МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ КАЧЕСТВА НАБОРА АБИТУРИЕНТОВ В РОССИЙСКИЕ ВУЗЫ ПО НАПРАВЛЕНИЮ ПОДГОТОВКИ «ФИЗИКА» // Современные проблемы науки и образования. 2018. № 2. ;URL: https://science-education.ru/ru/article/view?id=27530 (дата обращения: 16.02.2026).



