Инструментом исследования во многих сферах человеческой деятельности выступают математические модели, характерным свойством которых является общность по отношению к изучаемым объектам. Важно то, что одна и та же модель может описывать процессы различной природы [1-3].
В.А. Штофф под моделью понимает «…такую мысленно представляемую или материально реализованную систему, которая, отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает новую информацию об объекте» [4, с. 22].
Математическое моделирование – мощный метод познания внешнего мира, а также прогнозирования и управления. Метод математического моделирования сводит исследование явлений внешнего мира к математическим задачам. Математические модели стали необходимым аппаратом в области экономического планирования.
Выделяют следующие классы экономико-математических моделей: макроэкономические, микроэкономические, балансовые, теоретические, практические, статические, динамические, детерминированные, оптимизационные, стохастические [5; 6].
Процесс математического моделирования включает три этапа: построение модели, внутримодельное решение, интерпретация ответа.
Знакомить учащихся с основными понятиями и видами деятельности в экономической сфере можно в процессе обучения математике, решая экономические задачи [7].
Покажем на примерах, каким образом можно экономические задачи решить средствами Mathcad и Maple и дадим дидактико-методические рекомендации по использованию этих средств.
Тема «Линейная функция»
Задача 1. Постоянные издержки при производстве ручных часов составляют 12000 рублей в месяц, а переменные – 300 рублей за один час. Цена часов 500 рублей. Написать функции дохода и издержек. Построить графики. Найти точку безубыточности. (Точкой безубыточности называют точку, в которой прибыль обращается в нуль.)
Тема «Квадратичная функция»
Задача 2. При производстве табуреток производитель закупает древесину у поставщика. Поставщик делает незначительные скидки при увеличении объема закупки, в результате стоимость древесины составляет p=100-0,001q, где p – цена 1 единицы, ден. ед.; q – объем продаж поставщика, м3. Затраты по заготовке и хранению древесины составляют C(q)=550+40q. При каком объеме продаж можно достичь максимальной прибыли?
Заметим, что прибыль П равна разности между выручкой (полным доходом) U и затратами (полными затратами) С , то есть П=U – С . Выручка U равна произведению цены p за единицу товара на количество проданных единиц товара x: U(x) = p · x.
Цена p зависит от спроса и p(x) = ax + b , причем a<0. Тогда U(x) = px = (ax+b)·x = ax2 + bx – это парабола, у которой ветви направлены вниз.
Полный доход достигает максимального значения при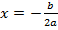 
.
Тема «Система линейных уравнений»
Задача 3. В таблице 1 приведены расценки на выполнение работ для каждого вида оборудования. Найдите расчетные объемы работ (количество часов использования оборудования), которые смогут окупить затраты на эксплуатацию.
Таблица 1
Расценки на выполнение работ для различных видов оборудования
|
Виды работ |
Нормативы по видам оборудования, ден. ед. |
Полные затраты на эксплуатацию, ден. ед. |
||
|
механическое |
тепловое |
энергетическое |
||
|
Техническое обслуживание |
3 |
1 |
4 |
85 |
|
Текущие услуги |
2 |
2 |
3 |
82 |
|
Капитальный ремонт |
10 |
20 |
15 |
580 |
Тема «Дифференцирование функции одной переменной»
Задача 4. Себестоимость производства телевизоров y (тысяч руб.) описывается функцией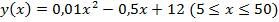 
, где x – объем выпускаемой продукции в месяц (тыс. ед.). Определить скорость и темп изменения себестоимости при выпуске 20 и 40 тыс. ед. продукции.
Рассмотрим задачи линейного и нелинейного программирования.
Задача 5. Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы продуктов даны в таблице 2. Требуется определить количество мороженого каждого вида, которое должна производить фирма, чтобы доход от реализации продукции был наибольшим.
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более, чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена одного килограмма сливочного мороженого 16 у.е., шоколадного – 14 у.е.
Решение. Обозначим: 
– суточный объем (в кг) выпуска сливочного мороженого, 
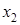– аналогичный объем шоколадного. Составим математическую модель задачи.
Таблица 2
Расход продуктов на изготовление различных сортов мороженого
|
Исходный продукт |
Расход на 1 кг сливочного |
Расход на 1 кг шоколадного |
Запас, кг |
|
Молоко |
0,8 |
0,5 |
400 |
|
Наполнители |
0,4 |
0,8 |
365 |
Целевая функция имеет вид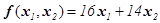 
. Система ограничений:
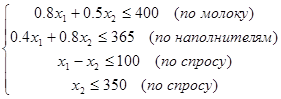
и, естественно,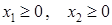 
. Укажем на рисунке допустимую область. В системе Maple в пакете расширения plots имеется специальная графическая функция inequal, которая на плоскости строит область, описываемую линейными неравенствами. Действие этой функции продемонстрируем на нашем примере.
Наберем такой текст:
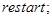
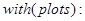
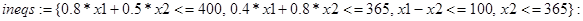
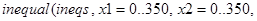
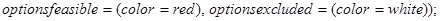
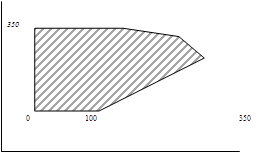
Здесь опция цветов optionfeasible задает цвет области, для которой удовлетворяются все неравенства; на экране она будет закрашена в красный цвет (red). Опция optionexcluded задает цвет внешности допустимой области; она согласно тексту документа закрашена в белый цвет (white), т.е. вообще не закрашена.
Графическое изображение допустимой области ограничений
Далее приступим к максимизации целевой функции. Подключим пакет решения задач линейной оптимизации simplex, зададим целевую функцию, используем встроенную функцию maximize. Закажем ее максимальное значение.
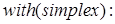
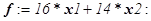
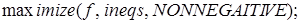
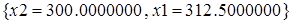
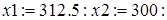
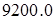
Нетрудно расшифровать последние строки документа: оптимальные объемы и наибольший доход: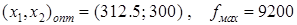 
.
А вот решение этой же задачи в системе Mathcad.
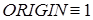
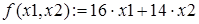
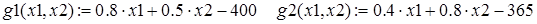
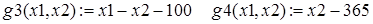
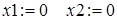
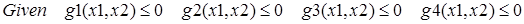
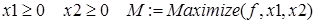
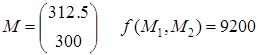
Обратимся далее к задаче нелинейного математического программирования: «задача о посылке», в решении которой тестируются различные методы оптимизации. Приведем эту задачу в двух вариантах.
Задача 6.
А. Стандартная задача. Посылка, которую должны отправить по почте, имеет форму ящика с размерами в дюймах:
.
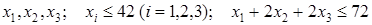При каких размерах объем посылки будет наибольшим?
Б. Модифицированная задача. Она аналогична задаче, приведенной выше, но ограничения немного другие:
.
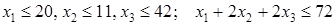Любители программирования на Бейсике могут найти решения в интересной работе [8]. Попытаемся решить в системе Mathcad модифицированную задачу.
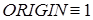
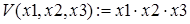
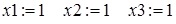
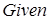
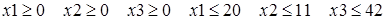
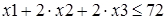
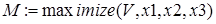
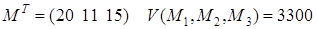
Как видно, Mathcad справился с решением задачи. А вот попытки решить ее в системе Maple не увенчались успехом.
В экономических исследованиях широко применяются так называемые производственные функции, выражающие зависимость результата производства от затрат ресурсов. В качестве ресурсов (факторов производства) на макроуровне обычно рассматривается накопленный труд в форме производственных фондов (капитал) K и живой труд L, а в качестве результата – валовой выпуск Y. Таким образом, используется в экономике модель вида: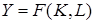 
.
Возникновение теории производственных функций принято относить к 1928 г., когда появилась статья американских ученых – экономиста П. Дугласа и математика Д. Кобба – «Теория производства», в которой эмпирическим путем определялось влияние затрачиваемого капитала и труда на объем выпускаемой продукции в обрабатывающей промышленности США по данным за
1899-1922 гг. Коббом была предложена мультипликативная производственная функция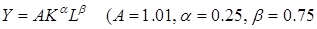 
).
Отечественные экономисты также занимались построениями производственных функций. Так, на основании данных по экономике Российской Федерации бывшего СССР за 1960-1994 гг. мультипликативная функция валового выпуска имела параметры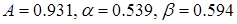 
.
Производственные функции являются основными элементами в различных моделях поведения производителей. В следующем примере рассмотрены основные задачи оптимизации производства для случая однопродуктовой двухресурсной мультипликативной производственной функции. Используются обозначения: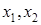 
– объемы используемых фирмой ресурсов, 
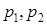– рыночные цены на эти ресурсы, 
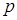– цена единицы выпускаемой продукции, 
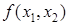– ее объем. Основными задачами в теории фирмы являются следующие.
1. Максимизировать прибыль – разность между выручкой от продажи продукции и затратами на приобретение ресурсов
.
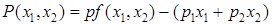2. При заданном ограничении на затраты найти комбинацию ресурсов, максимизирующую выпуск, т.е. решить задачу
.
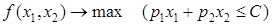3. При заданном объеме выпуска найти комбинацию ресурсов, обеспечивающую минимум затрат, – решить задачу
.
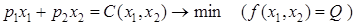Здесь переменные неотрицательные, в задачах 2 и 3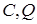 
– заданные положительные числа. Предполагая 
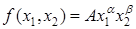, для компьютерного решения зададим конкретные значения параметров.
Учащимся может быть предложена следующая задача.
Задача 7. Решить задачи 1–3, учитывая условия:
.
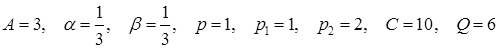В задаче 1 между переменными нет связи; имеем безусловную оптимизацию функции прибыли, которая строго вогнутая. Поэтому в единственной стационарной точке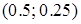 
имеется минимум, равный 
.
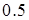В задаче 2 надо искать наибольшее значение выпуска в замкнутой области, описываемой неравенствами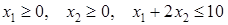 
. Так как стационарных точек нет, то максимум нужно искать на границе области, а именно на изокосте 
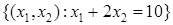. Геометрическое решение будет состоять в том, чтобы среди всех изоквант (линий уровня функции выпуска) выбрать ту, которая касается изокосты. Точка касания 
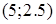– искомая; в этом легко убедиться, применяя метод Лагранжа. Максимальное значение выпуска приблизительно 6.962.
Задачу 3 также можно решить геометрически: среди изокост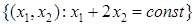 
выбрать ту, которая касается изокванты 
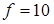. Минимум затрат, равный 8, достигается в точке 
.
Другие экономические задачи, решаемые в математических средах Mathcad и Maple, читатель найдет в наших работах [9; 10].
Выводы
Проведенный педагогический эксперимент в профильных экономических классах показал, что, работая с математическими пакетами Mathcad и Maple, учащиеся учатся использовать особенности этих пакетов в решении экономических задач линейного и нелинейного программирования, приобретают умения по работе с таблицами и графическим материалом, который имеет важное значение в работе экономистов, овладевают умением визуализировать различную экономическую информацию и статистическими методами обрабатывать различного рода экономические результаты.
Библиографическая ссылка
Далингер В.А. ОБУЧЕНИЕ УЧАЩИХСЯ РЕШЕНИЮ ЭКОНОМИЧЕСКИХ ЗАДАЧ В МАТЕМАТИЧЕСКИХ СРЕДАХ MATHCAD И MAPLE // Современные проблемы науки и образования. – 2018. – № 2. ;URL: https://science-education.ru/ru/article/view?id=27529 (дата обращения: 18.04.2024).