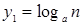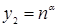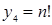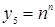Компетентностный подход является основным направлением повышения качества высшего образования. В современных образовательных стандартах цели обучения сформулированы в виде списка компетенций, определяющих дальнейшую адаптацию выпускника в обществе. Специалист должен уметь применять полученные знания в своей профессиональной деятельности и в различных жизненных ситуациях [1].
Основываясь на определениях образовательной компетенции и компетентности, предложенных А.В. Хуторским [2], под математической компетенцией мы понимаем совокупность взаимосвязанных качеств личности, включающих математические знания, умения, навыки, способы мышления и деятельности, а также способность приобретать новые математические знания и использовать их в дальнейшей профессиональной деятельности. Математическая компетентность есть результат освоения математической компетенции, ее практическая реализация.
Активизация самостоятельной работы студентов – ключевое направление повышения математической компетентности. Составляющими компонентами учебной деятельности являются индивидуальное планирование, самоорганизация, саморазвитие, самооценка, представление и защита своих учебных достижений. Студент становится субъектом обучения, с помощью преподавателя добывающим свои знания. При этом коренным образом меняется и роль преподавателя. Из информатора, носителя знаний он становится помощником, организатором деятельности обучаемых.
Достижение определенного уровня математической компетентности представляет собой целевую категорию, задающую направленность разрабатываемых учебных программ. Ориентация на сформулированные цели влияет на отбор содержания обучения и обуславливает необходимость поиска критериев, методов и средств оценки нового образовательного результата. Кроме того, появляется необходимость в качественной оценке, во включении в процедуру оценивания наблюдения за деятельностью студентов.
Рассмотрим принципы обучения математике, целью которого является повышение математической компетентности бакалавров. Разработка этих принципов основана на анализе компонентов адаптивной системы обучения А.С. Границкой [3], опыта работы педагогов средней школы, использующих эту систему в своей работе, начиная с восьмидесятых годов прошлого века, а также собственного педагогического опыта.
· Распределение времени при построении семинара.
Время, отведенное на самостоятельную работу студентов, составляет 60-80% практического занятия по математике. В течение 20-30 минут преподаватель объясняет новый материал, разбирает типовые задачи, составляет опорные схемы решения. Оставшееся время обучаемые работают в индивидуальном режиме, а преподаватель поочередно занимается с отдельными студентами, управляет самостоятельной работой.
· Организация деятельности студентов на семинаре.
При выполнении самостоятельной работы обучаемые работают в своем темпе, выполняют задания различного уровня сложности и требуют разную степень помощи преподавателя. Трудность задания и скорость его выполнения зависит от таких факторов, как подготовленность, способность, работоспособность. Студентам предоставляется самим выбирать уровень сложности задания. Кроме того, каждый из них сам определяет, стоит ли ему переходить к решению более сложных задач. В результате такой организации и слабые, и сильные студенты обеспечены такими заданиями, которые соответствуют их текущему уровню подготовки. Все включены в активную самостоятельную работу. Роль студента изменяется от объекта к субъекту обучения. Он планирует свою деятельность, принимает решения, включен в ответственность за результат обучения и осознает его значимость.
· Отбор задач для самостоятельной работы.
Задания для самостоятельной работы разделены на несколько уровней сложности. В соответствии с поставленной целью их можно соотнести с уровнем математической компетентности. В методических рекомендациях для преподавателей вузов рекомендовано установить следующие уровни: пороговый, продвинутый, высокий [4]. Принцип отбора задач дает возможность поэтапного построения обучения, позволяющего повышать сложность выполняемых заданий постепенно. Кроме того, появляется возможность оценить компетентностный результат обучения [5].
· Использование моделей поэтапного решения математических задач.
В ходе практических занятий преподавателем и студентами совместно создаются модели поэтапного решения типовых заданий, опорные схемы, обобщающие таблицы, которые впоследствии используются в самостоятельной работе.
Рассмотрим фрагмент семинара, на котором рассматриваются задачи на исследование сходимости ряда с помощью признаков сравнения рядов с положительными членами.
Признаки сравнения служат для исследования вопроса о сходимости данного ряда с помощью вспомогательного ряда. Поэтому решение задачи разбивается на несколько этапов:
1) выбор вспомогательного ряда;
2) исследование сходимости вспомогательного ряда;
3) установление связи между соответствующими членами данного и вспомогательного рядов («мостик»);
4) применение признака сравнения для вывода о сходимости данного ряда.
При выборе вспомогательного ряда, как правило, из выражения общего члена данного ряда отбрасываются второстепенные элементы. Для успешного решения этой задачи необходимо уметь правильно оценить, какими элементами определяется поведение общего члена ряда. В этой работе очень полезной является информация о скорости возрастания элементарных функций при 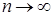 , приведенная в таблице, в которой основные элементарные функции расположены слева направо в порядке увеличения скорости возрастания при
, приведенная в таблице, в которой основные элементарные функции расположены слева направо в порядке увеличения скорости возрастания при 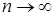 .
.
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
Если 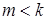 , то
, то  для любой пары функций из этой таблицы. С помощью этих данных можно безошибочно установить, какие элементы являются «главными» в выражении общего члена исследуемого ряда.
для любой пары функций из этой таблицы. С помощью этих данных можно безошибочно установить, какие элементы являются «главными» в выражении общего члена исследуемого ряда.
При выборе вспомогательного ряда необходимо учитывать требование достаточной простоты, важное при исследовании на сходимость. Такими простыми «эталонными» рядами являются:
ряд, составленный из членов геометрической прогрессии 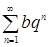 ,
,
если 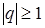 – ряд расходится, если
– ряд расходится, если 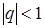 – ряд сходится;
– ряд сходится;
и обобщенный гармонический ряд 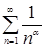 , если
, если 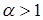 – ряд сходится, если
– ряд сходится, если 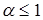 – ряд расходится.
– ряд расходится.
Пример. Исследовать на сходимость ряд 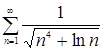 .
.
Решение.
1. Поведение общего члена ряда определяется слагаемым 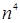 . Отбрасывая остальное, получаем вспомогательный ряд
. Отбрасывая остальное, получаем вспомогательный ряд 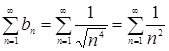 .
.
2. Это обобщенный гармонический ряд 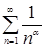 ,
,  , следовательно, ряд сходится.
, следовательно, ряд сходится.
3. Находим «мостик»
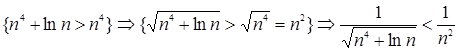 .
.
4. Решение задачи завершает логическая цепочка:
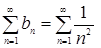 сходится,
сходится, 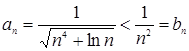
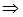
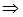 ряд
ряд 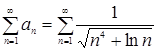 сходится по первому признаку сравнения.
сходится по первому признаку сравнения.
Решение данной задачи можно записать в виде опорной схемы, которая в дальнейшем будет использоваться при решении подобных задач.
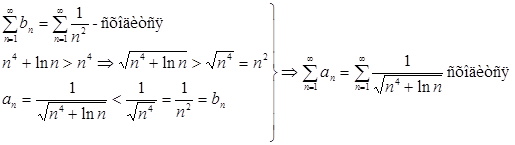
· Управление учебной деятельностью.
Активная самостоятельная деятельность управляется с помощью сетевого плана – графической модели учебного процесса. Имея такую модель, студент видит весь объем работы, который ему необходимо выполнить в определенном модуле данной дисциплины.
Процесс конструирования модульного сетевого плана состоит из нескольких этапов. На первом этапе преподаватель рассчитывает время, отведенное для самостоятельной работы со студентами по данному модулю календарного плана.
На втором этапе составляется матричный и сетевой планы. Матричный план – это таблица, содержащая тот материал календарного плана, что должен выполнить каждый студент самостоятельно в течение модуля. Задания также записываются с помощью символов, которые впоследствии будут представлены в графической модели. В сетевой план переносятся все виды работы, содержащиеся в матричном плане, уже обозначенные символами, последовательность выполнения заданий указывается стрелками [6].
На третьем этапе проводится конкретизация материала, отбираются задания для каждого вида самостоятельной работы, содержащейся в матричном и сетевом плане. Например, при формировании блока задач по модулю «Производная функции одной переменной» были отобраны следующие задания [7-9].
I. Задачи, направленные на закрепление фундаментальных понятий математического анализа – производной и дифференциала функции, на умение применять основные теоремы о дифференцируемых функциях:
1. Применяя определение производной функции, вывести формулу для вычисления производной функции 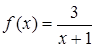 в точке
в точке 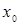 .
.
2. Исследуйте функцию 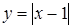 на непрерывность и дифференцируемость в точке
на непрерывность и дифференцируемость в точке 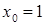 .
.
3. Докажите, что производная четной дифференцируемой функции есть нечетная функция.
4. Написать формулу Лагранжа и найти с для функции 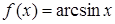 на отрезке
на отрезке 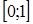 .
.
5. Применима ли теорема Ролля к функции 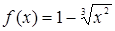 на отрезке
на отрезке 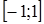 ? Пояснить графически.
? Пояснить графически.
II. Задачи, направленные на закрепление навыков техники дифференцирования с помощью таблицы производных, умения применять правила дифференцирования, умения преобразовывать алгебраические и тригонометрические выражения:
6. Найти 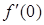 , если
, если 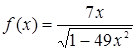 .
.
7. Вычислить производную функций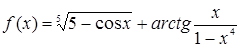 .
.
8. Докажите, что функция 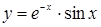 удовлетворяет уравнению
удовлетворяет уравнению 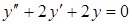 .
.
9. Найти первую и вторую производную функции, заданной параметрически 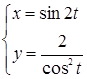 при
при 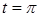 .
.
10. Пользуясь правилом Лопиталя, вычислить предел 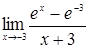 .
.
III. Задачи, при решении которых используются знания ранее изученных математических дисциплин, задачи на геометрическое и физическое приложения производной, задачи на использование дифференциала в приближенных вычислениях:
11. Найти 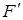 , если
, если 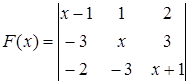 .
.
12. Составьте уравнения касательной и нормали, проведенных к графику функции 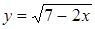 в точке
в точке 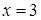 .
.
13. При каком значении переменной x касательные к графикам функций  и
и 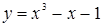 параллельны между собой?
параллельны между собой?
14. Тело движется прямолинейно в вертикальном направлении по закону 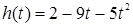 . Определите начальную скорость и начальное положение тела по отношению к земле. Приземлится ли тело? Если да, то через сколько секунд после начала движения? Определите скорость тела в момент приземления.
. Определите начальную скорость и начальное положение тела по отношению к земле. Приземлится ли тело? Если да, то через сколько секунд после начала движения? Определите скорость тела в момент приземления.
15. Многогранник составлен из двух прямых призм с квадратным и треугольным основанием. Основанием многогранника служит боковая грань четырехугольной призмы. При каких значениях длины стороны квадрата объем данного многогранника увеличивается, а при каких – уменьшается, если периметр основания многогранника остается постоянным, равным 24?
Автором статьи на основе сформулированных принципов разработана методика обучения математике для бакалавров технического вуза, эффективность которой была подтверждена в ходе проведения педагогического эксперимента [6]. На рисунке показана связь компонентов методики и влияние на них изложенных принципов.
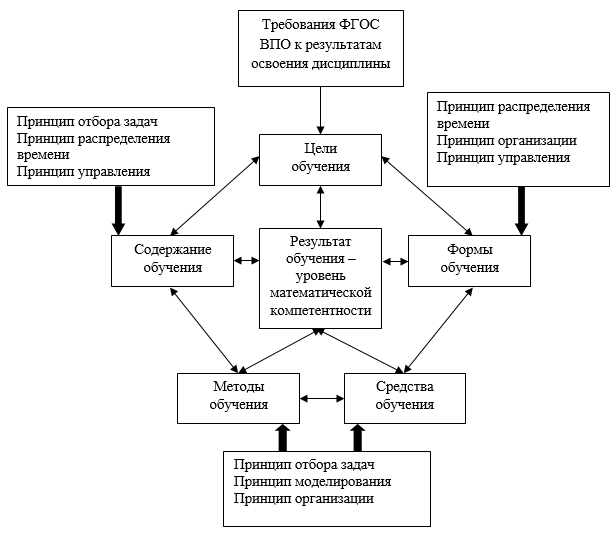
Модель методики, направленной на повышение математической компетентности бакалавров
Библиографическая ссылка
Анисова Т.Л. ПРИНЦИПЫ МЕТОДИКИ ОБУЧЕНИЯ МАТЕМАТИКЕ, НАПРАВЛЕННОЙ НА ПОВЫШЕНИЕ МАТЕМАТИЧЕСКОЙ КОМПЕТЕНТНОСТИ БАКАЛАВРОВ // Современные проблемы науки и образования. 2018. № 1. ;URL: https://science-education.ru/ru/article/view?id=27326 (дата обращения: 05.02.2026).