Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Лопатина Н.В. 1 Мишанькин Б.Н. 2 Аветисян З.Е. 1

---

1 ФГБОУ ВО «Ростовский государственный медицинский университет» Минздрава России

2 ФКУЗ «Ростовский-на-Дону противочумный институт» Роспотребнадзора

Целью исследования является оценка показателей термостабильности вакцины EV, прогнозированных с помощью двух вариантов теста «ускоренного старения», в сравнении с результатами прямого эксперимента. Для определения констант скоростей термоинактивации и показателей термостабильности вакцины EV использовали уравнение Вант-Гоффа (экспресс-метод) и метод Аррениуса с построением графика. В прямом эксперименте (путем высева на питательные среды) определяли количество оставшихся в живых клеток Y. pestis EV в вакцине, хранившейся в условиях низкой температуры +4 °С, и сравнивали с прогнозированными данными, рассчитанными по методам Вант-Гоффа и Аррениуса. Показано, что расчетные по методу Аррениуса показатели были более достоверными, чем полученные с использованием метода Вант-Гоффа, и практически совпадали с результатами прямого эксперимента. На основе реализации метода Аррениуса разработан экспресс-вариант метода Аррениуса с использованием трех высокотемпературных точек, позволяющий в кратчайшие сроки получить наиболее достоверный прогноз сроков годности живой сухой чумной вакцины. Предложены новые подходы к определению сроков годности вакцины перед использованием её в практике здравоохранения.

Статья в формате PDF

204 KB

прямой эксперимент

прогноз

график

уравнение аррениуса

правило вант-гоффа

термостабильность

1. Аттестация и продление срока годности новой серии отраслевого стандартного образца специфической активности и иммуногенности вакцины туляремийной живой / И.В. Касина [и др.] // Биопрепараты. Профилактика. Диагностика. Лечение. – 2015. – № 4 (56). – С. 32-38.

2. Изучение стабильности антигенных компонентов чумной химической вакцины (Ф1+ОСА) в тестах на «ускоренное старение» и стресс-условия / М.Н. Киреев [и др.] // Проблемы ООИ. – 2009. – 99. – С. 70-74.

3. Кенжебаева М.К. Получение термостабильного варианта вируса Ньюкаслской болезни и изучение его иммунобиологических свойств / М.К. Кенжебаева, М.Б. Матроимов, М. Мамбеталиев // Наука, новые технологии и инновации. – 2016. – № 3. – С. 77.

4. Лопатина Н.В. Изучение термостабильности экспериментальных образцов живой сухой чумной вакцины, приготовленных на основе референтного, селекционированного и генетически измененных вариантов штамма Yersinia Pestis EV с использованием питательных сред / Н.В. Лопатина, З.Е. Аветисян // Сборники конференций НИЦ Социосфера. – 2016. – № 56. – С. 102-108.

5. Печникова И.В., Тинкер А.И. Методика определения термостабильности живых сухих чумных вакцин и прогнозирования их жизнеспособности в процессе хранения: методические рекомендации. – Ставрополь, 1985. – 11 с.

6. Разработка и изучение отраслевого стандартного образца активности вакцины против краснухи / Т.Н. Юнасова [и др.] // Биопрепараты. Профилактика. Диагностика. Лечение. – 2015. – № 3 (55). – С. 49-53.

7. Результаты переаттестации отраслевого стандартного образца активности, специфичности и некротической активности оспенной вакцины / А.В. Мухачева [и др.] // Биопрепараты. Профилактика. Диагностика. Лечение. – 2013. – № 4 (48). – С. 34-41.

8. Сравнительный анализ экспериментальных серий вакцины чумной живой сухой по показателям жизнеспособности и термостабильности / Д.А. Будыка [и др.] // Проблемы ООИ. – 2009. – № 4 (102). – С. 68-71.

9. Svante Arrhenius [Электронный ресурс]. - Режим доступа: https://en.wikipedia.org/wiki/Svante_Arrhenius (дата обращения: 06.07.2017).

Основными составляющими, характеризующими качество вакцин, являются: иммуногенность, безопасность и стабильность. Для оценки термостабильности лиофилизированных форм препаратов применяется известный методический прием-тест «ускоренного старения» [5].

Эффективность этого теста, применительно к биологическим агентам, зависит от многих факторов: природы реагирующих веществ, их концентрации, рН реакционной среды, физического состояния, температуры, состава питательных и защитных сред, схем лиофилизации ингибиторов или стимуляторов [1-4; 7; 8].

Цель исследования состояла в сравнительной оценке показателей термостабильности вакцины EV, прогнозированных при реализации двух вариантов теста «ускоренного старения», с результатами прямого эксперимента.

Материал и методы исследования

В опытах использовано 3 серии чумной вакцины EV. Препараты готовили на лиофилизационной установке фирмы Фригера LZ-9CP (ЧСФ) с использованием питательной среды «СО» и защитной сахарозо-желатиновой среды с тиомочевиной по заранее разработанной схеме лиофилизации [4]. Показатели термостабильности, характеризующие время 50% снижения количества клеток в вакцине при хранении её в низкотемпературных условиях (+ 4 °С), были определены экспресс-вариантом теста «ускоренного старения» (правило Вант-Гоффа) [5] и графическим методом Сванте Аррениуса [9].

Методика проведения эксперимента в соответствии с правилом Вант-Гоффа состоит в выдерживании образцов вакцины в трех высокотемпературных режимах: при температуре 37 °С, экспозиции 14 суток; 47 °С, экспозиции 4 суток; 57 °С, экспозиции 2 суток. После сохранения препаратов в каждом режиме содержимое ампул титровали в физиологическом растворе до 100 и 1000 клеток, высевали на питательную среду «СО» и подсчитывали количество КОЕ (колониеобразующих единиц). Константы скоростей термоинактивации определяли по формуле [5]:

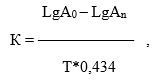
где LgA0 - логарифм числа живых микробных клеток после лиофилизации; LgAn – логарифм живых микробных клеток после выдерживания вакцинных препаратов в разных температурных условиях, в сутках; Т – температура; 0,434 – модуль перехода от натуральных логарифмов к десятичным. Для определения показателя термостабильности препарата использовали формулу

Константу скорости отмирания микробных клеток при +4 °С определяли по цифровой модели Вант-Гоффа.

Метод оценки стабильности препарата по Аррениусу основан на двух теоретических положениях [6; 9]:

1. Тепловая инактивация биообъекта может быть описана кинетическим уравнением первого порядка lgY = lgY0 - К×t, где Y0 – исходная активность биообъекта; Y – величина активности через время t; К – константа скорости инактивации (1/ ед. времени). В координатах lg У от t данное уравнение – прямая линия с тангенсом угла наклона к оси Х, равным константе скорости инактивации.

2. Константа скорости инактивации зависит не только от температуры, но и от ве­личины энергии активации, т.е. энергетического барьера, который должны преодолеть молекулы вещества для осуществления реакции. Это положение впервые было установлено Сванте Аррениусом, который ввел эту величину в разработанное им уравнение: K = Аe-Ea/RT или lnk = Ea/RT + lnA, где Кт – константа скорости инактивации (1/ ед. времени); T – абсолютная температура (°К); R= 1,987 кал/град×моль (газовая постоянная Больцмана); Ea – эмпирическая энергия активации (кал/моль); А - предэкспоненциальный множитель. Константы скоростей термоинактивации для прогноза сроков годности исследуемых серий вакцины определяли по графику Аррениуса с предварительным расчетом величины энергии активации. В аррениусовских координатах InКТ от 1/Т данное уравнение изображается прямой линией, тангенс угла наклона которой отражает энергию активации. С помощью этого графика методом экстраполяции определяли величину Кт при температуре +4 °С и рассчитывали сроки годности вакцины. Для построения графика выбрано 6 высокотемпературных точек, в которые помещали препараты вакцины: (27, 37, 47, 57, 67, 77 °С). Время наблюдения за снижением количества клеток зависело от температуры хранения и составляло от 6 часов до 1,5 месяцев.

При реализации прямого эксперимента ампулы вакцины, хранящиеся 100 суток при температуре +4 °С, вскрывали, содержимое титровали в физиологическом растворе, высевали 100 и 1000 клеток на питательную среду «СО» и проводили подсчет КОЕ (колониеобразующих единиц).

Константы скоростей отмирания микробных клеток и показатели термостабильности, полученные с применением каждого из методов, сравнивали между собой и данными прямого эксперимента.

Для статистической обработки величин констант скоростей термоинактивации в работе использовали метод наименьших квадратов, который заключается в минимизации суммы квадратов отклонений и предусматривает выбор вектора, минимизирующего ошибку.

Результаты и обсуждение

Константы скоростей термоинактивации микробных клеток, прогнозированные для каждой температуры (6 температурных точек) по графику Аррениуса, были более высокими, чем соответствующие показатели, рассчитанные по правилу Вант-Гоффа (табл. 1, 2, график Аррениуса).

Таблица 1

Значение констант скоростей термоинактивации клеток в вакцине в процессе хранения при повышенных температурах

График Аррениуса для определения констант скоростей термоинактивации экспериментальных серий вакцины EV

Метод Аррениуса предусматривает постановку опыта по хранению вакцины в разных температурных режимах с использованием большого количества высокотемпературных точек, что обеспечивает высокую точность прогноза исследуемых величин, но увеличивает время получения результата до 1,5 месяцев. Поэтому целесообразно было исследовать на графике Аррениуса комбинации различных сочетаний повышенных температур и выбрать оптимальные значения трех температур для получения достоверного прогноза в более сокращенные сроки (табл. 2).

Таблица 2

Прогнозированные константы скоростей термоинактивации микробных клеток и прогноз сроков хранения вакцин по методу и графику Аррениуса

В таблице 2 показано, что диапазон и значение высокотемпературных точек, взятых в опыт, оказывают существенное влияние на объективность прогноза. Из 17 исследованных комбинаций точек полное совпадение прогнозированных показателей термостабильности с результатами основного эксперимента (по 6 точкам) наблюдалось с использованием в опыте 3 точек: 47, 57, 67 °С.

О преимуществе метода Аррениуса свидетельствует расчетное количество оставшихся в живых клеток через 100 суток хранения при +4 °С, в наибольшей степени совпадающее с результатами прямого эксперимента, в то время как прогноз по правилу Вант-Гоффа был менее точным. В опытах прямого эксперимента при высеве на питательную среду 100 клеток из ампул вакцины, хранившихся при температуре +4 °С, количество живых клеток снизилось с 25,5±2,4 до 18,9± 1,9, в то время как соответствующие прогнозированные показатели, рассчитанные по методу Вант-Гоффа, составили – 25±2,3, а по методу Аррениуса – 19,8± 2,1.

С учетом оценки результатов прямых методов расчетные показатели термостабильности по Вант-Гоффу оказались намного выше реальных – 1470 суток, против – 987 по Аррениусу.

Таким образом, в лабораторных условиях было показано, что уравнение Аррениуса более точно и универсально выражает зависимость константы скорости реакции от температуры, что позволило рассчитать количество клеток через 100 суток хранения, наиболее приближенное к реальному.

Путем исследования в эксперименте большого количества высокотемпературных точек и их сочетаний для разработки экспресс-метода Аррениуса выявлены оптимальные сочетания температур (47, 57, 67 °С). Использование этих точек в опыте позволяет в режиме экспресс-прогноза за 4-5 суток не только с большой точностью прогнозировать сроки годности вакцины, но и значительно уменьшить сроки проведения опыта: в 9-10 раз по сравнению с использованием 6 точек по Аррениусу и в 3,5 раза – по сравнению с экспресс-методом Вант-Гоффа.

Однако выявленные расхождения в точности прогноза не исключают применение правила Вант-Гоффа при экспериментальном изучении вклада каждого этапа биотехнологии в общий технологический процесс получения вакцины, но в случае выпуска серии вакцины в практику здравоохранения прогноз должен быть максимально достоверным. Как было показано в эксперименте, наиболее корректно температурную зависимость скорости реакции термоинактивации описывает уравнение Аррениуса. Учитывая вариабельность показателей термостабильности от вида и штамма микроорганизма, среды культивирования и даже серии питательной среды [8], необходимо применять аррениусовский способ прогнозирования констант скоростей термоинактивации и, следовательно, показателей термостабильности с построением графика Аррениуса для каждой выпускаемой серии вакцины, не ограничивая прогноз использованием одной повышенной температуры [5].

Это обстоятельство диктует новые подходы к определению сроков годности вакцины перед применением её в практике здравоохранения в плане предварительной корректировки метода оценки термостабильности для коммерческих серий препарата. Поэтому используемые в настоящее время методики для проведения теста «ускоренного старения», основанные на общепризнанных теоретических положениях, требуют конкретизации с учетом особенностей биологических объектов и их назначения.

Библиографическая ссылка