В современном мире финансово грамотное население является одним из значимых факторов хорошей экономической ситуации в любой стране. Умение большинства членов общества ставить финансовые цели, самостоятельно обеспечивать свой жизненный цикл ведет к повышению их уровня жизни, появлению уверенности в завтрашнем дне и, соответственно, к стабильности общества и развитию экономики всей страны.
Однако, как показало одно из последних исследований по изучению финансового поведения населения в России, проведенное исследовательским центром «Демоскоп» в рамках совместного проекта Министерства финансов России и Всемирного банка (6103 домохозяйства, 12650 человек из 158 городов и сельских населённых пунктов в 32 российских регионах), результаты неутешительны. Большая часть россиян живет «от зарплаты до зарплаты», планируя в основном лишь на месяц вперед. О планах на более долгий срок, например, на год и более, задумываются всего 9 % россиян. В качестве дополнительного источника доходов россияне используют кредиты, непогашенная задолженность по которым имеется у 31,9 % респондентов. Кредитные карты имеются у почти 20 % домохозяйств. И лишь 45,1 % российских семей осознанно создают «финансовую подушку безопасности», откладывая на «черный день» [1].
На сегодняшний день в России уделяется значительное внимание решению проблемы повышения уровня финансовой грамотности всех категорий населения. На государственном уровне принят ряд нормативных документов, регламентирующих ее решение, таких как «Стратегия развития финансового рынка РФ на период до 2020 года» [2], «Концепция долгосрочного социально-экономического развития РФ на период до 2020 года» [3] и др. В их русле с 2011 года реализуется Совместный проект Минфина России и Всемирного банка «Содействие повышению уровня финансовой грамотности населения и развитию финансового образования в РФ» [4].
САФУ является непосредственным участником данного проекта в качестве соисполнителя региональной программы «Повышение уровня финансовой грамотности населения и развитие финансового образования в Архангельской области в 2014–2019 годах». Основная его цель – повышение уровня финансовой грамотности обучающихся САФУ.
Общими для всех регионов, участвующих в реализации проекта, являются ежегодные Всероссийская неделя сбережений и Всероссийская неделя финансовой грамотности для детей и молодежи. В САФУ в их рамках проводятся лекции, семинары, мастер-классы, образовательные компьютерные, интеллектуальные и деловые игры и др. С 2016 года эти ежегодные мероприятия пополнились еще одним. 29 октября в нескольких странах (Болгария, Казахстан, Россия, Туркменистан) прошла первая Международная олимпиада по финансовой и актуарной математике [5].
Учредителями олимпиады являются Экономический университет – Варна (Варна, Болгария) и Высшая школа финансов, бизнеса и страхования (София, Болгария). Организаторы от Болгарии: Экономический университет – Варна (Варна); Высшая школа финансов, бизнеса и страхования (София); от России: ФГАОУ ВО «Северный (Арктический) федеральный университет имени М.В. Ломоносова (Архангельск); ФГАОУ ВО «Уральский федеральный университет имени Б. Ельцина» (Екатеринбург); ФГБОУ ВО МО «Академия социального управления» (Москва); ФГБОУ ВО «Елецкий государственный университет им. И.А. Бунина»; АНО ВО «Московский региональный социально-экономический институт» (Московская область г. Видное); от Туркменистана: Международный университет гуманитарных наук и развития (Ашхабад); от Казахстана: Республиканский научно-практический центр «Дарын» и др.
Согласно положению об олимпиаде, ее основными целями и задачами являются:
- мотивация различных категорий населения к повышению своей финансовой грамотности;
- привлечение внимания к важности использования математических средств и методов при принятии разумных финансовых решений, как в профессиональных, так и бытовых ситуациях;
- отбор среди участников олимпиады кандидатов в тьюторы по повышению финансовой грамотности населения для последующего их рекрутинга на программы специальной подготовки;
- развитие международного сотрудничества в целях наиболее эффективного решения задач повышения финансовой грамотности населения.
Первая часть олимпиады предназначалась для возрастной категории студенты и взрослые. В САФУ олимпиада проходила на трех площадках: высшая школа информационных технологий и автоматизированных систем (ВШИТАС); высшая школа экономики, управления и права (ВШЭУП), гуманитарный институт филиала САФУ в городе Северодвинске (ГИ). Всего в олимпиаде приняло участие 172 человека.
Студенты за 120 минут должны были решить семь задач, пять – в тестовой форме, одна – с кратким ответом, одна – с полным решением. Темами заданий предполагались «… все актуальные вопросы оперирования финансами: динамика цен и инфляция, кредиты и условия их досрочного погашения, движение средств на зарплатном счете, инвестиции, страхование, срочные депозиты, динамика процентных ставок, оперирование вложениями» [6, С. 3].
Первые пять задач представлялись в тестовой форме. За правильный ответ можно было получить три балла. Представим эти задачи, их возможное решение и анализ необходимого экономического и математического аппарата, необходимого для решения.
Задание 1. Цена данного товара снизилась в сентябре на 17 % по сравнению с августом и на 6 % в октябре по сравнению с сентябрем. Определите процент снижения цены товара в октябре по сравнению с августом.
А) 23 % В) 11 % С) 102 % D) 20,23 % E) 21,98 %
Решение 1 (авторское). Пусть цена товара в августе 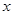 . Тогда ее цена в сентябре равна
. Тогда ее цена в сентябре равна 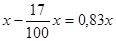 ,
,
a в октябре: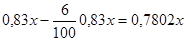 . Изменение цены в октябре по сравнению с августом равно
. Изменение цены в октябре по сравнению с августом равно
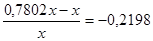 , то есть цена снизилась на 21,98 %.
, то есть цена снизилась на 21,98 %.
Ответ: E
Представим в табличной форме математический и экономический аппарат, необходимые для решения задач, а также возраст владения всеми этими знаниями (табл. 1–9).
Таблица 1
Экономический и математический аппарат, необходимый для решения задачи 1 авторским способом
|
Экономический аппарат |
Курс экономики |
Математический аппарат |
Курс математики |
|
понятие и формула процентного изменения |
углубленный курс экономики в школе/вуз |
простые и десятичные дроби, уравнения с одной переменной, простые проценты |
6 класс |
Решение 2 (наше)
Пусть цена товара в августе 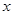 . Тогда ее цена в сентябре равна
. Тогда ее цена в сентябре равна 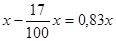 ,
,
a в октябре: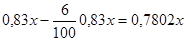 .
.
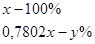
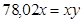
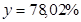
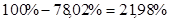
Ответ: E.
Таблица 2
Экономический и математический аппарат, необходимый для решения задачи 1 нашим способом
|
Экономический аппарат |
Курс экономики |
Математический аппарат |
Курс математики |
|
не требуется |
- |
простые и десятичные дроби, уравнения с двумя переменными, простые проценты |
8 класс |
Таким образом, данную задачу должны были решить как студенты экономических, так и математических специальностей, даже при невладении ими соответствующим экономическим понятием.
Задание 2. Определите индекс инфляции в 2015 г. по сравнению с 2014 г., если известны цены и потребление 10 видов товаров:
|
Товар |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Потребление 2014 г. |
60 |
240 |
100 |
120 |
300 |
40 |
160 |
800 |
210 |
420 |
|
Цена 2014 г. |
6 |
0,9 |
4,5 |
8 |
3,5 |
12 |
2,1 |
0,5 |
8 |
4,2 |
|
Цена 2015 г. |
6,2 |
1,1 |
4,3 |
7 |
4 |
15 |
2 |
0,8 |
9 |
5 |
А) 0,89 В) 1,12 С) 1,12 % D) 12,47 % E) 1,5
Решение (авторское). Пусть 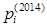 ,
, 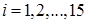 – цены товаров в 2014 г.,
– цены товаров в 2014 г., 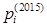 ,
, 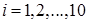 – цены товаров в 2015 г., а
– цены товаров в 2015 г., а 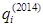 ,
, 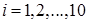 – потребленные количества товаров в 2014 г. Индекс инфляции равен
– потребленные количества товаров в 2014 г. Индекс инфляции равен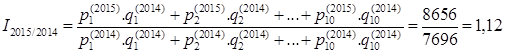 .
.
Ответ: В
Таблица 3
Экономический и математический аппарат, необходимый для решения задачи 2 авторским способом
|
Экономический аппарат |
Курс экономики |
Математический аппарат |
Курс математики |
|
понятия «инфляция», «индекс инфляции», формула нахождения индекса инфляции (формула Ласпейреса) |
10-11 класс |
основные арифметические действия с натуральными числами и десятичными дробями. |
5 класс |
Таким образом, для решения этой задачи было достаточно школьных знаний, как экономики, так и математики.
Задание 3. Найдите максимальную сумму (до второго знака после запятой), которую инвестор готов вкладывать в проект, если этот проект генерирует будущие доходы, соответственно 10000 евро в первом году и 200000 евро во втором году и инвестора удовлетворяет доходность 6,25%.
А) 201251,4 В) 152387,26 С) 12250 D) 186574,39 E) 190258,18.
Решение (авторское):
Инвестиция является приемлемой, если чистая приведённая стоимость 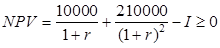 , где r – желаемый уровень доходности, I – размер инвестиции. Ищем максимальное значение I0, для которого выполнено
, где r – желаемый уровень доходности, I – размер инвестиции. Ищем максимальное значение I0, для которого выполнено 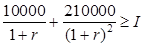 для
для 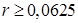 . Функция
. Функция 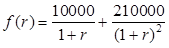 монотонно убывающая для каждого
монотонно убывающая для каждого 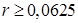 (так как
(так как 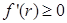 для каждого
для каждого 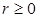 ). Тогда
). Тогда 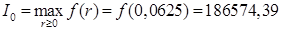 .
.
Ответ: D
Таблица 4
Экономический и математический аппарат, необходимый для решения задачи 3 авторским способом
|
Экономический аппарат |
Курс экономики |
Математический аппарат |
Курс математики |
|
понятия инвестиция, приемлемая инвестиция, чистая приведенная стоимость, доходность (инвестиций), размер инвестиции; формула чистой приведенной стоимости |
10-11 класс с углубленным изучением экономики/ вуз |
функция, производная, монотонность функции, критерий монотонности функции, максимальное значение функции. |
10 класс с углубленным изучением математики/ вуз (курс математического анализа) |
Таким образом, для решения этой задачи были необходимы как углубленные/вузовские знания экономики, так и углубленные/вузовские знания математики.
Задание 4. Пусть сумма 10000 евро кладется на срочный одномесячный депозит при р % сложной ставке. В конце первого месяца к накопленной сумме добавляются 5000 евро и они кладутся на тот же самый депозит. В конце второго месяца к накопленной сумме добавляются 2500 евро и они также кладутся на тот же самый депозит. Какой минимальный процент р гарантирует, что в конце третьего месяца накопленная сумма будет не менее 20000 евро.
А) 2% В) 3% С) 4% D) 5% E) 6%
Решение (авторское).
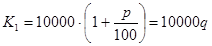 ,
,
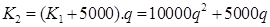 ,
,
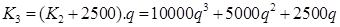 .
.
Необходимо, что 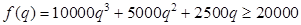
Если 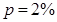 , то
, то 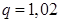 и
и 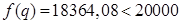 .
.
Если 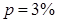 , то
, то 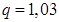 и
и 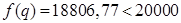 .
.
Если 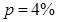 , то
, то 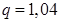 и
и 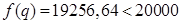 .
.
Если 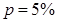 , то
, то 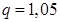 и
и 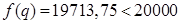 .
.
Если 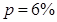 , то
, то 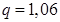 и
и 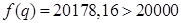 .
.
Ответ: Е
Таблица 5
Экономический и математический аппарат, необходимый для решения задачи 4 авторским способом
|
Экономический аппарат |
Курс экономики |
Математический аппарат |
Курс математики |
|
понятие депозит, формула увеличения числа на заданный процент |
дополнительное образование, вуз |
сложные проценты, возведение в степень, функция, формула увеличения числа на заданный процент |
9 класс |
Решение (наше, при незнании формулы увеличения числа на заданный процент).
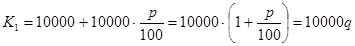
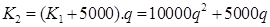 ,
,
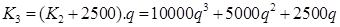 .
.
Необходимо, что 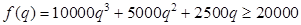
Если 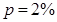 , то
, то 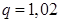 и
и 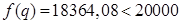 .
.
Если 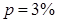 , то
, то 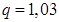 и
и 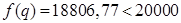 .
.
Если 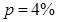 , то
, то 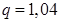 и
и 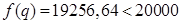 .
.
Если 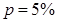 , то
, то 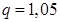 и
и 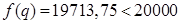 .
.
Если 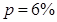 , то
, то 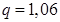 и
и 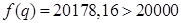 .
.
Ответ: Е
Таблица 6
Экономический и математический аппарат, необходимый для решения задачи 4 нашим способом
|
Экономический аппарат |
Курс экономики |
Математический аппарат |
Курс математики |
|
понятие депозит |
дополнительное образование, вуз |
сложные проценты, возведение в степень, функция |
9 класс |
Таким образом, для решения задачи достаточно понимания термина «депозит» и владения математическими знаниями в рамках 9 класса.
Задание 5. Сумма в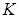 евро была положена в банк при сложной ставке
евро была положена в банк при сложной ставке 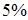 . В конце каждого года
. В конце каждого года 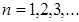 выплачивают 1000 евро. Найти минимальную сумму К, чтобы процесс был бесконечным.
выплачивают 1000 евро. Найти минимальную сумму К, чтобы процесс был бесконечным.
А) 100000 евро В) 10000 евро С) 1500 евро D) 20000 евро E) 50000 евро
Решение (авторское). Начальная сумма К должна быть не менее чем текущей стоимости всех будущих доходов (до бесконечности) при дисконтной ставке 5%:
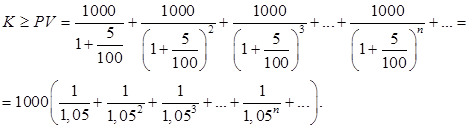
Так как 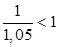 , то
, то 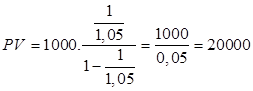 . Следовательно
. Следовательно 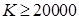 и
и 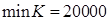 евро.
евро.
Ответ: D
Таблица 7
Экономический и математический аппарат, необходимый для решения задачи 5 авторским способом
|
Экономический аппарат |
Курс экономики |
Математический аппарат |
Курс математики |
|
дисконтная ставка, сложная и простая ставка, текущая стоимость, доход, формула расчета текущей стоимости (формула дисконтирования) |
вуз (экономическое образование) |
возведение в степень, минимальное значение, бесконечно убывающая геометрическая прогрессия, формула суммы бесконечно убывающей геометрической прогрессии, ряды, бесконечно убывающий ряд, частичная сумма ряда, предел частичной суммы ряда |
вуз (математическое образование) |
Таким образом, пятая задача требовала знаний как в области экономики, так и в области математики в рамках вузовского курса соответствующих направлений обучения.
Представим на диаграмме соотношение выполнивших тестовые задания 1–5 студентов, представленных выше подразделений САФУ (диаграмма 1).
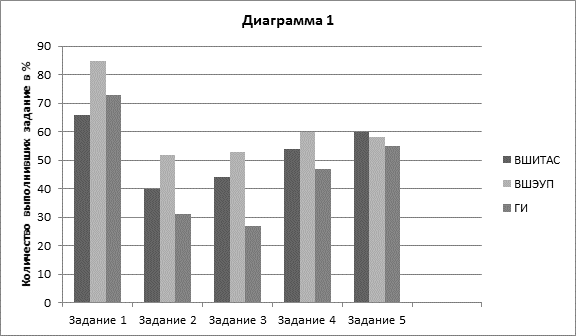
Выводы по заданиям 1-5 (в тестовой форме). Лучше всего студенты всех подразделений справились с заданием 1, требующим либо знание формулы процентного изменения, либо умения составить и решить уравнение с двумя переменными. Как видно на диаграмме, знающие формулу студенты-экономисты и менеджеры решили задачу лучше, чем математики.
Хуже всего студентам всех подразделений дались задание 2, построенное на материале школьного курса экономики 10-11 класса и математическом аппарате, доступном пятиклассникам, что вызывает некоторое удивление; а также задание 3, требующее владения как понятиями и формулами экономики, так и математики на уровне углубленного изучения обоих предметов или вуза. Очевидно, большинство студентов не помнят со школы понятие индекса инфляции и формулу его вычисления (задание 2), а также недостаточно хорошо владеют понятиями приемлемая инвестиция, чистая приведенная стоимость, доходность инвестиций, размер инвестиции, формула чистой приведенной стоимости (задание 3).
Немного лучше все студенты справились с заданием 4, требующем знания понятия «депозит» и математики на уровне 9 класса (стоит отметить, что подобные задачи часто встречаются на ЕГЭ по математике и должны быть знакомы студентам начальных курсов) и с заданием 5, требующем либо знания формулы дисконтирования, либо знания вузовской математики по теме «ряды».
Выполнение задания 6 требовало получения ответа и его записи без приведения решения (задание с кратким ответом). За его решение можно было получить 5 баллов.
Задание 6. Инвестор имеет возможность инвестировать 100000 евро в двух типов активов – А и В. Ожидаемые годовые доходности соответственно 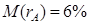 и
и 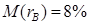 , а среднеквадратические отклонения от ожидаемых доходностей соответственно
, а среднеквадратические отклонения от ожидаемых доходностей соответственно 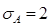 и
и 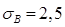 . Коэффициент корреляции
. Коэффициент корреляции 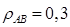 . Какую сумму должен инвестор вкладывать в А и В, чтобы общая дисперсия доходности (
. Какую сумму должен инвестор вкладывать в А и В, чтобы общая дисперсия доходности (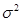 ) была минимальной?
) была минимальной?
Решение (авторское). Пусть инвестированный капитал равен 1, х – часть, инвестирована в А и (1-х) – часть, инвестирована в В, 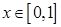 . Портфель из двух активов р имеет характеристики:
. Портфель из двух активов р имеет характеристики:
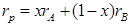 (доходность портфеля);
(доходность портфеля);
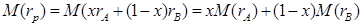 (ожидаемая доходность портфеля), которое следует из свойств математического ожидания. Согласно определению дисперсии:
(ожидаемая доходность портфеля), которое следует из свойств математического ожидания. Согласно определению дисперсии:
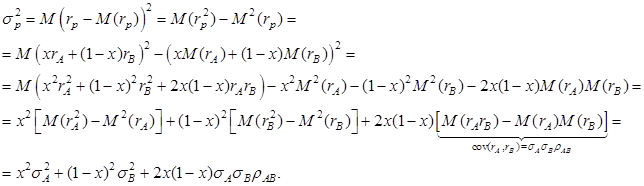
То есть
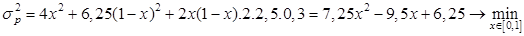 .
.
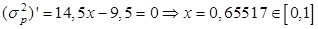 и
и 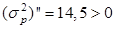 , следовательно
, следовательно 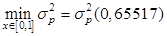 .
.
Инвестор должен вкладывать 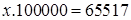 евро в А и
евро в А и 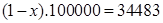 евро в В.
евро в В.
Ответ: 65517 евро в А и 34483 евро в В.
Таблица 8
Экономический и математический аппарат, необходимый для решения задачи 6 авторским способом
|
Экономический аппарат |
Курс экономики |
Математический аппарат |
Курс математики |
|
портфель, доходность портфеля, формула доходности портфеля, формула ожидаемой доходности портфеля |
вуз (экономические специальности) |
возведение в степень, производная, минимальное значение функции, среднеквадратическое отклонение, дисперсия, математическое ожидание, коэффициент корреляции, коэффициент ковариации: понятия и формулы. |
вуз (после прохождения курса теории вероятностей и математической статистики) |
Таким образом, решение задачи требует знаний как экономических понятий, так и математики на уровне вузовских курсов. Причем, курс теории вероятностей и математической статистики изучается на всех направлениях обучения, экономические же понятия и формулы, необходимые для решения задачи, изучаются только студентами экономических направлений обучения. Для студентов-математиков, в отличие от всех остальных задач, имеющих возможность вывести незнакомые из курса экономики формулы опираясь на математические знания, эта задача была изначально нерешима.
Диаграмма 2 демонстрирует выполнение задания 6.
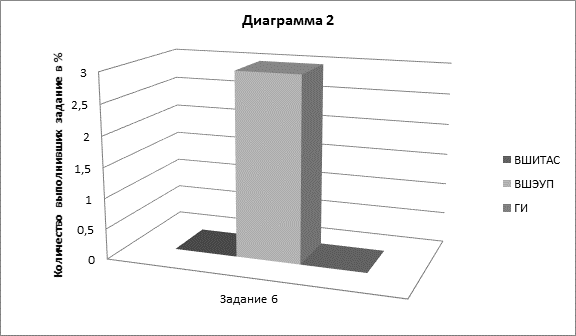
Вывод по заданию 6 (с кратким ответом)
Очевидно, это задание оказалось практически непосильным для студентов всех подразделений. С ним справились только два человека, обучающихся на экономическом направлении, что составляет 1 % всех писавших олимпиаду студентов.
Выполнение задания 7 требовало записи полного решения. В зависимости от полноты решения студент мог заработать за него от 3 до 10 баллов в соответствии со следующими критериями: 10 баллов – обоснованно получен верный ответ, 8 баллов – полученное уравнение представлено в виде суммы двух полных квадратов, но получен неверный ответ из-за вычислительной ошибки, 6 баллов – если выделен квадрат только одного из выражений, входящих в полученное уравнение, 3 балла – если составлено уравнение, но оно не решено, 0 баллов – во всех остальных случаях.
Задание 7. Известны функциональные зависимости ежемесячной прибыли 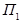 и
и 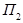 двух конкурирующих компаний в зависимости от значений трех факторов
двух конкурирующих компаний в зависимости от значений трех факторов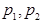 и
и 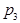 :
:
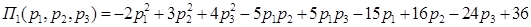 ;
;
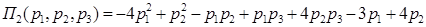 .
.
Если 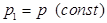 и
и 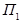 =
=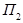 , то
, то 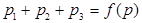 = ?
= ?
Решение: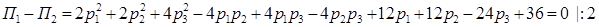 ,
,
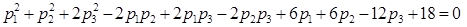 ,
,
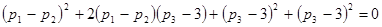
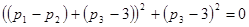
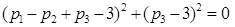
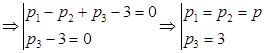 .
.
Тогда 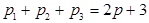 .
.
Ответ: 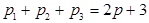
Таблица 9
Экономический и математический аппарат, необходимый для решения задачи 7 авторским способом
|
Экономический аппарат |
Курс экономики |
Математический аппарат |
Курс математики |
|
не требуется |
- |
возведение в степень, функциональная зависимость, формулы сокращенного умножения |
7 класс |
Таким образом, для решения этой задачи достаточно было знания материала 7 класса школьного курса математики.
На диаграмме 3 представлены баллы, заработанные студентами разных подразделений за решение этой задачи.
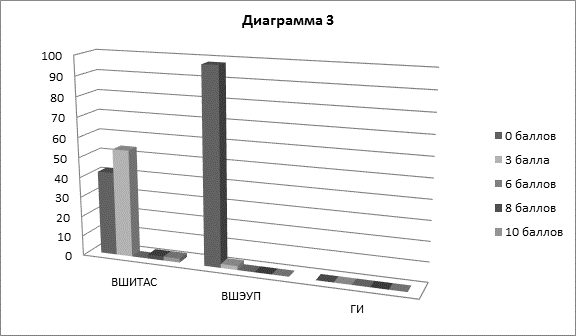
В результате только один студент ВШИТАС решил задачу полностью, еще один составил верные выражения, но допустил в решении вычислительную ошибку, и чуть более половины студентов ВШИТАС и два студента ВШЭУП справились с составлением уравнения, но задачу не решили. Как видно из диаграммы 3, лучше всего результаты по решению чисто математической задачи, как и следовало ожидать, у студентов-математиков.
Приведем несколько комментариев студентов относительно заданий олимпиады: «Олимпиада была сложная, но интересная. После нее появилась мотивация к повышению финансовой грамотности», «Над заданиями олимпиады действительно пришлось подумать. Некоторые из них показались мне очень сложными, и мне не хватило знаний решить их» [5].
Таким образом, на наш взгляд, составителям заданий олимпиады в следующем году следует обратить внимание на то, что составление задач требует соблюдения равных условий как для студентов-экономистов, так и для студентов-математиков, то есть они должны строиться на материале экономики, дающем возможность выведения соответствующих формул студентам неэкономических направлений обучения или на материале школьного курса экономики. С математической точки зрения все задачи были равноправными, так как имели возможность решения либо с применением материала школьного курса математики, либо изучающегося всеми направлениями обучения студентами.
Библиографическая ссылка
Форкунова Л.В., Лукина В.С., Милкова Т.В. ПЕРВАЯ МЕЖДУНАРОДНАЯ ОЛИМПИАДА ПО ФИНАНСОВОЙ И АКТУАРНОЙ МАТЕМАТИКЕ: РЕЗУЛЬТАТЫ ПО АРХАНГЕЛЬСКОЙ ОБЛАСТИ // Современные проблемы науки и образования. 2017. № 4. ;URL: https://science-education.ru/ru/article/view?id=26658 (дата обращения: 16.02.2026).



