Процесс обучения представляет собой образовательно значимое взаимодействие учителя и учащихся. До недавнего времени считалось, что для обеспечения успешности этого взаимодействия достаточно создания адекватной учебным целям системы педагогических условий: материально-технических, учебно-методических, организационных.
Сегодня на смену термину «педагогические условия» приходит термин «образовательная среда», поскольку на современном уровне развития информационных и коммуникационных технологий уже больше нельзя гарантировать, что условия, в которых протекает образовательный процесс, находятся в достаточной степени под контролем учителя и администрации школы. В дидактике активно развивается «средово-ориентированный подход к обучению». В этой концепции признается, что основное влияние на ребенка оказывает среда, в которой протекают процессы самообразования и саморазвития ребенка. Учитель и общение с ним является лишь частью окружающей его среды. Моделирование, проектирование и оценка образовательной среды и находится в центре внимания этого подхода.
Теоретические основы данного подхода развиваются сегодня в рамках целого ряда авторских концепций. В России наибольшую известность приобрели научные школы Ю.С. Мануйлова [1, с. 2] и В.А. Ясвина [2].
Каждая из этих теорий утверждает, что имеется потенциальная возможность проектирования среды, ориентированной на достижение различных образовательных целей. С этих позиций мотивирующая образовательная среда (МОС) – это образовательная среда творческого типа, оказывающая влияние на активизацию имеющихся у учащихся мотивов учения, предоставляющая возможности достижения учебной цели, эмоционального подкрепления актуализированных мотивов в результате достижения цели и становления на их основе новых.
Именно созданием такой среды системы дополнительного математического образования учащихся Архангельской области мы и занимались для решения проблемы повышения мотивации учащихся.
Значимость решения этой проблемы признана в России на официальном уровне. Именно с её описания начинается перечень проблем, на решение которых направлена принятая 23 декабря 2013 года Концепция развития математического образования в Российской Федерации [3].
Возможности для развития мотивации к изучению математики обеспечивает с точки зрения теории В.А. Ясвина совокупное влияние нескольких компонентов образовательной среды: пространственно-предметного, социального и психодидактического (таблица).
Роль компонентов МОС в развитии учебной мотивации
|
Элементы МОС |
Проектирование |
|
Пространственно-предметный |
Условия проявления естественных мотивов любопытства и любознательности за счет внешней привлекательности, необычности, неожиданности объектов и средств деятельности. Порождение мотивов самореализации представлением свободы пространственного и предметного выбора |
|
Социальный компонент (человеческий фактор) |
Условия проявления социальных мотивов за счет создания ситуаций: взаимопомощи, партнерства в удовлетворении образовательных потребностей. Предоставление возможности «заражения» познавательными интересами и ценностями |
|
Технологический (психодидактический) компонент |
Обеспечение возможности переноса мотивов на учение с сопряженной деятельностью. Создание условий подкрепления мотивов учения через ситуации успеха, достижения |
Опишем каждый из них в отдельности.
В качестве главного компонента, пространственно-предметного, мы выбрали экспериментальную математику – новую научную область, специфика которой состоит в широком использовании компьютерных экспериментов на разных этапах исследования. Именно эта предметная область сегодня признается наиболее перспективной для создания условий повышения мотивации учащихся. Приведем в доказательство цитату из резолюции III Всероссийского съезда «Школьное математическое образование»: «Экспериментальный, исследовательский подход к изучению математики является перспективной мировой тенденцией. Такой подход, за счет повышения мотивации, содействует выбору учащимися продолжения образования в направлениях, требующих повышенного уровня математических знаний. Он особенно эффективен при использовании компьютерных инструментов и сред. Целесообразно рекомендовать для включения в примерные основные образовательные программы на всех уровнях образования в части предмета "Математика" использование компьютерных инструментов математической деятельности» [4].
Для того чтобы сделать МОС доступной для учащихся, проживающих в различных городах, была создана сеть пилотных площадок с ресурсным центром – лабораторией проекта «Методики и информационные технологии в образовании» (MITE) в САФУ имени М.В. Ломоносова. Задача ресурсного центра состояла в создании сайта кружка «Экспериментальная математика» и наполнении его учебными и методическими материалами для организации исследовательской деятельности учащихся в области экспериментальной математики [5]. На этом сайте постепенно формируются несколько коллекций:
- коллекция контекстно поставленных исследовательских задач экспериментальной математики, каждая из которых может стать предметом обсуждения на занятиях или самостоятельного решения;
- коллекция видеозаписей научно-популярных лекций ведущих специалистов в области экспериментальной математики;
- коллекция презентаций отчетов учащихся о ранее выполненных исследовательских работах;
- коллекция индивидуальных достижений учащихся.
В дополнение к этому сами учащиеся создали группу в социальной сети «ВКонтакте» для неформального общения (обсуждать решение задач, презентации, фотоотчеты с конкурсов, турниров, совместных мероприятий). Еще одним элементом данного компонента стало создание учащимися своего видеоканала [6] на YouTube для демонстрации образовательных роликов по экспериментальной математике собственного изготовления, а также фильмов о впечатлениях, полученных от участия в финале международного конкурса «Математика и проектирование» (рис. 1).
Рис. 1. Видеоканал, созданный членами кружка «Экспериментальная математика»
В дополнение к этому для обеспечения возможности экспериментальной деятельности учащихся в ходе постановки и решения задач каждая из пилотных площадок создала свой набор ресурсов. В САФУ имени М.В. Ломоносова члены кружка имели возможность пользоваться оборудованием, установленным в лаборатории проекта MITE: персональными компьютерами и ноутбуками с установленными на них системами динамической математики: GeoGebra, «1С: Математический конструктор» и «Живая математика», интерактивной доской, системой электронного голосования. Занятия в лаборатории также обеспечивали учащимся свободный доступ к ресурсам Интернета во время занятий и индивидуальной работы. Кроме того, деятельность учащихся по работе с каждой контекстно поставленной исследовательской задачей была обеспечена четырьмя видами оборудования: 1) игровое оборудование для организации настольной игры или игры на местности на этапе постановки задачи; 2) оборудование для проведения экспериментов с вещественными моделями математических объектов на этапе докомпьютерного решения задачи; 3) рабочие динамические листы для обеспечения деятельности учащихся в зоне ближайшего развития при проведении компьютерных экспериментов на этапе компьютерного решения задачи; 4) оборудование для мотивации поиска дедуктивного доказательства экспериментально установленных фактов и организации деятельности учащихся в зоне ближайшего развития на этапе поиска доказательства.
Перейдем теперь к описанию социального компонента мотивирующей образовательной среды. Он представляет собой специально созданное дополнение к социальному окружению учащегося (субъекта образования). Мы постарались включить в него людей, увлеченных экспериментальной математикой, обеспечили ученику возможность общения с этими людьми. В их число мы включили ученых – математиков, которых пригласили для чтения научно-популярных лекций (С.И. Гроздева, А.В. Ястребова, В.Н. Дубровского), студентов, которые представили учащимся интерактивную выставку «История экспериментов в математике».
Наиболее важным компонентом мотивирующей образовательной среды является психодидактический (или технологический) компонент – содержание, характер и организация учебных стимулов, учебной деятельности и учебного взаимодействия. В отличие от остальных компонентов, активизирующих привычные мотивы, он направлен на создание условий для постепенного становления на их основе мотивов учебно-исследовательской деятельности и их развития.
Данный компонент представлен методикой исследовательского обучения с использованием систем динамической математики. Процесс решения исследовательской задачи экспериментальной математики можно представить в виде универсальной модели, названной нами «Ромашкой» (рис. 2), центр которой представляет собой этапы решения исследовательской задачи, основанные на пяти этапах «полного акта мышления» исследователя (по Дж. Дьюи).
На любом из этих этапов учащийся имеет возможность перейти к реализации цикла экспериментальной математики: постановка задачи – обоснование привлечения компьютерного эксперимента – планирование компьютерного эксперимента и моделирование объекта исследования, сбор данных, анализ данных, использование результатов компьютерного эксперимента для решения задачи, развитие идеи решенной задачи. Такой переход может осуществляться несколько раз в ходе решения одной задачи.
В зависимости от места компьютерного эксперимента в структуре процесса решения исследовательской задачи выделяются: конструктивный (на этапе идентификации проблемы), поисковый (анализ проблемы), верифицирующий (выдвижение гипотез), контрольный (доказательство) и модифицирующий (оценка результатов) компьютерный эксперимент.
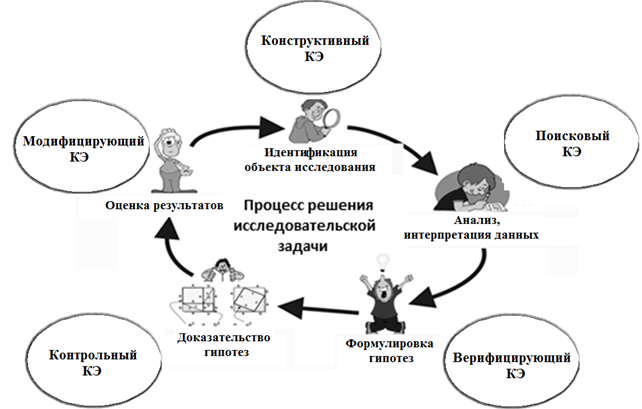
Рис. 2. Общая схема решения исследовательской задачи с использованием циклов экспериментальной математики
Место и количество выходов на цикл экспериментальной математики определяется как характером решаемой задачи, так и уровнем теоретической подготовки учащихся, богатством имеющихся в их арсенале эвристических средств теоретического поиска и стилем мышления.
Роль учителя при работе ученика над решением исследовательской задачи экспериментальной математики состоит в создании таких условий обучения, при которых ученик может получить своевременную помощь при выходе в зону своего ближайшего развития, прочувствовать как ситуацию успеха даже маленькое продвижение в решении исследовательской задачи. Для этих целей учитель использует приемы геймофикации, бейджинга, технику коучинга, сократовскую беседу, элементы проектного обучения, методы коллективного творчества, оргдеятельностной игры и др. Методы и средства помощи учащимся подбираются в соответствии с уровнем исследовательского обучения, отнесенным к зоне ближайшего развития учеников. Низшим является уровень контрольного исследования, на котором учитель демонстрирует образцы исследовательской деятельности, вовлекая ученика в следование этим образцам для проверки правильности выводов. Здесь применяются средства визуализации интеллектуальной деятельности и ее оснований: проблемное изложение, анимации, интеллект-карты, манипуляторы. Данный уровень формирует первые представления учащихся о специфике исследовательской деятельности, о языке исследователя. Данный уровень позволяет ученикам достичь успеха в роли критика: уточнить выводы, обнаружить несоответствия: выбросы в данных, неадекватность модели, пробелы в рассуждениях и т.п. Следующий уровень - структурное исследование. Он предполагает строгое следование плану и инструкциям педагога. Это позволяет сформировать у учащихся универсальные исследовательские действия исполнительского характера. Данный уровень дает возможность ученикам достичь успеха в сборе необходимой информации, полезной систематизации собранных данных, в выдвижении значимых идей и др. Третий уровень - уровень управляемого исследования. Здесь учащиеся уже не получают прямых указаний от учителя. Учитель оказывает помощь учащимся через использование готовых виртуальных лабораторий с ограниченным набором инструментов, а также через вовлечение учащихся в эвристическую или сократовскую беседу. На этом уровне ученики осваивают универсальные исследовательские действия, позволяющие планировать и осуществлять саморегуляцию исследовательской деятельности. Ситуация успеха на этом уровне – это постановка задачи, разработка исследовательской программы, определение критериев оценки полученных результатов и др. Высший уровень – открытые (истинные) исследования - реализуется с применением технологии коучинга. Здесь учитель выступает в роли консультанта, который влияет на исследовательскую деятельность учащихся на уровне ее личностной и интеллектуальной рефлексии. Он помогает ученику осознать сильные и слабые стороны своего когнитивного стиля, актуального уровня сформированности исследовательских действий, обнаружить существования иных подходов на основе самоанализа неудач и наметить новые горизонты в работе над исследованием.
Важным элементом технологии исследовательского обучения являются конкурсы: 1) международный конкурс исследовательских проектов учащихся «Математика и проектирование» [7]; 2) турнир по экспериментальной математике [8]. Такой комплекс конкурсных мероприятий предоставляет равные возможности учащимся с разными стилевыми особенностями. В первом будут успешны те учащиеся, которые обладают так называемым медленным умом. Во втором – учащиеся, обладающие «быстрым умом».
Эффективность созданной нами мотивирующей образовательной среды подтверждается появлением все новых и новых школ, на базе которых организованы кружки экспериментальной математики, постоянным ростом числа участников всех проводимых мероприятий, стихийным развитием практики наставничества в среде кружковцев.
Библиографическая ссылка
Шабанова М.В., Николаев Р.Н., Павлова М.А. ОПЫТ СОЗДАНИЯ МОТИВИРУЮЩЕЙ ОБРАЗОВАТЕЛЬНОЙ СРЕДЫ В ПРЕДМЕТНОМ ПОЛЕ ЭКСПЕРИМЕНТАЛЬНОЙ МАТЕМАТИКИ // Современные проблемы науки и образования. 2017. № 4. ;URL: https://science-education.ru/ru/article/view?id=26578 (дата обращения: 16.02.2026).



