Развитие когерентно-стохастической культуры студентов технического вуза
В технических и социально-экономических системах профессионал постоянно сталкивается с множеством процессов, которые не могут быть восприняты однозначно и детерминированно. Их проявление и появление связано с множеством случайных причин. Для прогнозирования поведения сложных технических систем исследователю постоянно приходится учитывать влияние множества факторов. Причем эмпирические величины, необходимые для построения математических моделей и на их основе систем, могут быть получены различными путями с помощью различных измерителей с разной степенью точности. Вопросы количественного измерения возникают не только в технических системах. Сейчас с ними постоянно сталкиваются социологи, экономисты, специалисты в области принятия решений. Подобные проблемы возникают и в других областях деятельности человека. Можно ли доверять полученным данным? И если «да», то с какой долей вероятности? Интересы развития всех направлений науки требуют корректного и методически обоснованного введения в техническое образование элементов стохастической культуры.
Под стохастической культурой будем понимать интегративное качество личности, позволяющее моделировать процессы и явления в технических и социально-экономических системах, а также выстраивание субъектной позиции на основе вероятностной оценки событий. Чем обусловлена необходимость обращения к ней?
Эта необходимость обусловлена, во-первых, высоким уровнем развития современной науки. Известно, что естественные, гуманитарные и технические науки во многом опираются на статистические концепции, широко и продуктивно используют современные вероятностно-статистические методы. Эта необходимость диктуется также социально-экономическими потребностями общества, народным хозяйством – промышленным производством, сельским хозяйством, транспортом, связью, военным делом, здравоохранением и т.д. Кроме того, специфика технических дисциплин состоит в том, что они в большинстве своем опираются на заранее неизвестные (константные) значения. В действительности исходные данные, на основе которых осуществляются расчеты, содержат неизбежные погрешности. Методика их получения очень различна и допускает лишь вероятностную оценку точности. Исследование протекания технико-экономических и технологических процессов исторически использует методы моделирования. Любая модель, по сути, абстрактна и, следовательно, неполна, так как, выделяя основные свойства, определяющие те или иные закономерности поведения объекта, мы абстрагируемся от других свойств. Последние, несмотря на относительную малость, могут не только определить отклонения в поведении объекта, но изменить тенденцию поведения. Кроме того, присутствует и чисто субъективный фактор, связанный с ранжированием объективных показателей процесса, основанный на личном опыте и предпочтениях исследователя.
Стохастика представляет собой язык описания реальных жизненных ситуаций, возникающих во всех сферах человеческой жизнедеятельности.
Проблема состоит в овладении будущим специалистом этим языком. Сошлемся на мнение известного педагога-математика А.Н. Колмогорова: «Представленную проблему можно было бы переформулировать так: какова должна быть математическая подготовленность нематематика-инженера (курсив - Н. Ч.), желающего использовать в своей работе вероятностно-статистические методы? Этот вопрос приобретает особую остроту в связи с тем, что широкое развитие вычислительной техники позволяет обращаться к программам совсем не подготовленным пользователям. Опасность такого рода деятельности состоит в том, что прикладная математика все же всегда остается дедуктивной наукой. Модель нельзя получить непосредственно из экспериментальных данных, не опираясь на предпосылки, привносимые исследователем. Скажем, нужно отчетливо понимать, что результаты кластер-анализа всегда несут в себе некоторую неопределенность – они зависят от метрики пространства, сконструированного исследователем (т.е. от выбора шкал, в которых представляются измерения)».
Отметим также необходимость для современного инженера обращения к программному обеспечению (ПО) с учетом оценки надежности и вероятности безотказной работы. В настоящее время стоимость ПО в отдельных отраслях намного превышает стоимость аппаратных средств. Инженеру необходимо знание текущего состояния надежности ПО, поскольку можно более уверенно определить время до полного завершения его испытания и передачи его в эксплуатацию. Эти знания могут быть также полезны и руководителю при принятии решения по наилучшему распределению ограниченных ресурсов (финансов, кадров) по различным программным модулям на различных этапах жизненного цикла ПО.
Знание текущего и прогнозируемого состояния надежности ПО может быть применено и при распределении затрат между надежностью, стоимостью, а также при выборе оптимального решения для получения наиболее надежного ПО заданной стоимости.
Таким образом, подготовка будущего инженера должна строиться на принципе взаимности-когерентности стохастического моделирования прикладных задач. В.А. Далингер [3], отмечая учебную роль прикладных задач, говорит о необходимости связывания математических понятий с их реальными прототипами. Л.Ю. Березина и И.А. Лурье [2], отмечая воспитательную роль прикладных задач, указывают, что интерес к производительному труду развивается при решении задач, построенных на фактических данных, заимствованных из производственной деятельности. В.Д. Селютин, говоря о возможностях стохастики [6], отмечает, что учебные задачи должны строиться на реальных внематематических ситуациях. Конкретные объекты используются в качестве «сырья» [6] для создания математических моделей. Затем математические модели используются для «исследования фрагментов действительности, содержащих подобное сырье». Преподавателям технических вузов приходится считаться с тем, что школьная математика использует детерминированный подход, который предполагает, что исходная информация однозначно описывает внешние воздействия и состояние системы, что позволяет найти единственное оптимальное решение.
Детермированные модели сравнительно просты и дают возможность относительно легко найти решение. При детерминированном подходе критерий оптимальности и уравнения, описывающие состояние управляемого объекта, а также внешние воздействия считаются известными [4]. Однако уже выпускники школ должны отчетливо понимать, что в природе и общественной жизни далеко не все процессы сводятся к детерминированным, что такого рода подход является только первым приближением к действительности. Следующий шаг на пути познания – стохастический подход.
Таким образом, мы приходим к требованиям, которые должны быть предъявлены к понятию «стохастическая учебная задача». Это понятие:
1) должно быть логично включено в общую концепцию математического образования в вузе и давать студентам представление как об общей методологии математического исследования, так и об особом характере статистического исследования;
2) должно повышать личную мотивацию и ответственность студента за результат познания реальной действительности. Такие задачи дисциплинируют ум, развивают логическое мышление, воспитывают аккуратность в рассуждениях и вычислениях;
3) должно отражать субъектную позицию студента, отражать индивидуальность в выборе и принятии решения;
4) должно отражать тесную взаимосвязь различных разделов математики и систематическое объединение вычислительных, аналитических и геометрических методов с целью анализа случайных событий в науке и технике;
5) должно содержать фрагмент реальной действительности и отражать многообразие подходов к ее решению;
6) должно содержать требование проверки адекватности ее решения и границ доверительного интервала.
С учетом данных требований определим «стохастическую учебную задачу» как особого рода задачу с жизненно-практическим содержанием, представляющую собой математически сформулированную модель проблемной стохастической ситуации, гомоморфно [8] отображающую объект исследования.
Стохастическая проблемная ситуация – это реальная жизненная ситуация, связанная с анализом явлений, происходящих под воздействием случайностей. Среди стохастических задач особое место принадлежит когерентно-стохастическим задачам. Эти задачи способны успешно интегрироваться в структуру традиционного вузовского курса математики и эффективно решать проблему развития внутрипредметных связей различных его тем и разделов в полном соответствии с требованиями когерентно-интегративного подхода. Новое понятие «когерентно-стохастическая задача», по мнению Л.А. Тереховой [7], должно удовлетворять целому ряду дополнительных требований:
1) когерентно-стохастические задачи должны быть сформулированы таким образом, чтобы могли быть включены в классическую схему курса (курсив - Н. Ч.) математики без ущерба для образовательного стандарта;
2) когерентно-стохастические задачи должны способствовать включению новых понятий и повторению ранее изученных традиционных тем;
3) когерентно-стохастические задачи должны служить действенным средством укрепления внутрипредметных связей математики [1].
Наши многолетние исследования и большой эмпирический материал позволили сформулировать методологический [10], инструментальный [11; 13; 14] и прикладной [5; 12] аспекты теории стохастического моделирования реальных технико-экономических и технологических задач. Нами установлено и доказано, что построенные на проблемных ситуациях стохастические модели обеспечивают минимальную степень детализации процесса, поскольку описывают не сами физические явления, а только внешние проявления взаимосвязей между условиями и результатом процесса в предположении случайного характера этих взаимосвязей. Следует отметить, что, в отличие от детерминированных математических моделей, стохастические не отвечают на вопрос «почему?» в отношении выявленных при моделировании взаимосвязей. Здесь возможен ответ только на вопрос «сколько?» с обязательным подтверждением достоверности количественной оценки.
Нужно четко осознавать, например, что оценки коэффициентов регрессии в стохастических моделях всегда оказываются смещенными в силу невозможности включения в модель всех независимых объясняющих переменных. Можно поставить задачу и шире: «всегда ли адекватны изучаемой ситуации исходные положения фишеровской концепции математической статистики?» [1]. Неоднозначность в оценке реальных событий заставляет исследователя глубже проникать в физическую сущность задачи.
Развитие подходов к инженерной оценке реальных технико-экономических и технологических систем можно условно представить в виде следующей схемы.
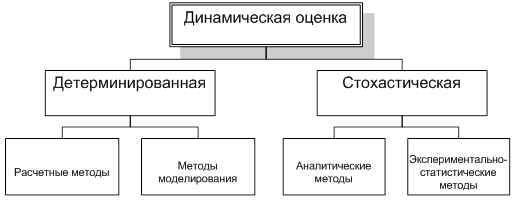
Подходы к оценке реальных технико-экономических и технологических систем
Особую сложность и интерес вызывают задачи, связанные с необходимостью оценивания альтернатив решения на основе мнений экспертов. При решении рассмотренных задач все множество проблем можно разделить на два класса: с достаточным и недостаточным информационным потенциалом. Для проблем первого класса имеется необходимый объем знаний и опыта, по их решению и эксперты могут считаться качественными источниками и достаточно точными измерителями информации. Для таких проблем обобщенное мнение группы экспертов определяется осреднением их индивидуальных суждений и является близким к истинному. Результаты экспертизы при решении проблем второго рассматриваемого класса не могут быть получены простым осреднением множества экспертных суждений, поскольку мнение одного эксперта может оказаться правильным, хотя оно сильно отличается от мнения всех остальных экспертов.
Проблема включения реальных (или квазиреальных) задач в учебную среду вуза существенно усложняется не столько исходя из математической постановки задачи, поскольку методы построения моделей достаточно представлены в специальной литературе, сколько из-за сложности (или отсутствия) получения достоверных опытных данных и опыта анализа и прогноза результатов моделирования.
Однако, несмотря на сложности включения подобных задач в учебный процесс вуза, отметим плодотворность их влияния на формирование стохастической культуры студентов. Подобный класс задач позволяет:
− сформировать у студентов понимание стохастической сущности прикладных задач;
− обусловить взаимодействие студентов с внешними стохастическими условиями и факторами техно-экономической среды;
− оценивать результаты исследований, сравнивать новые экспериментальные данные с данными принятых моделей для проверки их адекватности и при необходимости предлагать изменения для улучшения моделей;
− проектировать индивидуальные исследовательские траектории на основе учета трендовых и случайных стохастических факторов.
Библиографическая ссылка
Чигиринская Н.В. ОБЩИЕ ПРИНЦИПЫ КОНСТРУИРОВАНИЯ КОГЕРЕНТНО-СТОХАСТИЧЕСКИХ УЧЕБНЫХ ЗАДАЧ КАК СРЕДСТВА РАЗВИТИЯ СТОХАСТИЧЕСКОЙ КУЛЬТУРЫ СТУДЕНТОВ ТЕХНИЧЕСКОГО ВУЗА // Современные проблемы науки и образования. 2017. № 1. ;URL: https://science-education.ru/ru/article/view?id=26139 (дата обращения: 12.02.2026).



