Одна из актуальных задач современного высшего образования – это развитие личности студентов. Не только магистры и специалисты, но и бакалавры должны обладать высоким уровнем развития исследовательской компетентности (ИК) в связи с социально-экономическими изменениями, постоянно происходящими в нашей стране. А значит, при организации образовательного процесса необходимо акцентировать внимание именно на непрерывном развитии этого интегративного качества личности студентов для разных направлений их профессиональной подготовки. Важно нестандартно подходить к организации образовательного процесса, управлению им, максимально задействовать весь потенциал фундаментальных дисциплин, которые можно выделить для любого направления подготовки, если перед преподавателями ставится цель развить исследовательскую компетентность студентов.
Следуя научной идее, предложенной в [6] и связанной с тем, что достижение планируемых результатов развития исследовательской компетентности можно прослеживать на основе овладения студентами учебно-исследовательскими и научно-исследовательскими компетенциями, соотнесенными с уровнями обучения (бакалавриат и магистратура), в качестве основного дидактического средства развития ИК выбран комплекс исследовательских задач: недоопределенные, с избыточными данными, обратные, на составление структурно-логических блок-схем, практической направленности, на доказательство, оценочно-аналитические, проектно-технологические [3, 4, 6, 7].
Целью работы является выделение уровней сложности исследовательских задач и определение вариантов последовательностей их предъявления в учебном процессе для эффективного развития исследовательской компетентности студентов вуза.
Механизмом развития исследовательской компетентности является включение студентов в постепенно усложняющуюся исследовательскую деятельность, связанную с решением исследовательских задач и выполнением учебных исследований [9]. Движение от теоретических знаний к практическим умениям и навыкам, а, следовательно, переход от учебно-исследовательского типа деятельности к научно-исследовательскому происходит в результате последовательного освоения трех форм учебной деятельности [1, 2, 8]:
1) знаково-отражательной с преобладанием объяснительно-иллюстративного, алгоритмического методов обучения и форм обучения: лекции, семинары, группы поддержки, факультативы;
2) практико-моделирующей с преобладанием метода проблемного изложения материала, частично-поискового метода и форм обучения: научные семинары, учебные мини-конференции;
3) проективной с преобладанием поискового метода, метода проектов и форм обучения: научные студенческие конференции.
В связи с этим основой для выделения типов исследовательских задач, уровней их сложностей и последовательностей их предъявления в учебном процессе служит принцип постепенного освоения студентами приемов, этапов исследовательской деятельности и последовательного движения в предметной области или предмете.
В результате нашей работы мы выделили 3 основные последовательности предъявления задач в учебном процессе, связанные с изучением:
1) одной учебной дисциплины;
2) блока учебных дисциплин одного цикла;
3) блока учебных дисциплин одного цикла с учетом каждой учебной дисциплины, входящей в данный блок, ее общих разделов и отдельных тем.
Независимо от выбранного варианта предъявления необходим учет индивидуальных образовательных траекторий студентов.
Следуя логике нашего исследования, соотнесем типы исследовательских задач и их уровни с основными видами деятельности. В зависимости от того, в рамках какой предметной области рассматриваются задачи, они наполняются соответствующим содержанием. Мы приведем конкретные примеры разноуровневых исследовательских задач с учетом их предъявления в рамках изучения математических дисциплин одного цикла для студентов направления «Математическое обеспечение и администрирование информационных систем». Выбор математических дисциплин был обусловлен их развивающими возможностями [5].
Знаково-отражательная деятельность
Задачи на составление структурно-логических блок-схем (тем, разделов, предметов, доказательств утверждений, теорем, алгоритма решения стандартных и нестандартных задач) направлены на развитие умений анализировать и синтезировать, следить за логикой, структурировать учебный материал, выявлять главное. Основные дисциплины: математический анализ, векторная алгебра, линейная алгебра, дискретная математика.
Уровни задач
1. Составление блок-схем алгоритма решения учебной задачи.
Пример (дисциплина «Линейная алгебра»): составить блок-схему вычисления обратной матрицы.
2. Составление блок-схем алгоритма доказательства утверждения, теоремы.
Пример (дисциплина «Математический анализ»): составить блок-схему доказательства теоремы «О единственности предела сходящейся последовательности».
3. Составление блок-схем лекций, тем, разделов, исследовательских работ, дисциплины.
Пример (дисциплина «Векторная алгебра»): составить блок-схему к теме «Приложения задач векторной алгебры».
Обратные задачи с известным методом решения и результатом, необходимые для установления исходных данных или проверки корректности данных. Решение обратных задач направлено на развитие гибкости мышления, сообразительности. Студенты овладевают обратными операциями, учатся разнообразным способам проверки результатов.
Уровни задач
1. Проверка решения с помощью известной обратной операции.
Пример (дисциплина «Линейная алгебра»): проверить правильность нахождения решений системы линейных уравнений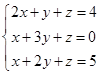 
.
2. Восстановление исходных или недостающих данных.
Пример (дисциплина «Векторная алгебра»): при каком значении n вектор 
единичный? Найти его направление.
3. Получение или интерпретация исходных данных по известной информации.
Пример (дисциплина «Векторная алгебра»): даны векторы 
и 
. Найти их векторное произведение, если известно, что вектора ортогональны.
Недоопределенные задачи и задачи с избыточными данными развивают внимание студентов к исходным данным, способствуют развитию умений выделять главное, определять достаточность (необходимость) условий, дают ценную практику в постановке задач.
Уровни
1. Задачи на обнаружение недостающих данных, обнаружение явно лишних или неявно лишних условий с помощью некоторых указаний.
Пример (дисциплина «Векторная алгебра»): даны 3 вектора: 
, 
, 
. Найти площадь треугольника АВС. Есть ли в условии задачи явно лишние данные?
2. Обнаружение неявно лишних условий при отсутствии указаний или задачи с недостающими качественными характеристиками (решить в предположении, что….).
Пример (дисциплина «Математический анализ»): найти массу М дуги кривой 
.
3. Избыточно-противоречивые условия задач, выявление областей, в которых задачи являются доопределенными.
Пример (дисциплина «Математический анализ»): вычислить двойной интеграл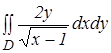
, если область D ограничена линиями: 
.
Практико-моделирующая деятельность
Задачи на доказательство (аксиоматические доказательства, доказательство от противного, метод математической индукции, дедуктивные доказательства, метод логических рассуждений, аналитические доказательства) развивают алгоритмическое мышление, способность выдвигать гипотезы, аргументированно обосновывать свои предположения. Основные дисциплины: математический анализ, дискретная математика, аналитическая геометрия, теория чисел, теория вероятностей, линейная алгебра.
Уровни задач
1. По образцу (воспроизведение, повторение).
Пример (дисциплина «Аналитическая геометрия»): доказать, что уравнение 
является уравнением плоскости.
2. На применение (вывод промежуточных формул, доказательство утверждений в процессе решения задач практического содержания).
Пример (дисциплина «Математический анализ»): доказать, что 
.
3. Распространение доказательств на случай с измененными условиями (большее число переменных, добавление новых ограничений и т.д.).
Пример (дисциплина «Теория вероятностей»): доказать закон больших чисел в форме Бернулли (как следствие доказательства закона больших чисел в форме Чебышева).
Задачи практической направленности помогут студентам использовать предметные знания в будущей профессиональной деятельности, осознать и понять тесную связь изучаемого предмета с жизнью, с основами других наук.
Уровни задач
1. Задачи практической направленности.
Пример (дисциплина «Теория чисел»): предположим, что издержки получения питьевой воды заданы формулой 
, где 
— процентное содержание загрязняющих воду примесей. Найти скорость изменения издержек производства, если примеси составляют 5%.
2. Перевод задачи с языка предметной области на язык математики и ее решение.
Пример (дисциплина «Теория вероятностей»): в театре, вмещающем 900 зрителей, два гардероба. На сколько мест должен быть рассчитан каждый гардероб, чтобы в среднем в 99 случаях из 100 каждый зритель мог раздеться в выбранном гардеробе?
3. Интерпретация результатов (например, перевод с математического языка на язык предметной области).
Пример (дисциплина «Теория вероятностей»): урожайность кормовой свеклы с 1 га равна 30 т с вероятностью 0,1; 35 т с вероятностью 0,15; 40 т с вероятностью 0,2; 45 т с вероятностью 0,3, 50 т с вероятностью 0,1 и 60 т с вероятностью 0,1. В каких пределах с вероятностью 0,95 будет находиться урожай, если свеклой засажено 37 га? Какое наименьшее количество гектаров необходимо выделить для посадки свеклы, чтобы с вероятностью не менее 0,975 урожай был не менее 570 т?
Проективная деятельность
Оценочно-аналитические задачи способствуют развитию умений анализировать, использовать теоретический материал, давать критические оценки своей и чужой работе. Основные дисциплины: дифференциальные уравнения, функциональный анализ, теория вероятностей, математическая статистика.
Уровни задач
1. Анализ условия задачи, оценка хода решения и результата решения.
Пример (дисциплина «Дифференциальные уравнения»): найти семейство линий, у которых отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью ординат.
2. Формулирование, анализ и оценка результатов решения задачи, саморецензирование.
Пример (дисциплина «Функциональный анализ»): пусть имеются две дороги (непрерывные кривые на плоскости, содержащие концы) 
и 
. По дорогам движется машина (точка), поливая их. Будем считать, что машина поливает вокруг себя площадь замкнутого круга, причем радиус полива можно менять. Найти наименьший радиус, при котором при движении машины по одной из дорог будут политы обе.
3. Рецензирование, оппонирование исследовательских задач или исследовательских работ студентов.
Пример (дисциплина «Дифференциальные уравнения»): записать а) линейное и б) нелинейное дифференциальные уравнения третьего порядка, частным решением каждого из которых является функция 
.
Проектно-технологические задачи необходимы для развития умений выдвижения гипотез, составления плана исследования, использования известных методов, способностей обобщать, делать выводы, оформлять и представлять результаты исследований.
1. Выполнение стандартных процедур исследования: выдвижение гипотезы, составление плана исследования, проведение исследования (в наличии пошаговая инструкция).
Пример (дисциплина «Математическая статистика»): из 200 задач первого семестра курса математического анализа, предложенных для решения, студенты решили 130, а из 300 задач второго семестра студенты решили 120. Можно ли при α=0,01 утверждать, что материал первого семестра дисциплины «Математический анализ» студенты усвоили лучше, чем второго?
2. Осуществление самостоятельного планирования и решения стандартной задачи в рамках учебной дисциплины (задачи предлагаются преподавателем).
Пример (дисциплина «Математическая статистика»): используя данные Российского статистического ежегодника, выбрать показатели, связанные линейной регрессионной зависимостью, с коэффициентом корреляции не менее 0,6.
3. Самостоятельный поиск данных (для предложенной или самостоятельно сформулированной задачи) и полностью самостоятельное проведение исследования.
Темы проектов
1. Математическая модель численности населения.
2. Предельный анализ в экономике.
3. Распределение Парето.
Построение учебной деятельности в рамках учебной дисциплины или блока дисциплин с учетом выделенных уровней сложности исследовательских задач и предложенных вариантов их предъявления дало положительные результаты при обучении студентов направлений: «Математическое обеспечение и администрирование информационных систем», «Педагогическое образование» и некоторых других Тюменского государственного университета. Проделанная опытно-экспериментальная работа показала, что по окончании каждого этапа обучения студенты смогли овладеть следующими основными учебно-исследовательскими и научно-исследовательскими компетенциями:
в знаково-отражательной деятельности: способностями к сбору и сопоставлению данных для решения учебных задач; самостоятельностью в освоении новых способов пополнения знаний; способностями к анализу и синтезу; способностями к продуцированию идей, выдвижению гипотез и их проверке с использованием стандартных алгоритмов или методик; способностями представлять и защищать результаты решений учебно-исследовательских задач на учебных занятиях;
в практико-моделирующей деятельности: способностями к сбору и сопоставлению данных для написания учебных исследовательских работ (докладов, рефератов, аннотаций и др.); способностями к самостоятельному освоению новых способов пополнения знаний, например с помощью информационных технологий; способностями к продуцированию идей, выдвижению и проверке гипотез с использованием стандартных и нестандартных алгоритмов или методик; способностями представлять и защищать результаты своей учебно-исследовательской работы не только на учебных занятиях, но и на учебных мини-конференциях, фестивалях науки;
в проектно-технологической деятельности: способностями к пониманию и умениями обосновать актуальность, новизну, теоретическую и практическую значимость проводимого исследования; способностями к проведению исследования по подробной предложенной, стандартной или самостоятельно разработанной схеме; способностями к анализу готовых или полученных результатов своих и чужих исследований, написанию развернутых рекомендаций; способностями к составлению прогнозов, формулированию выводов; способностями к представлению и защите результатов своей работы на всевозможных научных мероприятиях (научных семинарах, защитах курсовых и выпускных квалификационных работ, выступлениях на научных студенческих конференциях).
Библиографическая ссылка
Гайдамак И.В., Панарина С.Н., Сапожникова А.В., Яковлева Н.Л. УРОВНИ ИССЛЕДОВАТЕЛЬСКИХ ЗАДАЧ И ПОСЛЕДОВАТЕЛЬНОСТИ ИХ ПРЕДЪЯВЛЕНИЯ В УЧЕБНОМ ПРОЦЕССЕ ДЛЯ РАЗВИТИЯ ИССЛЕДОВАТЕЛЬСКОЙ КОМПЕТЕНТНОСТИ СТУДЕНТОВ // Современные проблемы науки и образования. – 2016. – № 6. ;URL: https://science-education.ru/ru/article/view?id=25688 (дата обращения: 19.04.2024).