Согласно Концепции развития математического образования РФ, утвержденной Правительством РФ в 2013 году, одна из целей основного общего и среднего образования – обеспечение необходимого стране числа выпускников, математическая подготовка которых достаточна для продолжения образования в различных направлениях и для практической деятельности, включая преподавание математики, математические исследования [11]. Система школьного математического образования должна обеспечить расширенное производство кадрового потенциала, способного осуществлять на современном и перспективном уровне научно-технический прогресс во всех областях принципиальной применимости всего спектра математических знаний [3]. Эта цель имелась в виду при разделении в 2015 году единого государственного экзамена по математике на профильный и базовый уровни.
Ясно, что содержание и форма итогового экзамен по математике не являются нейтральными независимыми характеристиками для школьного математического образования. Аттестационная процедура ЕГЭ неизбежно влечёт за собой изменения в содержании и методах школьного обучения [3].
Этап анализа результатов ЕГЭ является необходимым условием совершенствования математической подготовки школьников и математического образования в целом. Для повышения качества подготовки учащихся к Единому государственному экзамену профильного уровня подобный анализ целесообразно проводить для всех задач с развернутым ответом, прогнозировать пути предупреждения типичных ошибок участников экзамена [1].
Эта статья посвящена анализу результатов ЕГЭ по математике учащихся Алтайского края, полученных в 2015 году при решении задания 17.
Около 40 % участников ЕГЭ профильного уровня в 2015 году приступили к решению задачи 17, однако три четверти из них получили за попытку лишь нулевой балл. Более детальные результаты представлены на рисунке 1.
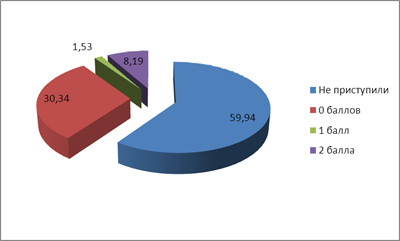
Рис. 1. Результаты выполнения задания 17 в первичных баллах
В профильном ЕГЭ 2015 года модель задачи 17 (ранее – задача С3) претерпела изменения по сравнению с прошлым годом. Вместо системы неравенств была предложена задача: решить «одиночное» неравенство.
Задача 17 (ЕГЭ профильный уровень) в 2015 году предполагала умения учащихся решать уравнения и неравенства [7, 8, 9], а именно: использовать метод введения вспомогательной переменной для решения неравенств; применять метод интервалов; владение тождественными преобразованиями рациональных выражений, а также показательных и логарифмических выражений и умения оценить равносильность этих преобразований; владение понятием области допустимых значений неравенства, системы неравенств, совокупности неравенств, в данном случае связанной со свойствами дробно-рациональной функции; знание свойств показательной и логарифмической функций; понимание смысла системы неравенств как логической операции «конъюнкции» и совокупности неравенств как логической операции «дизъюнкция» и др.
Приведем пример условия задачи 17 одного из вариантов:
«Решите неравенство: 
».
Как следует диаграммы рис.1, процент учащихся Алтайского края, получивших положительный балл (1 или 2) за решение задачи №17 в 2015 году составляет 9,72 %, что несколько ниже нижней границы нормы (10–50 %). Рассмотрим типичные ошибки нынешнего года.
1. Самые распространённые ошибки, сделанных учащимися, приступившими к решению задачи № 17 в 2015 году, связаны с формальным перенесением методов и приёмов решения уравнений на неравенства того же типа. Это, в частности, проявилось в умножение неравенства на выражение с переменной без учёта знака этого выражения, в применении к неравенству свойства пропорции, переход от дробно-рационального неравенства к неравенству, связывающему числители («отбрасывание» знаменателя), замена на первом этапе решения неравенства уравнением. Следующие примеры иллюстрируют указанные ошибки.
Пример 1.
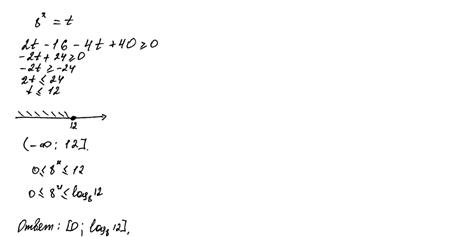
Рис. 2. Умножение неравенства на выражение с переменной
Комментарии: Автором этого решения, представленного на рис. 2, применено неравносильное преобразование, а именно: умножение неравенства на выражение с переменной, знак которого зависит от значения этой переменной. Согласно критериям, оценка – 0 баллов. Заметим также, что в последнем переходе, видимо, ученик допустил описку, вместо 
записав 
. Учитывая эту погрешность, можно констатировать, что автор этого решения не знает также, что неравенство 
верно при всех значениях переменной. Заметим, что последнее замечание нередко встречалось и в других работах.
Пример 2.
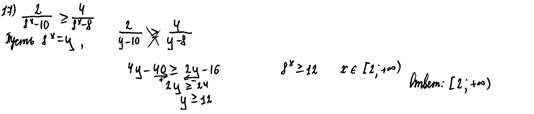
Рис. 3. Применение к неравенству свойств пропорции
Комментарии: Автор этого решения неправомерно применил для неравенства свойство пропорции («крест-накрест»: произведения крайних и средних членов пропорции равны), что проиллюстрировал соответствующим знаком. Имеется также ошибка вычислительного характера в последнем переходе решения. Оценка, согласно критериям, 0 баллов.
Пример 3.
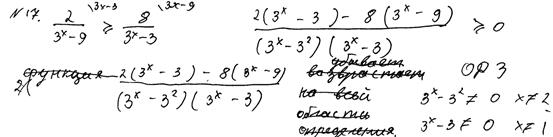
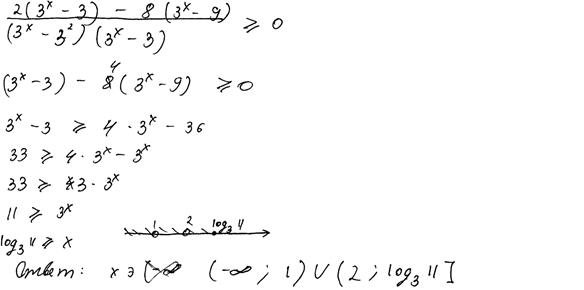
Рис. 4. «Отбрасывание» знаменателя
Комментарии: нарушена равносильность в определённый момент решения. Можно предположить, что ученик использовал в общем случае неверное утверждение о том, что «дробь неотрицательна при неотрицательном числителе». Согласно критериям, 0 баллов.
Заметим также, что в этой работе наблюдается ещё одна достаточно распространённая ошибка: аналитическое и графическое представления ответа не соответствуют друг другу, описывая различные числовые множества.
2. Учащиеся, приступившие к решению задачи №17 и получившие ненулевой балл за эту задачу, применяли в основном метод интервалов, предварительно введя вспомогательную переменную.
С применением метода интервалов и введением вспомогательной переменной связан ряд достаточно распространённых ошибок. Отдельные из них, согласно критериям, могут расцениваться как вычислительные (например, ошибка при определении знака на одном из промежутков), другие – принципиальные, связанные с пропуском шагов алгоритма или неверным их выполнением, не могут быть оценены ненулевым баллом. Приведём примеры.
Пример 4.
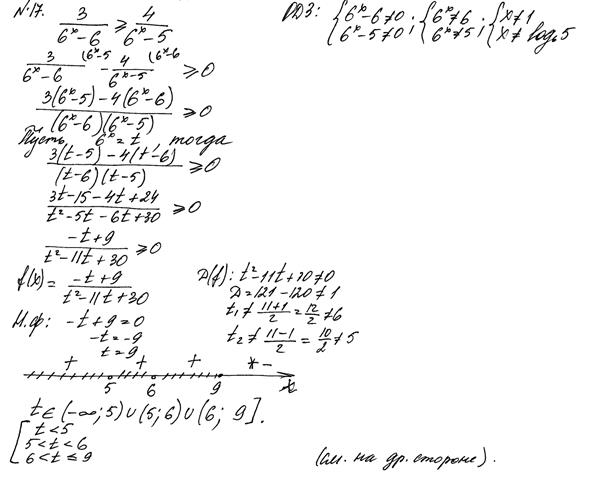
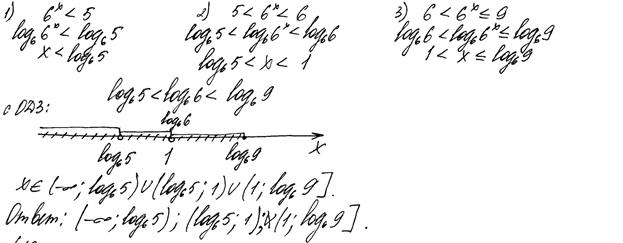
Рис. 5. Ошибка в определении знака на интервале
Комментарии: Ошибка в определении знака на одном из интервалов вполне может быть признана вычислительной. Учащийся довёл решение до конца, продемонстрировав в целом владение методом замены переменных и методом интервалов. Согласно критериям, 1 балл.
Пример 5.
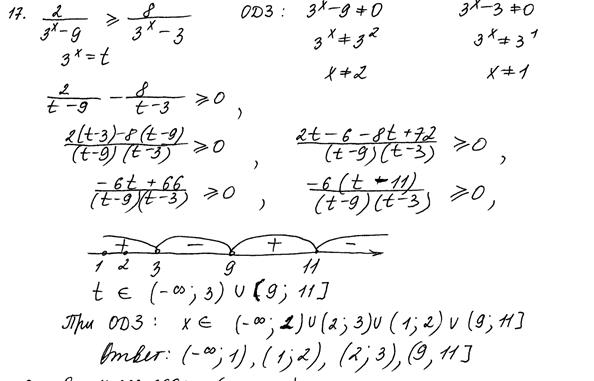
Рис. 8. Отсутствует необходимый шаг алгоритма
Комментарии: Не сделана обратная замена – необходимый шаг алгоритма. На числовой прямой отмечены значения исходной и введённой переменной. Согласно критериям, 0 баллов.
3. Отдельные учащиеся применили так называемый логический способ решения, осуществив на определённом этапе равносильный переход к совокупности двух систем. С этим способом решения неравенства связаны следующие ошибки. Это рассмотрение только одного случая положительности (отрицательности) дроби, неверное использование логической символики. Приведём примеры, иллюстрирующие вторую ошибку.
Пример 6.
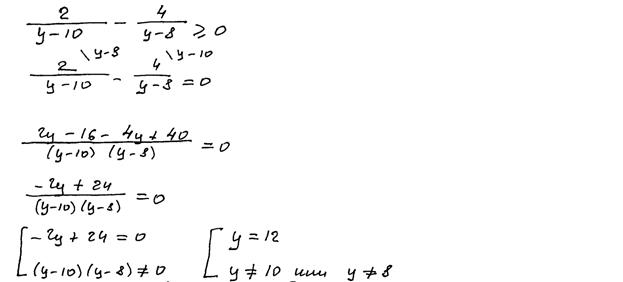
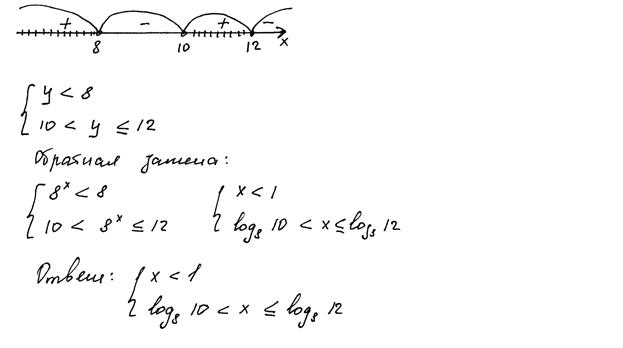
Рис. 7. Неверное использование логической символики
Комментарии: В представленном выше решении автор многократно неверно использует логическую символику. В явном виде логические операции «конъюнкция» и «дизъюнкция» в школьном курсе математики не изучаются, не изучаются также законы формальной логики. В связи с этим, а также в связи с тем, что имеется верная последовательность всех шагов решения, работа оценена ненулевым баллом, однако, этот балл не максимальный.
4. Необходимым условием решения неравенств повышенной трудности является устойчивые умения тождественных преобразований выражений, в данном случае дробно-рациональных, показательных и логарифмических, а также умение оценить равносильность этих преобразований. Ошибки этого типа в 2015 году при решении задания 17, к сожалению, являются распространенными.
Таким образом, на основе анализа типичных ошибок в решениях задачи 17 участников ЕГЭ по математике в 2015 году можно констатировать следующее. Участники продемонстрировали различные методы решения неравенств предложенного типа, однако, при этом многие учащиеся получили за данную задачу нулевой балл. Многие из приступивших к решению задачи №17, очевидно, имеют не достаточно устойчивые навыки использования метода интервалов и метода введения вспомогательной переменной при решении неравенств, ошибаются при выполнении преобразований показательных выражений. Имеет смысл отрабатывать более тщательно применение метода введения вспомогательной переменной при решении неравенств, делая акцент на отличиях от уравнений, решаемых тем же способом. В частности, необходимо обращать внимание учащихся на то, что множество решений неравенства, полученного при введении вспомогательной переменной, целесообразно записать в виде одного или нескольких элементарных неравенств, в которых и возвращаться к исходной переменной. Запись же решений промежуточного неравенства в виде числовых промежутков часто не позволяет выпускникам продолжить решение.
На современном этапе развития образования единый государственный экзамен если и не является определяющим для выбора стратегии обучения, то на выбор тактики изучения отдельных тем школьного курса может влиять существенно.
Библиографическая ссылка
Кисельников И.В. ТИПИЧНЫЕ ОШИБКИ ПРИ РЕШЕНИИ ЗАДАНИЯ 17 УЧАСТНИКАМИ ЕГЭ ПО МАТЕМАТИКЕ ПРОФИЛЬНОГО УРОВНЯ В АЛТАЙСКОМ КРАЕ // Современные проблемы науки и образования. – 2016. – № 4. ;URL: https://science-education.ru/ru/article/view?id=24967 (дата обращения: 19.04.2024).