В настоящее время задача моделирования воздействия факторов окружающей среды на те или иные физиологические показатели животных зачастую оказывается достаточно сложной в силу принципиально нелинейного характера зависимостей. К числу таких сложных явлений можно отнести механизмы, реализующие процессы экзотрофии организмов на физиолого-биохимическом уровне, прежде всего с помощью организованных ансамблей пищеварительных ферментов [3]. Задача усложняется при исследовании адаптаций таких ферментных систем к действию различных экологических факторов [3; 4]. В основе таких адаптаций лежат три универсальных механизма: изменение типа молекул, изменение концентрации макромолекул и адаптивная регуляция функций макромолекул (Hochachka, Somero, 1973, цит. по [3]). Взаимодействие же таких механизмов в их конкретных проявлениях с учетом видовых особенностей, как правило, приводит к нелинейным эффектам, наблюдаемым в экспериментальной работе. В отечественной и зарубежной литературе представлено значительное количество методических подходов и базовых принципов, а также и конкретных алгоритмов для создания моделей, достаточно полно учитывающих и отражающих нелинейный характер исследуемых зависимостей и явлений [6; 9; 10]. Одним из достаточно перспективных методов, позволяющих создавать прогностические модели при достаточном объеме статистических данных поведения моделируемой системы, являются нейросетевые технологии [1; 6; 7]. Нейронные сети - весьма обширный класс моделей, в рамках которого выделяют несколько подтипов, объединяемых общностью архитектуры [2; 8]. Нейросетевой подход позволяет получить решение сразу в виде функции, удовлетворяющей требуемым условиям гладкости и, если нужно, обладающей заданным поведением на бесконечности. Важно отметить также устойчивость нейронных сетей по отношению к ошибкам в данных и естественное распараллеливание вычислений, что позволяет реализовать предлагаемые методы в случае сложной геометрии области, в которой ищется решение [1; 7].
Целью данного исследования является создание и анализ нейросетевой модели воздействия температуры инкубации на уровень активности щелочной фосфатазы белуги (Huso huso L.).
Материал и методы исследования
Объектами исследования служили годовики белуги, выращенные в искусственных условиях. Из слизистой оболочки, отделяемой от кишечника, с помощью специального скребка, с помощью раствора Рингера для холоднокровных животных готовился гомогенат в разведении 1:100. Все эксперименты проводились в условиях in vitro. Для исследования воздействия на фермент гомогенат и субстрат инкубировались в диапазоне температур от 0 до 60 °С. Уровень активности фермента определяли с использованием стандартных физиолого-биохимических методик [5].
Компьютерное моделирование осуществлялось с помощью математического пакета MATLAB 8.0.0, нейросетевые модели создавались с помощью расширения Neural Network Toolbox. Нейронная сеть определяется правилом построения (вид сети), числом элементов и способом их соединения друг с другом (структура сети) и коэффициентами, которые определяют конкретную функцию, моделирующую исследуемую зависимость (веса сети) [7]. Выбор вида сети, а также ее структуры и числе ее элементов в данном случае производился эмпирически с учетом доказанных сведений о том, что выбранная структура относится к классу универсальных аппрокиматоров [8]. Использовалась двуслойная сеть с одним скрытым слоем, содержащим 8 нейронов. Общая структура сформированной искусственной нейронной сети изображена на рис. 1.

Рис. 1. Структура сформированной нейронной сети
(Input – вход сети, Output – выходной слой искусственных нейронов и выходная переменная модели, Hidden – скрытый слой искусственной нейронной сети; цифрами обозначено количество переменных/нейронов в слое)
В качестве типа используемой архитектуры был выбран многослойный персептрон, а именно двухслойная сеть с одним скрытым слоем, в котором было размещено 7 нейронов.
Результаты и обсуждение
70% исходной выборки экспериментальных данных было зарезервировано для обучения сети, по 15% выделено для тестовой и контрольной выборок. Обучение искусственной нейронной сети производилось методом Левенберга-Марквардта. Ход обучения сформированной искусственной нейронной сети изображен на рисунке 2. Обучение заняло 7 циклов (эпох), ошибка обучения составила:
- для обучающей выборки – 6,66474*10-3;
- для контрольной выборки – 4,93819*10-3;
- для тестовой выборки – 3,76494*10-3.
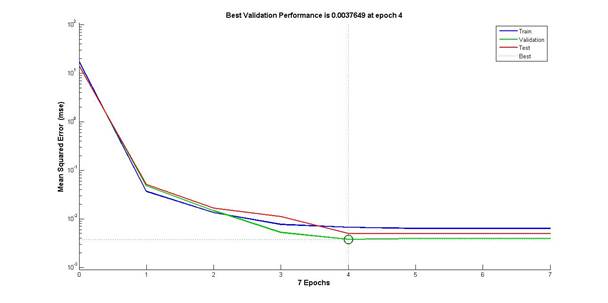
Рис. 2. Отображение хода обучения нейронной сети
(по горизонтали – количество эпох – циклов обучения, по вертикали – значения общей среднеквадратической ошибки для обучающей (train), контрольной (validation) и тестовой (test) выборок)
Результаты обучения модели в виде нелинейной зависимости изображены на рис. 3, где также отображены и точки, соответствующие исходным экспериментальным данным, формировавшим обучающую, тестовую либо контрольную выборки.
Из приведенного графика видно, что температурный оптимум для щелочной фосфатазы белуги находится в области свыше 50 °С. При этом в области оптимума, как и на большей части исследуемого температурного диапазона, кривая температурной зависимости имеет достаточно пологий характер, в силу чего, в частности, оптимум оказывается относительно «размытым». С учетом того что экспериментальное определение уровня активности в диапазоне от 50 до 70 °С проводилось с интервалом в 5 градусов, а не в 10, как в остальных случаях, данный эффект не может быть объяснен разреженностью точек измерения. Некоторое снижение уровня активности наблюдается при возрастании температуры свыше 65 °С, и на этом участке исследуемого диапазона температур относительно пологий характер функции сменяется существенно убывающим. Падение активности фермента при таком температурном воздействии часто наблюдается для пойкилотермных организмов и вызывается денатурирующим эффектом высокотемпературного воздействия.
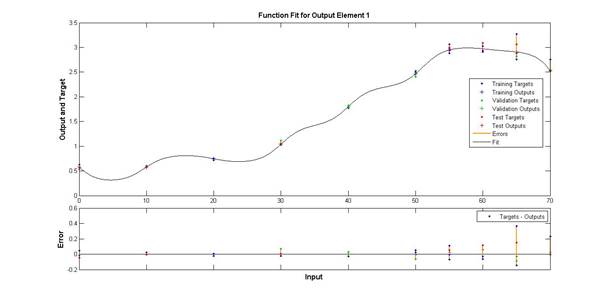
Рис. 3. Результаты обучения модели
(по горизонтали – значения температуры; по вертикали – на верхнем графике уровень активности исследуемого фермента: точками отмечены экспериментальные данные, линия – результат моделирования; на нижнем графике по вертикали – вычисленные значения ошибок)
Результат моделирования отражает значительную температурную лабильность исследуемого фермента, при этом верхний температурный диапазон (50-60 °С) оказывает существенное активирующее действие на уровень активности, это отличительная особенность данного пищеварительного фермента. Например, для ранее исследовавшейся температурной функции альфа-амилазы сибирского осетра и белуги, мальтазы белуги температуры данного диапазона оказывают угнетающее действие на активность фермента, скорее всего, как раз из-за проявляющегося в данном диапазоне денатурирующего эффекта в отношении ферментов.
Гистограмма распределения ошибок моделирования изображена на рис. 4, анализ данной гистограммы позволяет заключить, что в целом величины распределены достаточно равномерно и симметрично относительно нулевого уровня ошибок.
Для более детальной оценки качества обучения модели был проведен регрессионный анализ воспроизведенных данных в отношении к экспериментальным, результаты изображены на рис. 5.
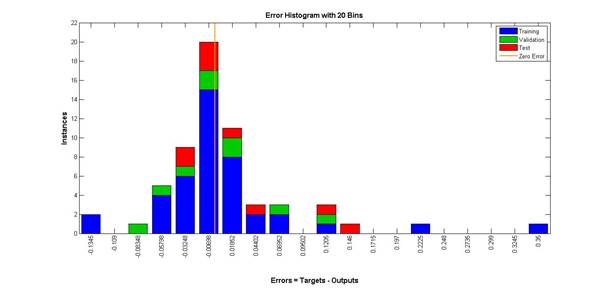
Рис. 4. Гистограмма распределения ошибок моделирования
(вертикальная линия соответствует нулевому значению погрешности)
Данные, полученные в ходе экспериментальных исследований, позиционировались при этом в качестве независимой переменной (Y), а результаты моделирования для тех же значений температуры – в качестве зависимой (X).
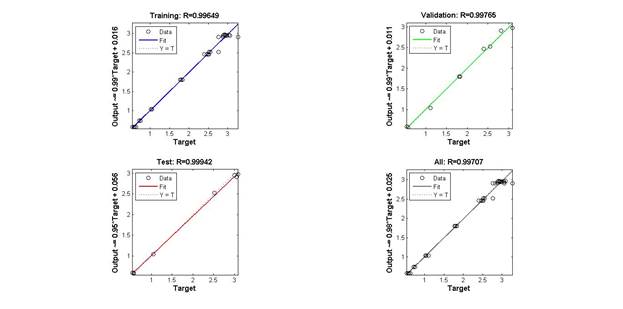
Рис. 5. Результат регрессионного анализа
(на каждом графике по горизонтали – экспериментальные данные, по вертикали – значения, полученные с помощью моделирования. Слева направо и сверху вниз изображены результаты для: обучающей выборки, контрольной выборки; общего объема выборки)
Уравнения регрессии и коэффициенты детерминации (R) для каждой из подвыборок данных и общего массива данных в целом выглядят следующим образом:
обучающая выборка: Y = 0.99X+0.016; R = 0.99649;
контрольная выборка: Y = 0.95X+0.056; R = 0.99942;
тестовая выборка: Y = 0.99X+0.011; R = 0.99765;
общий массив данных: Y = 0.98X+0.025: R = 0.99707.
Проведенный анализ подтверждает достаточно хорошее качество обучения созданной искусственной нейронной сети с учетом ограниченного объема используемой для обучения выборки. Данный показатель свидетельствует, с одной стороны, о достаточно хорошем качестве обучения, а с другой - сопоставление значений ошибки для обучающей, тестовой контрольной выборок позволяет сделать вывод об отсутствии эффекта переобучения.
Выводы:
1. Методология искусственных нейронных сетей достаточно хорошо применима при решении задач экологической физиологии пищеварения рыб. Искусственные нейронные сети уже достаточно широко применяются в биологических и экологических исследованиях, и, по-нашему мнению, с учетом полученных ранее результатов в области моделирования и многомерного статистического анализа целесообразно расширить спектр их применений и для задач экзотрофии рыб.
2. Непосредственно рассматриваемая в работе модель была создана на относительно небольшой выборке данных, что заставило использовать ряд дополнительных методов оценки ее качества. Достигнутая точность моделирования при этом позволяет сделать вывод о существенной ценности модели как средства прогноза уровня активности пищеварительного фермента при температурном воздействии.
3. С учетом сказанного выше необходимо отметить, что рассматриваемая методика по своей сути является одним из вариантов построения нелинейной регрессии. Созданную модель и результаты ее работы целесообразно в дальнейшем использовать в качестве компонента более сложных моделирующих систем, отражающих не только особенности поведения, но и структурные особенности моделируемых механизмов мембранного пищеварения.
4. Характерной особенностью температурного оптимума щелочной фосфатазы белуги является его локализация в области высоких значений температур (существенно выше физиологических значений, близких к величинам, при которых начинает проявляться денатурирующий эффект).
Библиографическая ссылка
Мартьянов А.С., Бедняков Д.А., Неваленный А.Н. МОДЕЛИРОВАНИЕ ВОЗДЕЙСТВИЯ ТЕМПЕРАТУРЫ ИНКУБАЦИИ НА УРОВЕНЬ АКТИВНОСТИ ЩЕЛОЧНОЙ ФОСФАТАЗЫ СЛИЗИСТОЙ ОБОЛОЧКИ КИШЕЧНИКА БЕЛУГИ (Huso huso) С ПОМОЩЬЮ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ // Современные проблемы науки и образования. 2016. № 3. ;URL: https://science-education.ru/ru/article/view?id=24690 (дата обращения: 16.02.2026).



