Математические дисциплины входят в состав образовательных программ подавляющего большинства направлений подготовки бакалавров и специалистов. Кроме того, в настоящее время значительно расширился круг лиц, получающих высшее образование. Поэтому возникает необходимость рассмотрения проблем, связанных с оптимизацией учебного процесса по математическим дисциплинам. В данной работе мы остановимся на проблеме актуализации знаний студентов по математике, являющейся, на наш взгляд, краеугольной точкой математического образования в вузе.
Применительно к учебному процессу, на наш взгляд, можно понимать актуализацию как «извлечение усвоенного материала из долговременной или кратковременной памяти с целью последующего использования его при узнавании, припоминании, воспоминании или непосредственном воспроизведении» [4].
В настоящее время объективно существует проблема ухудшения качества освоения большинством обучающихся нового материала по математике. В той или иной мере это проявляется по-разному: недостаточный уровень сформированности понятийного аппарата (форма и объем понятий) и, как следствие, значительные затруднения в выявлении понятийных отношений (использование одних понятий для раскрытия содержания новых, решение задач и освоение способов их решения и т.д.). Причины указанных затруднений могут быть разными. Для студентов, освоивших материал средней школы лишь на уровне воспроизведения понятий и приемов решения простейших математических задач, характерны трудности в освоении способов мыслительной деятельности (анализ, синтез). Здесь же можно отметить слабую сформированность умений, способствующих учебной деятельности во всех ее видах. Для более подготовленных студентов основной причиной снижения качества освоения нового математического аппарата можно указать недостаток времени на освоение этого аппарата. Особенно это проявляется на второй год обучения, когда количество аудиторных часов уменьшается и, как следствие, это ведет еще и к тому, что увеличивается временной разрыв между ранее освоенными знаниями и знаниями, изучаемыми в данный момент.
Следствием указанных причин является то, что при изучении новых естественнонаучных и математических понятий преподавателю приходится сталкиваться с проблемой представления и изложения нового материала так, чтобы, с одной стороны, освоение происходило на необходимом уровне сложности, а с другой стороны, новые понятия были изложены на научном языке, с использованием достаточно четких научных определений.
Одним из способов решения этой проблемы является актуализация знаний, которую можно реализовать в виде:
– актуализации собственно имеющихся математических знаний;
– актуализацию имеющегося практического опыта, не обязательно связанного с естественнонаучными понятиями.
В связи с вышеизложенным возникает необходимость корректировки содержания курса математики. Такой вывод прослеживается во многих исследованиях, рассматривающих различные аспекты учебного процесса по математике в вузе [2, 5 и др.]. В частности, отмечается, что «изложение курса математики … постоянно разрывается различными по своим идеологическим установкам и объему учебного времени содержательными блоками, имеющими, как правило, изолированные области функциональной применимости…» [2]. Традиционные фундаментальные разделы математики как учебной дисциплины – это алгебра, геометрия и математический анализ. Опыт показывает, что последовательность изложения этих разделов не оказывает существенного влияния на качество освоения математических знаний. Изучение курса высшей математики можно начинать с алгебры или геометрии, можно начинать с математического анализа. Однако конкретная учебная ситуация может существенно повлиять на порядок построения тем внутри фундаментального раздела.
Возьмем, для примера, раздел «Математический анализ». Этот раздел включает ряд подразделов: пределы, производные, интегралы, дифференциальные уравнения, ряды, функции нескольких переменных. С логико-математической точки зрения указанные подразделы можно изучать в той последовательности, в какой они приведены выше: все необходимые факты к нужному моменту уже будут установлены. Однако логика научного познания не всегда тождественна логике дидактики. Логика дидактики реального учебного процесса должна учитывать проблемы, возникающие в ходе изучения студентами курса математики. В реальности обучающиеся склонны забывать материал. С логико-математической точки зрения такое невозможно: если что-то ранее доказано, значит это уже известно, и в любой момент может быть использовано. Однако если студенты фактически забыли какие-то понятия, теоремы или формулы, то в данный нужный момент возникает ситуация «неизвестности», «незнания», и объективно логически безупречные построения становятся субъективно непонятными и недоступными. Например, введение частных производных много позже обычных производных, как показывает опыт, приводит к значительным трудностям: забываются правила и формулы дифференцирования, а часто – и сам смысл производной как скорости изменения функции. В результате задания типа «найти частную производную по переменной x выражений y2sin x; 3y3 + x» и т.п. ставят значительную часть студентов в тупик. Приходится объяснять, что частная производная – это, прежде всего, производная, и для ее вычисления никакие дополнительные формулы не нужны. Таким образом, следует признать, что удаленное расположение тем «Производные» и «Частные производные» вызывает необходимость актуализации значительного числа важнейших не так давно ранее изученных понятий и фактов. Зачастую приходится практически заново рассказывать тему «Производные». Актуализация математических знаний в ходе изучения курса неизбежна, это часть дидактического процесса. Но когда актуализация вынужденно подменяется повторным изложением, это недопустимо.
Как избежать столь «крайней» ситуации? Поскольку актуализация, как важный методический фактор неизбежна, следует заранее планировать в содержании специальные «актуализационные» элементы – дидактические связки между сопряженными темами. В частности, следует тщательно подбирать примеры.
Пример 1. Дана функция: f (x) = a2 sin x, где a – некоторая константа. Найти f′(x).
Наличие в памяти такого рода примеров позволяет, как показывает опыт, гораздо эффективнее работать с понятием «частная производная». Можно пойти и по другому пути – попробовать «сблизить» темы: после изучения производной ввести понятие частной производной, при этом подраздел «Функции нескольких переменных» частично может быть изложен позднее (например, после интегралов).
Приведем еще пример дидактических затруднений, вызванных забыванием. Подраздел «Ряды» очень существенно опирается на подраздел «Пределы». Но временной интервал между этими дидактическими единицами обычно бывает значительным. Мы провели эксперимент: рассмотрели числовые ряды непосредственно после предела последовательности. Заметим, что почти все признаки сходимости (кроме интегрального) основаны исключительно на свойствах пределов. Эксперимент показал, что задачи на исследование сходимости числовых рядов решаются значительно успешнее, чем при традиционном изложении. Пределы числовых последовательностей и суммы рядов – понятия сопряженные, очень важные для понимания сути бесконечности как математической абстракции. И рассмотрение этих вопросов «в одном пакете» дидактически вполне целесообразно. Что касается степенных и тригонометрических рядов, то эти темы можно рассмотреть позднее, т.к. дидактическая связка в виде числовых рядов уже построена.
На наш взгляд, отсутствие дидактически связующих элементов в сопряженных темах является основной причиной полного «забывания» материала.
Пример 2. Важнейшее понятие «экстремум» разбивается, а точнее сказать – разрывается на части: экстремум функции одной переменной, экстремум функции двух переменных и т.д. Сначала определяют экстремум функции одной переменной f (x) и дают достаточные условия:
![]() меняет знак в точке x0. (1)
меняет знак в точке x0. (1)
Затем «линия экстремумов» прерывается и возникает при рассмотрении второй производной:
![]() . (2)
. (2)
Спустя еще немало времени, определяют условия экстремума функции двух переменных:
![]() ;
; ![]() . (3)
. (3)
Далее рассматривается экстремум функции трех и более переменных, условия усложняются. Вместо содержательно-методической линии «Экстремумы» имеем набор отрезков. При таком изложении очень трудно актуализировать знания, нет стержневой идеи, только отдельные факты. Именно так студенты воспринимают экстремумы, не видя связи между экстремумами функции одной переменной, экстремумами функции двух переменных и т.д., между условиями (1), (2) и (3), тем более что из-за нехватки времени доказательства часто опускаются. Какова общая идея условий экстремума? Она следующая. Разность f (M) – f (M0) в окрестности точки экстремума имеет постоянный знак. Скажем, f (M) – f (M0) > 0 для минимума. Эта разность представляется так:
![]() . (4)
. (4)
При условии d f (M0) = 0 знак разности (4) определяется знаком второго дифференциала d 2f (M0). Вот это – основное. Остальное – технические вопросы. Условие d f (M0) = 0 означает grad f (M0) = 0, т.е. fx′(M0) = 0, fy′(M0) = 0, … для функции двух и более переменных; (по аналогии с f ′(x0) = 0 для функции одной переменной). Условие d 2f (M0) > 0 означает положительную определенность матрицы Гессе, состоящей из значений вторых производных, для случая двух и более переменных и положительность значения второй производной для случая одной переменной.
Приведенные рассуждения принципиально важны и обязательно должны быть доведены до студентов. Иначе, при фрагментарном изложении материал быстро забудется. Заметим, что условия (1) также вписываются в приведенную схему, но лишь для функции одной переменной. Аналогов им для функций двух и более переменных нет.
Пример 3. Кроме общей идеи, на практике весьма важны конкретные детали представления учебного материала. Поясним это на примере изложения вопросов, касающихся экстремума, монотонности, перегиба, выпуклости и графиков функции одной переменной.
Рассмотрим пример учебной ситуации, иллюстрирующий не только приемы актуализации имеющихся естественнонаучных знаний и практического опыта, но и позволяющей корректировать построение содержательно-методической линии изучаемого материала в пределах одного раздела.
При изучении темы «Экстремумы функции» наряду с первым достаточным признаком экстремума: равенство нулю производной в точке экстремума f ' (x0) = 0 и смена знака производной при переходе через точку экстремума, который часто позиционируется как основной, рассматривается второй достаточный признак экстремума функции.
Приведем стандартную формулировку этого признака: «Если в точке х0 первая производная функции f (x) равна нулю (f ' (x0) = 0), а вторая производная в этой точке существует и отлична от нуля (f ''(x0) ≠ 0), то при f ''(x0) < 0 в точке х0 функция имеет максимум, и минимум – при f ''(x0) > 0» [3, с. 205]. Обычно второй достаточный признак рассматривается сразу же после первого достаточного признака, как дополнительный [1, 3, и др.], и доказательство, если позволяет учебное время, приводится в формальном аналитическом виде, или опускается полностью в случае дефицита времени. Это приводит к естественным трудностям в понимании данного материала у студентов, ранее освоивших первый достаточный признак. В частности, обучающиеся часто допускают ошибку в соответствии знака второй производной и характера экстремума. Например, в точке максимума обучающиеся ошибочно определяют знак второй производной положительным: f ''(x0) > 0, поскольку интуитивно понятие максимума ассоциируется с признаком возрастания функции на интервале (f ' (x) > 0). Аналогичная ошибка допускается и для минимума функции, когда существенный признак убывания функции – отрицательное значение первой производной на интервале (f ' (x) < 0), ассоциативно переносится на условие минимума во втором достаточном признаке: f ''(x0) < 0.
Обратим внимание на то, что подобная ситуация имеет место и при изучении следующей темы «Выпуклость графика функции. Точки перегиба», что приводит к ошибке в определении характера выпуклости графика функции. В частности, положительный знак второй производной на некотором интервале, где f ''(x) > 0, обучающиеся «интуитивно» связывают с выпуклостью вверх и наоборот, отрицательное значение второй производной f ''(x0) < 0 – с выпуклостью вниз.
В дальнейшем большинство обучающихся, осознав факт ошибки, механически запоминают формулировку второго достаточного признака, но при этом все же стараются избегать его применения. В результате такого формального заучивания, спустя некоторое время, условия второго достаточного признака забываются.
Казалось бы, можно ограничиться первым достаточным признаком экстремума, который обучающиеся осваивают вполне качественно, поскольку впервые знакомятся с ним в курсе математики средней школы. Однако впоследствии формальное освоение условий второго достаточного признака экстремума функции одной переменной ведет к трудностям в понимании достаточного признака экстремума функции двух переменных, который определяется через частные производные второго порядка.
На наш взгляд, можно эффективно раскрыть понятийное содержание, исключить смешение существенных признаков в рассмотренных примерах и обеспечить осознанное качественное освоение как условий экстремума функции во втором достаточном признаке, так и условий, определяющих характер выпуклости графика функции, актуализируя имеющиеся математические и естественнонаучные понятия и факты, а также практический опыт, не обязательно напрямую связанный с ними.
Прежде всего, это наглядное представление графика дифференцированной функции, а именно характера его выпуклости в окрестности точки экстремума: в случае максимума выпуклость графика функции направлена вверх и, соответственно, в случае минимума – вниз.
Заметим, что понятие производной и ее геометрическая интерпретация как тангенса угла наклона касательной к графику функции в некоторой точке, изучаются еще в курсе средней школы, поэтому можно принять, что имеющиеся математические знания позволяют обучающемуся судить о горизонтальном положении касательной к графику функции в точке экстремума (tg α = 0, где α – угол наклона касательной по отношению к горизонтальной оси координат) (рис. 1).

Кроме того, обучающимся безусловно знакомо естественнонаучное понятие ускорения и его математическая аналогия в виде второй производной координаты (переменной х) по времени. Здесь можно отметить, что собственный практический опыт и имеющееся представление обучающегося о том, что ускорение имеет отрицательное значение при уменьшении скорости, позволяет вполне качественно сформировать смысловую взаимосвязь: при въезде в гору скорость движения тела уменьшается, следовательно, ускорение, а потому и вторая производная координаты по времени имеет отрицательный знак и, наоборот – положительное ускорение (вторая производная – положительна), можно ассоциировать со спуском в ложбину, сопровождающимся увеличением скорости (рис. 2).

Актуализация перечисленных фактов, как показывает опыт, позволяет достаточно успешно решать методическую задачу качественного освоения обучающимися как техники определения характера выпуклости, так и условий второго достаточного признака экстремума. Содержание и порядок методической работы преподавателя, на наш взгляд, представляется следующим – первоначально необходимо подвести обучающихся к мысли о том, что в точке экстремума функции, например, максимума, выполняются два условия – график функции должен иметь выпуклость вверх, и при этом касательная к графику должна быть расположена горизонтально (параллельно оси Ох). В соответствии с рассмотренными ранее примерами первое условие определяется отрицательным знаком второй производной, а второе – равенством нулю первой производной (рис. 3).
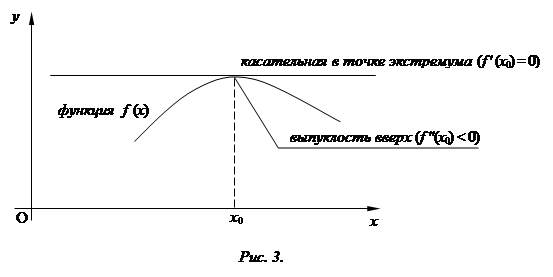
Описанные приемы различного рода актуализации имеющегося как учебного, так и субъективного опыта, позволяют обоснованно выстроить содержательно-методическую линию изучения раздела «Исследование функции. Построение графиков». В наиболее продуктивном варианте это обеспечивает освоение условий, определяющих выпуклость графика, а затем, на основе имеющихся геометрических интерпретаций производной и необходимого признака экстремума, формирование правильного понимания второго достаточного признака экстремума функции.
Библиографическая ссылка
Боярский М.Д., Гниломедов П.И. АКТУАЛИЗАЦИЯ ЗНАНИЙ СТУДЕНТОВ КАК ФАКТОР ИЗМЕНЕНИЯ СТРУКТУРЫ И СОДЕРЖАНИЯ КУРСА МАТЕМАТИКИ // Современные проблемы науки и образования. 2016. № 3. ;URL: https://science-education.ru/ru/article/view?id=24668 (дата обращения: 16.02.2026).



