В настоящее время информатика один из немногих инновационных и востребованных предметов, делающих школу современной, приближенной к жизни и запросам общества [1,2].
Ни компьютер, ни информационные технологии сами по себе не способны сформировать у выпускников присущие им качества, они являются лишь вспомогательными средствами решения мировоззренческих задач, а найти эти решения учащийся может лишь с помощью грамотного, творчески работающего учителя [4,5].
Задачей учителя на уроках информатики является формирование у учащихся информационной компетентности – одного из основных приоритетов в современном общем образовании, который носит общеучебный и общеинтеллектуальный характер.
При использовании традиционной методики преподавания вся нагрузка ложится на учителя, нагрузка учащихся минимальна в плане учебной деятельности. Приходится искать более новые методы, средства, более совершенную, чем традиционная методика преподавания, какую-либо из развивающих, личностно-ориентированных технологий обучения, технологий на основе активизации учебной деятельности учащихся. Одна из таких технологий обучения – это проблемное обучение.
Проблемное обучение является результатом достижения передовой практики и теории обучения и воспитания, сочетается с традиционным типом обучения, является общепризнанным эффективным средством общего и интеллектуального развития учащихся.
В наши дни под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную деятельность учащихся по их разрешению, в результате чего и происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие мыслительных способностей.
В основе концепции проблемного обучения положена теория мышления, как продуктивного процесса. В современной России в условиях относительной либерализации системы образования получили возможность своего развития и воплощения на практике различные педагогические технологии, концепции и методы обучения. Часть из них пришла из западной системы образования (нейролингвистическое программирование, гештальттехнологии и др.), часть – соответствует сравнительно старым российским идеям в области образования (например, основы концепции свободного воспитания были заложены Л.Н. Толстым, а педагогики сотрудничества – еще К.Д. Ушинским) или сравнительно новым концепциям, разработанным или доработанным советскими и современными российскими учеными (концепция развивающего обучения Д.Б. Эльконина и В.В. Давыдова, гуманно-личностная технология Ш.А. Амонашвили, обогащающая модель обучения Э.Г. Гельфмана и М.А. Холодной, технология укрупнения дидактических единиц П.М. Эрдниева и Б.П. Эрдниева и мн. др.).
Сущность проблемного обучения заключается в том, что учитель не просто сообщает конечные выводы науки, а делает учащихся как бы участниками научного поиска: поставив вопрос, он вскрывает внутренние противоречия, возникающие при его решении; рассуждая вслух, высказывает предположения, обсуждает их, опровергает возможные возражения, доказывает истину.
В основе проблемного обучение положено создание особого вида мотивации – проблемной. Поэтому технология требует адекватного конструирования дидактического содержания материала, который должен предсталяться как цепь проблемных ситуаций.
Сама логика научных знаний в генезисе представляет логику проблемных ситуаций. Проблемные ситуации могут быть различными по содержанию неизвестного, по уровню проблемности, по виду рассогласования информации, по другим методическим особенностям (табл. 1).
Таблица 1
|
Основание классификации |
Виды |
|
по содержанию неизвестного |
|
|
По уровню проблемности |
|
|
По виду рассогласования информации |
|
|
По методическим особенностям |
|
Источником педагогической проблемной ситуации являются активизирующие действия, вопросы учителя, подчеркивающие новизну, важность, красоту и другие отличительные качества объекта познания. Но при этом само создание психологической проблемной ситуации сугубо индивидуально. Познавательная задача должна быть ни слишком трудной, ни слишком легкой, иначе она не создаст проблемной ситуации для учеников. Проблемные ситуации могут создаваться на всех этапах процесса обучения: при объяснении, закреплении, контроле.
На рисунке представлена технологическая схема проблемного обучения (постановка и разрешение проблемной ситуации) (рис. 1).
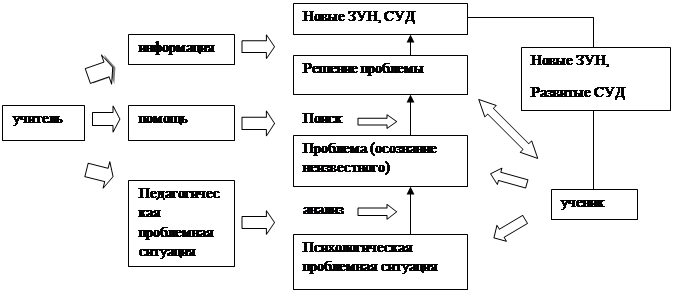
Рис. 1. Технологическая схема проблемного обучения
Для реализации проблемной технологии необходимо выполнение следующих действий:
1. Выполнение отбора самых актуальных, сущностных задач;
2. Определение особенностей проблемного обучения в различных видах учебной работы;
3. Выполнение построения оптимальной системы проблемного обучения, создание учебных и методических пособий и руководств;
4. Использование личностного подхода и мастерства учителя, способные вызвать активную познавательную деятельность ребенка.
В качестве примера использования проблемно-поискового метода можно предложить рассмотрение сложного условия при изучении оператора ветвления на теме «Оператор ветвления» [1].
Задача. Найти наибольшее число из трех заданных чисел. На доске записываю несколько троек чисел: 568, 742, 390.
Учащиеся называют максимальное число: 742.
Вопрос: Каким образом вы определили, что данное число максимальное?
Если это первые уроки программирования, то учащиеся затрудняются ответить на этот вопрос, поскольку они еще не привыкли отслеживать свои действия при решении задач. Надо помочь дополнительными вопросами, в поисках верного ответа:
Учитель: А как на уроке математике вы бы сравнили натуральные трехзначные числа?
Ответ: Посмотрели разряд числа – если единицы разрядов сотен равны, то сравниваем единицы разрядов десятков, если они равны, сравниваем разряд единиц и больше то число, у которого разряд сотен больше.
Вывод: Итак, максимальное число: 742.
Проблема: А как компьютер сравнит три числа? Машина может сравнивать только два числа
Обозначим одно число буквой А, второе число буквой B, третье число – буквой С.
Учащиеся: Предлагают такой вариант решения проблемы: надо сравнивать первые два числа, а затем, большее из них с третьим числом.
Учитель: Нарисуйте в тетради блок-схему для сравнения трех чисел.
Учащиеся в тетради рисуют блок-схему, а затем сравнивают составленную ими схему с блок-схемой на доске. Одному из учащихся предлагаю сделать анализ блок-схемы. А теперь в соответствии с блок-схемой составьте программу.
Учащиеся самостоятельно составляют программу.
Учитель: Проверьте правильность работы программы, введите заданные числа и посмотрите результат.
Проблема: А может ли измениться исходное значение переменной А в процессе работы программы?
Ответ: Да.
Учитель: А как? Ответ обоснуйте.
Решение:
1. Находим наибольшее из первых двух данных чисел A и B, а затем – максимальное из полученного числа и третьего данного числа С.
Program MAX1;
Var A, B, C, max: real;
Begin
writeln (‘Введите три числа A, B, C’);
readln (A, B, С)
if A>B then max:=A else max:=b;
if C > max then max:=C;
writeln (‘Максимальное значение=’,max);
end.
Учитель: Как вы думаете, можно ли решить задачу другими способами?
Учащиеся получают задание на уроке и продолжают поиск решения задачи.
Предполагаемые решения учащихся:
2 способ. При решении задачи можно проверить, является ли первое число A максимальным и если не является, то сравниваем второе и третье число B и C.
Program MAX2;
Var A, B, C, max: real;
Begin
writeln (‘Введите три числа A, B, C’);
readln (A, B, С);
If (A>B) and (A>C) then max:=A;
if B>C then Max:=B else Max :=C;
Writeln(‘Максимальное значение =’, Max);
End.
Также создаётся ситуация предположения, которая основана на возможности выдвинуть собственную версию. Например, при изучении темы «Системы счисления» учащимся предлагается сравнить числа, записанные в позиционной и непозиционной системах счисления (эти термины в начале урока не называются).
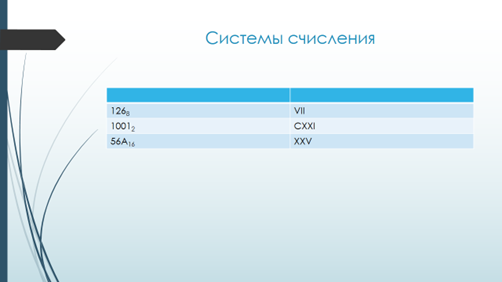
Рис.2. Работа с системами счисления
Затем знаки, используемые при записи чисел, меняются местами, и учащиеся пытаются объяснить, почему в одном случае это не повлияло на значение числа, а в другом случае повлияло. Делая вывод, что иногда при записи числа место цифры (или позиция) имеет значение, учащихся самостоятельно формулируют тему «Позиционные и непозиционные системы счисления».
Этапы построения проблемного занятия по информатике и ИКТ могут быть следующими:
– актуализация опорных знаний;
– анализ проблемного задания;
– вычленение проблемы;
– выдвижение всевозможных предположений;
– сужение поля поиска;
– доказательство рабочих гипотез;
– проверка правильности решения.
Первый, второй и третий этапы соотносятся с организацией проблемной ситуации; четвертый и пятый – с выдвижением гипотезы; шестой – с доказательством, седьмой – с выводом.
Результативность использования проблемного обучения на уроках информатики можно оценить с помощью критериев:
1. Наличие у ученика положительного мотива к деятельности в проблемной ситуации («Хочу разобраться, хочу попробовать свои силы, хочу убедиться смогу ли разрешить эту ситуацию...»);
2. Наличие у учащихся положительных изменений в эмоционально — волевой сфере («Испытываю радость, удовольствие от деятельности, мне это интересно, могу с усилием воли концентрировать свое внимание...»);
3. Переживание учащимися субъективного открытия («Я сам получил этот результат, я сам справился с этой проблемой, я вывел закон»);
4. Осознание учеником усвоения нового как личностной ценности («Лично мне это нужно, мне важно научиться решать эти ситуации, мне будут эти знания нужны»);
5. Овладение обобщенным способом подхода к решению проблемных ситуаций: анализом фактов, выдвижением гипотез для их объяснения, проверкой их правильности и получением результата деятельности.
Библиографическая ссылка
Акимова И.В., Губанова О.М., Пудовкина Ю.Н. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭЛЕМЕНТОВ ПРОБЛЕМНОГО ОБУЧЕНИЯ НА УРОКАХ ИНФОРМАТИКИ И ИКТ В ШКОЛЕ // Современные проблемы науки и образования. 2016. № 3. ;URL: https://science-education.ru/ru/article/view?id=24642 (дата обращения: 16.02.2026).



