Динамические рабочие листы – это интерактивные электронные образовательные ресурсы. Они создаются средствами систем динамической математики (GeoGebra, 1C: Математический конструктор, The Geometer’s Sketchpad и т.п.>). Сегодня эти средства обучения становятся все более популярными. Они используются для изучения самых разных разделов математики в школе и вузе: геометрии, алгебры, математического анализа, математической статистики и теории вероятностей. Коллекции динамических листов, созданных для этих целей, можно найти в блогах учителей, на официальных сайтах ассоциаций учителей и преподавателей математики, компьютерных компаний [2,3,4,7,8]. Популярность этих средств обучения объясняется тем, что они открывают дорогу экспериментальным методам в математике, позволяют визуализировать динамику работы с образами математических объектов, могут быть сделаны самими учащимися.
Планируемое включение в систему общего математического образования России элементов финансовой математики [5] ставит вопрос о возможностях использования этих средств для поддержки решения задач с экономическим содержанием.
В данной статье мы представляем методику обучения учащихся через задачи [6]. Главной ее особенностью является то, что изучаемые математические факты выступают не основой, а результатом работы с задачей. К их обнаружению учащихся подводят компьютерные эксперименты, а также симуляция финансовых операций с использованием рабочих динамических листов.
Уровень подготовки выпускников общеобразовательных школ к решению задач на погашение кредитов по итогам ЕГЭ 2015 года в Архангельской области
В Единый государственный экзамен по математике в 2015 году впервые была включена задача экономического содержания. Ее назначение – проверка готовности выпускников общеобразовательных школ к практическому применению математических методов. Усилить практико-ориентированный характер диагностической задачи решили за счет использования в качестве ее сюжетного плана ситуации, связанной с погашением кредита. Разработчики ЕГЭ, видимо, полагали, что кредитный процесс интуитивно понятен учащимся из практики формирования семейного бюджета. Однако, как показал анализ результатов решения этой задачи выпускниками школ Архангельской области, эти предположения не оправдались.
В прошедшем году на основной этап экзамена была вынесена следующая задача на кредиты: «15 января планируется взять кредит в банке на 14 месяцев. Условия его возврата таковы: 1 числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; со 2 по 14 число каждого месяца необходимо выплатить часть долга; 15 числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 15 % больше суммы, взятой в кредит. Найдите r». К ее решению приступило 3446 выпускников 11 классов, сдававших экзамен в Архангельской области. Из них только 35 человек справились с ней и получили максимальное количество баллов. 95,56 % учеников, приступивших к решению задачи, получили за ее решение 0 баллов. Самым трудным для учащихся оказался этап построения математической модели задачной ситуации. Несмотря на то, что в условии задачи график погашения кредита был описан достаточно подробно, выпускники не смогли правильно записать выражения для ежемесячных выплат, начислений на остаток долга; затруднились выразить сумму выплат через величину кредитного займа. Самыми распространенными ошибками были: нарушение порядка последовательностей начислений и выплат по кредиту, допущение постоянства размеров ежемесячных выплат, начисление процентов не на остаток долга, а на размер займа.
Все это свидетельствует о том, что учащиеся плохо представляют себе процесс кредитования, несмотря на то, что услугами кредитных организаций пользуется большинство семей.
Использование рабочих динамических листов при изучении через задачи особенностей аннуитетного графика погашения кредита
Наиболее часто банки предлагают потребителям график погашения кредита, при котором ежемесячные (ежегодные) выплаты остаются неизменными на всем протяжении срока (теоретические основы с учетом предлагаемых банками вариантов подробно описаны нами в [1, с. 77-82]). Такой график называется аннуитетным, а сам ежемесячный (ежегодный) платеж аннуитетом (от французского слова annuité – ежегодная рента). Банки, предлагая различные варианты аннуитетных графиков погашения кредита, предоставляют заемщику право выбора срока его предоставления. Как грамотно воспользоваться этим правом? Как минимизировать переплаты по кредиту, не испытывая дискомфорта от дополнительной финансовой нагрузки? Как избежать неприятных ситуаций при досрочном погашении кредита? Ответы на эти вопросы должны получить учащиеся в ходе решения задач на погашение займов.
Первая задача подбирается таким образом, чтобы представить учащимся механизм расчетов по кредиту, а также мотивировать необходимость вывода формул расчета аннуитета и суммы переплат.
Задача 1. Николай хочет взять в кредит 1,4 млн рублей под 10 % годовых с аннуитетным графиком погашения займа. Составьте для него план погашения кредита, если Николай просит, чтобы сумма ежегодных выплат не превышала 330 тыс. рублей, а сумма переплаты по кредиту была наименьшей.
|
Год, № |
Остаток долга, тыс. руб. |
Ежегодная выплата, тыс. руб. |
Как было показано ранее, наиболее типичной ошибкой учащихся является неверное определение суммы, на которую начисляется процент по кредиту. Проведенный нами в ходе апробации предлагаемой методики опрос показал, что одни учащиеся полагают, что процент начисляется сразу на всю сумму займа в момент предоставления кредита; другие – что начисление происходит на остаток долга после проведения каждого транша. Предотвратить появление этих ошибок позволяет использование рабочего динамического листа (рис. 1) в качестве средства поддержки решения задачи. Он создан таким образом, что переход к каждому следующему году автоматически увеличивает сумму долга в соответствии с избранным значением ставки по кредиту (p, %). Транш выполняется вручную (перемещением «ползунков»), причем его размер определен установленным размером аннуитетного платежа (даже в момент последней выплаты).
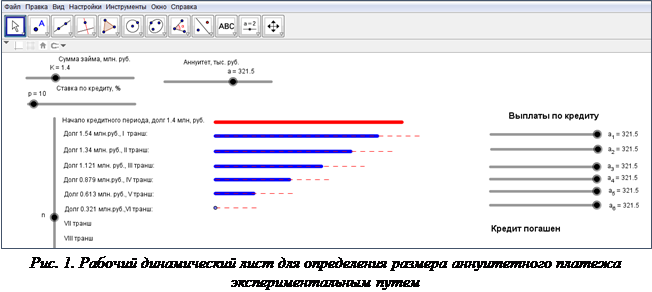
Этот ресурс позволяет учащимся подобрать такой аннуитет (a, у.е.), чтобы сумма долга перед последним траншем, с одной стороны, не превышала его, а с другой – была максимально приближена к нему. При этом остальные требования задачи должны быть удовлетворены. План погашения кредита, полученный в результате экспериментального решения задачи, представлен на рис. 1. Сложность подбора подходящей величины аннуитета создает мотив для обращения к аналитическим методам.
Аналитическое решение задачи требует вывода формулы, позволяющей выражать величину аннуитетного платежа (а, у.е.) через величину займа (К, у.е.), годовую процентную ставку по кредиту (p, %) и срок реализации аннуитетного графика погашения кредита (n, лет). Работа с динамическим чертежом в достаточной мере готовит учащихся к самостоятельному выводу этой формулы в ходе решения второй задачи серии.
Задача 2. Выведите формулу для вычисления размера аннуитетного платежа в зависимости от величины займа (К, у.е.), ежемесячной процентной ставки по кредиту (p, %) и срока его предоставления (n, лет).
Так, опираясь на созданный моделью образ, учащиеся безошибочно описывают процесс погашения кредита в течение n лет как последовательность величин:
![]()
![]() (
(![]()
![]() (
(![]()
…
![]() .
.
Они также способны представить в виде неравенства (1) вывод о том, что кредит будет погашен в тот год, когда после начисления процентов остаток по кредиту не будет превышать аннуитета:
![]() (1)
(1)
Условие минимизации переплаты по кредиту приводит их к уравнению:
![]() (2)
(2)
Решение уравнения (2) с применением формулы разности степеней приводит к желаемой формуле:
![]()
(3)
Применение формулы (3) к задаче 1 позволяет учащимся получить выражение для уточнения экспериментального результата:
![]() (млн руб.)=321,45 тыс. руб.
(млн руб.)=321,45 тыс. руб.
Для концентрации внимания учащихся на главной особенности аннуитетного графика погашения кредита может быть предложена дополнительная задача.
Задача 3. Определите, какова будет наименьшая сумма переплаты по кредиту в задаче 1.
При решении этой задачи учащиеся вербализируют представленный динамической моделью факт о том, что аннуитетный график погашения кредита предполагает внесение равных сумм через равные промежутки времени, а потому сумма переплаты по кредиту может быть рассчитана по формуле:
![]() (4)
(4)
Ее применение приводит к выводу, что ![]() (тыс. руб.).
(тыс. руб.).
Постановка следующей задачи обеспечивает учащимся возможность получения дополнительных сведений об особенностях аннуитетного графика погашения кредита.
Задача 4. Илья взял кредит в размере 1,5 млн рублей под 10 % годовых с аннуитетным платежом 250 тыс. руб. в год. Составьте для него план погашения кредита. Детализируйте в плане, какую долю в ежегодной выплате составляет выплата основного долга, какую долю составляет оплата процентов по кредиту. Выделите период, в который оплата по процентам превышает оплату основного долга.
|
Год, № |
Остаток долга, тыс. руб. |
Ежегодная выплата и ее состав |
||
|
Ежегодная выплата, тыс. руб. |
Оплата основного долга, % |
Оплата процентов, % |
||
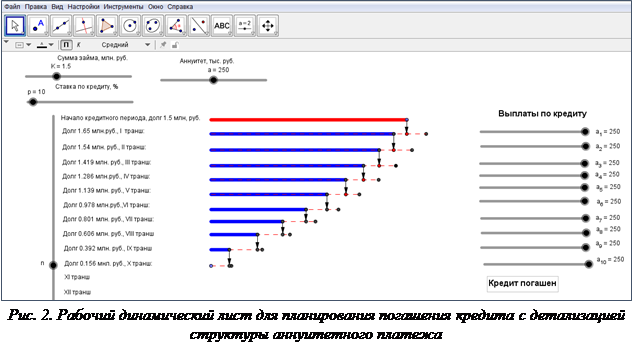
Для аналитического решения задачи у учащихся уже достаточно знаний, поэтому рабочий динамический лист здесь играет лишь роль средства вспомогательного характера, облегчающего учащимся получение обобщенного вывода об изменении соотношения долей при осуществлении четвертого транша. Для визуализации процесса изменения структуры аннуитетного платежа полезно выделить на модели отрезки, соответствующие различным его смысловым частям (рис. 2).
Учащиеся имеют возможность не только делать выводы на основе зрительного восприятия соотношения длин этих отрезков, но и измерять их инструментом «Расстояние или длина», а также использовать вычислительные возможности среды для прикидки значений долей.
Следующая задача вводит учащихся в ситуацию, которая вновь требует экспериментального исследования, так как установленный в договоре график платежей нарушается заемщиком.
Задача 5. Николай взял кредит 1,4 млн рублей 31 декабря 2013 года на условиях, представленных в задаче 1. Он хочет погасить его досрочно. Определите размеры выплат, если два года он будет придерживаться установленного графика, а 13 июня 2016 планирует покрыть остаток долга.
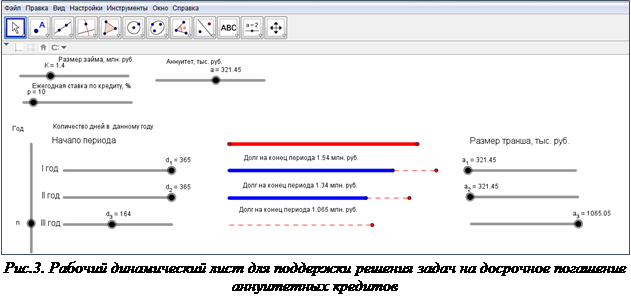
Для экспериментального решения задачи полезно использовать динамический лист, позволяющий самостоятельно устанавливать периодичность выплат и размеры траншей (рис. 3).
Динамический лист позволяет решить поставленную задачу в условиях отсутствия знаний о способах расчета процентных начислений на сумму долга за неполный период. Кроме того, работа с ним или анализ его устройства обеспечивают учащимся возможность вывода формулы расчета процентных начислений (r, у.е.) на сумму долга (S, у.е.) за неполный период (Т):
![]() (5)
(5)
Ее получение обеспечивает возможность аналитического решения данной задачи учащимся с целью уточнения суммы выплаты в последний год, которая была получена экспериментальным путем:
![]() (6)
(6)
Выводы
Представленный в статье учебный материал является лишь небольшим примером, на котором мы показали особенности привлечения систем динамической математики к изучению математических основ кредитования в школе. Предложенная серия задач может быть продолжена так, чтобы вывести учащихся на изучение нетиповых аннуитетных графиков (с отсрочкой на k лет/месяцев, с предварительной выплатой в течение k лет/месяцев процентов по кредиту и т.п.), а затем на изучение особенностей дифференцированных графиков погашения кредита, выбора наиболее выгодного из них [1]. Предложенные нами рабочие динамические листы позволяют имитировать действия кредиторов и заемщиков в учебном процессе, экспериментировать с динамическими моделями для исследования особенностей предлагаемых графиков погашения кредита, ставить новые задачи для формирования навыков поведения в кредитных ситуациях. Главным их достоинством является простота создания. К разработке таких динамических листов могут быть привлечены и сами учащиеся в рамках проектных работ.
Библиографическая ссылка
Николаев Р.Н., Шабанова М.В., Форкунова Л.В. ДИНАМИЧЕСКИЕ РАБОЧИЕ ЛИСТЫ В СИСТЕМЕ СРЕДСТВ ОБУЧЕНИЯ ВЫБОРУ ГРАФИКА ПОГАШЕНИЯ КРЕДИТА // Современные проблемы науки и образования. 2016. № 1. ;URL: https://science-education.ru/ru/article/view?id=24092 (дата обращения: 20.02.2026).
DOI: https://doi.org/10.17513/spno.24092



