Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ошоров Б.Б. 1

---

1 Восточно-Сибирский государственный университет технологий и управления

Исследуются неклассические краевые задачи Римана-Гильберта с разрывными граничными условиями для модельных систем уравнений первого порядка. В этот класс наряду с эллиптическими системами входят системы, не имеющие определенного типа по классификации Петровского. Вне зависимости от типа систем дается единообразная постановка задач и общая методика исследования их разрешимости в пространствах суммируемых функций с помощью априорных оценок. Эти задачи являются многомерными аналогами задачи Римана-Гильберта для системы уравнений Коши-Римана. Для модельной системы уравнений второго порядка в трехмерном пространстве, главная часть которой является второй степенью оператора Моисила-Теодореско, доказывается однозначная разрешимость трехмерного аналога ранее исследованной задачи Пуанкаре с разрывными краевыми условиями для системы Бицадзе. Коэффициенты предложенных систем являются симметрическими и кососимметрическими матрицами. По этой причине полученные результаты найдут применение при изучении общих систем уравнений.

Статья в формате PDF

194 KB

задача Пуанкаре

система Бицадзе

система Моисила-Теодореско

задача Римана-Гильберта

система Коши-Римана

априорная оценка

система уравнений с частными производными

1. Бицадзе А.В. Краевые задачи для эллиптических уравнений второго порядка. – М.: Наука, 1966. – 204 с.

2. 2, Векуа И.Н. Обобщенные аналитические функции. – 2 изд., перераб. – М.: Наука: гл. ред. физ.-мат. лит., 1988. – 512 с.

3. Ошоров Б.Б. Задачи Римана-Гильберта и Пуанкаре с разрывными краевыми условиями для некоторых модельных систем уравнений в частных производных //Дифференц. уравнения. – 2011. – Т.47, №5. – С. 696 – 704.

4. Ошоров Б.Б. Краевые задачи для одной модельной системы уравнений первого порядка в трехмерном пространстве//Дифференциальные уравнения. – 2015. – Т.51, №5. – С. 635 – 641.

5. Friedrichs K. O. Symmetric hyperbolic linear differential equations // Com. Pure Appl. Math. – 1954. V. 7, № 2. – P. 345–392.

     В данной работе речь пойдет о краевых задачах для систем уравнений с частными производными вида

                                         (1)

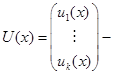где мультииндекс, , квадратные матрицы го порядка,  неизвестная матрица (вектор-функция),  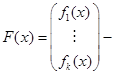заданная матрица (вектор-функция).

     Если в некоторой области выполнено условие

,                                  (2)

то система (1) называется эллиптической по Петровскому в этой области.

При  системы (1) имеют вид

                                 (3)

     Если все коэффициенты системы (3) симметрические матрицы, а одна из них положительно определена, то такие системы названы гиперболическими или системами Фридрихса [5].

     В классической постановке известные функции в задаче Римана-Гильберта для системы уравнений Коши-Римана и  в задаче Пуанкаре для эллиптической системы уравнений второго порядка непрерывны на границе области. Системы Фридрихса мы рассматривать не будем. Поэтому будем называть задачу неклассической, если рассматриваемая система уравнений не является эллиптической  или постановка задачи отличается от классических постановок.

     Для мерных вектор-функций  выражение  означает скалярное произведение в , а  и  – скалярное произведение и норму в пространстве . Нам также понадобятся пространства Соболева  со скалярным произведением  и нормой , причем

Неклассические задачи Римана-Гильберта

     Частным случаем системы уравнений (3) является эллиптическая система Коши-Римана

,

где

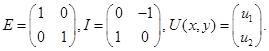
     Автором [3] для обобщенной системы Коши-Римана с младшими членами

доказана однозначная разрешимость неклассической задачи Римана-Гильберта [2] с разрывными краевыми условиями.

     Схема исследований следующая.     Пусть в пространстве  выделено подмножество  вектор-функций , принимающих на границе  заданные краевые условия,  оператор, формально сопряженный оператору , подмножество вектор-функций , удовлетворяющих сопряженным краевым условиям. Тогда имеет место

     Теорема 1. Если выполнены априорные оценки

то для  в пространстве  однозначно разрешима краевая задача

     Утверждение теоремы будет справедливым и для сопряженной задачи.

     В проведенных исследованиях нигде не используется эллиптичность системы. Поэтому возникло предположение, что тип системы в подобных задачах не оказывает существенного влияния на их корректность. Справедливость этой гипотезы нашла подтверждение в результатах, которые будут изложены ниже. При этом схема исследований остается той же, что позволяет ограничиться получением априорных оценок, на основании которых согласно теореме 1 делается вывод о корректности поставленной задачи.

     В прямоугольнике  рассмотрим систему уравнений

                                     (4)

 с коэффициентами

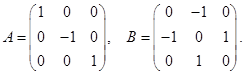                                    (5)   

При таких коэффициентах характеристическая форма (2) этой системы  будет формой третьего порядка, поэтому она не может быть знакоопределенной, т.е. система (4) неэллиптическая (неклассическая).

     Задача 1. В прямоугольнике  найти решение системы (4), (5), удовлетворяющее краевым условиям 

                         (6)

     Таким образом,  есть множество трехмерных вектор-функций , для которых выполнены краевые условия (6). Определим множество . Для этого рассмотрим интеграл , где , а  пока еще произвольная функция. Интегрируя по частям, получаем

если выполнены условия

                            (6*)

Множество   есть множество трехмерных вектор-функций , для которых выполнены условия (6*), формально сопряженный оператор имеет вид

.

     Лемма 1. Если матрица положительно определена в прямоугольнике , то имеют место априорные оценки

.

     Лемма 2. Если матрица  непрерывна в области  и существует число , такое что  и , то имеют место априорные оценки

     Сравнение условий (6) и (6*) с соответствующими условиями для системы Коши-Римана в работе [3] позволяет назвать задачу 1 неклассической задачей Римана-Гильберта с разрывными краевыми условиями.

     В работе [4] приведен пример задачи Римана-Гильберта с такими же условиями в трехмерном пространстве для неоднородной эллиптической системы уравнений Моисила-Теодореско

,                                                         (7)

где

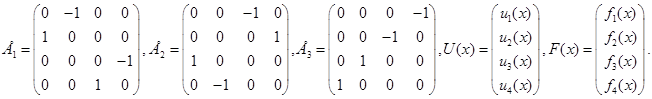Краевые условия

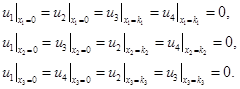                                               (8)

задаются на границе параллелепипеда , на каждой грани задается пара координатных функций, другая пара задается на противоположной грани, причем каждая из координатных функций задается только на трех гранях.

     Формально сопряженный оператор совпадает с самим оператором, в сопряженных краевых условиях каждая пара функций задается на противоположных гранях.

     Доказана однозначная разрешимость этой и сопряженной задачи в пространстве .

     Подобные постановки задач находят место и в пространствах большей размерности.

     Пусть  – параллелепипед в  В нем задана система уравнений

                                                 (9)   

где

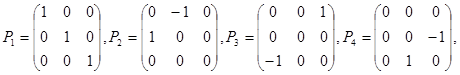
искомая и заданная трехмерная векторная функция соответственно.

     Характеристическая форма этой системы уравнений  имеет вид , поэтому система (9) не является эллиптической. Ее можно назвать системой составного типа.

     Задача 2. В параллелепипеде D найти решение системы уравнений (9) при условиях

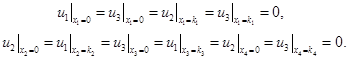                           (10)

     Лемма 3. Если матрица  достаточно “мала”, т.е. существует    такое, что  , то для любой вектор-функции   при условиях (10)справедливы оценки

          Доказательство лемм 1 – 3 проводиться методом интегрирования по частям.

Неклассические задачи Пуанкаре

     В работе автора [3] доказана однозначная разрешимость задачи Пуанкаре с разрывными краевыми условиями для эллиптической системы уравнений Бицадзе

,

где в главной части стоит вторая степень оператора Коши-Римана. Краевые условия Пуанкаре получаются из условий Римана-Гильберта добавлением новых условий. Следует отметить, что в случае, когда область, где рассматривается эта система, является  прямоугольником, краевые условия становятся условиями смешанной задачи для гиперболического уравнения второго порядка.

     Методы исследование этой задачи такие же, что и в предложенной выше схеме для систем первого порядка, и также как в случае задачи Римана-Гильберта нигде не используется эллиптичность системы.

     Подобные конструкции можно осуществить в трехмерном пространстве. Для оператора Моисила-Теодореско  непосредственно получаем , где оператор Лапласа. Следовательно, краевые условия (8) можно дополнить до условий Дирихле и для системы

                                                   (11)

будет корректной классическая задача Дирихле.

     Здесь предлагается неклассическая задача Пуанкаре с разрывными краевыми условиями.

Пусть

     Задача 3. В параллелепипеде  найти решение системы уравнений (11) при выполнении краевых условий (8) и дополнительных условий

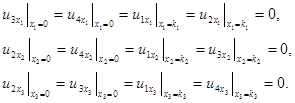                               (11)

     Лемма 4. Для любой вектор функции , удовлетворяющей условиям (8),(11) имеет место оценка  , где  

Следовательно, по обычной схеме исследуется разрешимость задачи 3 в пространстве с нормой .

     Можно поступить иначе. Из условий (8) и (11) следует, что вектор-функция  удовлетворяет сопряженным условиям (8). Уравнение  при этих условиях имеет единственное решение  . Тогда уравнение  при условиях (8) имеет единственное решение .

Заключение

Проведенные исследования показали, что тип системы уравнений в случае задач Римана-Гильберта и Пуанкаре с разрывными граничными условиями специального вида не является определяющим для корректности этих задач. Если посмотреть на структуру матричных коэффициентов в главной части приведенных выше систем уравнений, то можно заметить следующую картину. В системе Коши-Римана одна матрица симметрическая  положительно определенная (единичная), другая – кососимметрическая; в системе Моисила-Теодореско все матрицы кососимметрические; в системе уравнений (9) – одна матрица симметрическая и три другие кососимметрические; в системе Бицадзе – две матрицы симметрические и одна кососимметрическая; в последнем примере – все матрицы симметрические (единичные). Несмотря на это многообразие, краевые условия задаются по схожим принципам. Если учесть, что любая квадратная матрица представляется в виде суммы симметрической и кососимметрической матриц, то полученные результаты могут быть использованы при изучении систем уравнений с произвольными матричными коэффициентами.

Рецензенты:

Солдатов А.П., д.ф.-м.н., профессор, профессор кафедры математики Белгородского государственного национального исследовательского университета, г. Белгород;

Булдаев А.С., д.ф.-м.н., профессор, профессор кафедры прикладной математики Бурятского государственного университета, г.Улан-Удэ.

Библиографическая ссылка