Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Трубопроводы различного назначения имеют цилиндрическую структуру и могут обладать свойствами волноведущих структур для упругих волн, физические свойства которых рассматривались многими авторами [1,3–6]. В зависимости от поперечного распределения поля в волноведущих структурах возможно распространение различных типов волн (мод), число которых зависит от длины, размеров поперечного сечения и параметров сред, заполняющих волноведущие структуры [4]. Волновые процессы в трубопроводах имеют ту особенность, что  движение сред, заполняющих трубопроводы, приводит к невзаимности параметров прямых и обратных волн, наблюдающуюся в неограниченных средах [2–5]. Представляет интерес оценка степени невзаимности параметров волн различных мод в трубопроводе, заполненном движущейся средой.

Основные соотношения. Особенности невзаимных структур проявляются уже в конфигурации плоского волновода (), сформированного двумя жесткими границами, расположенными в плоскостях ,  (рис. 1). Волна распространяется вдоль оси . Волновод заполнен изотропной средой, характеризуемой плотностью  и скоростью распространения упругих волн в этой среде . Среда движется со скоростью вдоль оси волновода . Результирующая скорость волн в волноводе определяется решением волнового уравнения с учетом граничных условий при ,  и различается для волн в прямом и в обратном направлениях, что может быть использовано для измерения скорости движения среды в волноведущих структурах [2,3,6]. 

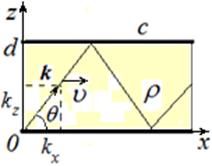
Рис.1. Плоский волновод, заполнен подвижной средой

            Комплексная амплитуда давления p(x,z) удовлетворяет уравнению Гельмгольца [4]:

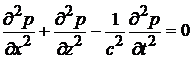                                                                                                         (1)

            Граничные для компонент скорости смещения частиц условия на жестких поверхностях волновода имеют вид:  [1]. Решение ищется в виде волны, распространяющейся вдоль оси волновода  и стоячей волны в поперечном направлении . С учетом граничных условий имеем:

                                   ,                                              (2)

            где задается граничными условиями,  – номер моды.  Подстановка искомого решения в волновое уравнение дает дисперсионное уравнение для волн, распространяющихся в волноводе, заполненном движущейся средой [1-4]:

                                                           ,                                                              (3)

, – угол, под которым направлен волновой вектор парциальной волны,  – компоненты волнового вектора , величина которого зависит от направления распространения волны:

 .

            Дисперсионное уравнение (3) может быть представлено в виде квадратного уравнения относительно :

,

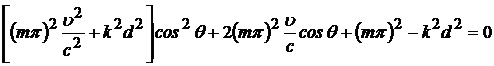            из которого следует, что распространение различных мод волн в волноводе с движущейся средой возможно при выполнении условия:

 ,

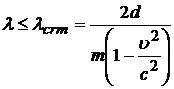где  – критическая длина прямых и обратных волн с индексом m, зависящая от относительной скорости среды (рис. 2). С ростом компоненты скорости движения среды вдоль оси волновода критические длины прямых и обратных волн всех мод возрастают.

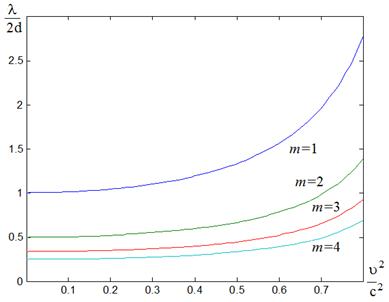
Рис. 2. Зависимость критических параметров мод от скорости движения среды

Основные результаты и выводы

            Анализ показывает, что различие параметров прямых и обратных волн растет с увеличением скорости движения среды в трубопроводе.

            Углы , под которым прямые и обратные парциальные волны распространяются по отношению к оси волновода, определяются из соотношения:

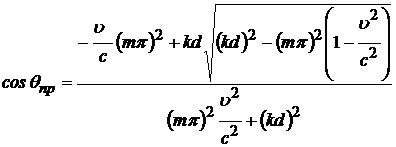
            Углы , под которым обратные парциальные волны распространяются по отношению к оси волновода, определяются из соотношения: 

.

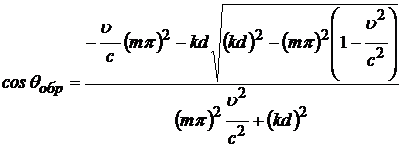В случае  (нулевая мода) имеем  для прямых и   для обратных волн.  

            При отсутствии движения среды  , для прямых и для обратных волн

                              

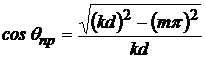
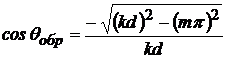
углы . Волновод имеет взаимные свойства.   В общем случае при  углы, под которыми распространяются прямые и обратные волны не совпадают .

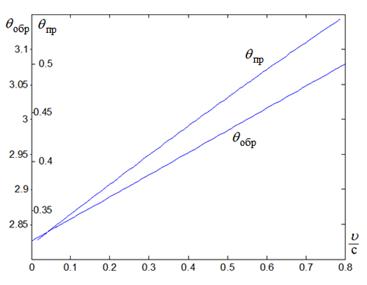
Рис.3. Зависимость углов падения в прямом и обратном направлениях от скорости

            С ростом индекса моды  и скорости движения среды  парциальные углы падения  между осью волновода и направлением распространения волны растут (рис.3).

            C увеличением скорости движения среды степень невзаимности структуры возрастает. В случае, когда скорость среды достигает скорости распространения волны в неподвижной среде (), структура приобретает свойство однонаправленности – одностороннее распространение волн (вентильный эффект). Скорость распространения волн в прямом направлении и равна 0 в обратном направлении. Зависимость постоянной распространения прямых и обратных волн зависит от скорости движения среды, равна

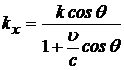
и сильно различается для прямых и обратных волн. Для различных мод  – показана на рис. 4.

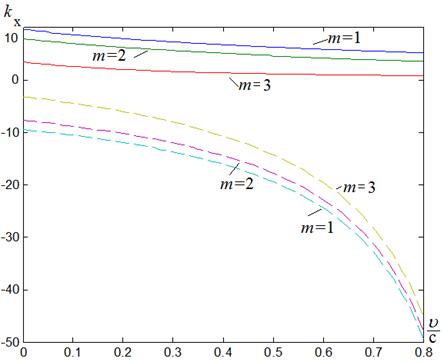
Рис. 4. Зависимость углов падения в прямом направлении для разных мод

от скорости движения среды

            Число мод, которые могут распространяться в волноводе, определяются соотношением:

,

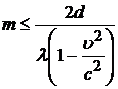где  – длина волны акустического сигнала. Таким образом, с ростом скорости движения среды , заполнением средой с малой скоростью распространения упругих волн , увеличением ширины волновода  и частоты  увеличивается число мод , для которых выполняется условие распространения.

            Выводы. Установлено, что движение среды, заполняющей акустический волновод, приводит к невзаимности его параметров в прямом и обратном направлениях. Степень невзаимности пропорциональна скорости движения среды. Скорость движения среды также влияет на скорость распространения акустических волн и приводит к изменению критических частот или критических длин волн мод волновода. С ростом скорости движения среды увеличивается число мод, для которых выполняется условие распространения.

Рецензенты:

Блатов И.А., д.ф.-м.н., профессор, заведующий кафедрой высшей математики, Поволжский государственный университет телекоммуникаций и информатики, г. Самара;

Тяжев А.И., д.т.н., профессор, профессор кафедры радиосвязи, радиовещания и телевидения, Поволжский государственный университет телекоммуникаций и информатики, г. Самара.