Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Время, в течение которого можно достоверно хранить, воспроизводить и передавать размер единиц величин, определяется в рамках модели «процесс – допустимая граница» [1, 2]. Данную модель можно охарактеризовать тремя основными параметрами: временем Т выхода метрологической характеристики x(t), характеризующей функционирование группового эталона, за пределы допуска; вероятностью U работоспособного состояния группового эталона в заданный момент времени; границами Gd допусков на параметры.

Цель работы: постановка задачи определения метрологических характеристик автономных средств измерений на основе решения уравнения Фоккера-Планка-Колмогорова.

Рассмотрим модель на основе уравнения Фоккера-Планка-Колмогорова. При использовании данной модели считается, что работоспособность групповых эталонов (возможность достоверно хранить, воспроизводить и передавать размер единицы величины) обеспечивается поддержанием их характеристик в границах допустимой области. Метрологический отказ – это выход хотя бы одного параметра за эти границы.

Состояние х0 = x(tGd), при котором x(t) находится в области Gd, соответствует работоспособному состоянию группового эталона, а состояние хт = х(т) – отказу, при этом условие работоспособности будет

,                                  (1)

где x(t) – вектор метрологических характеристик группового эталона;

P{·} – вероятность соответствующего события.

Для использования рассмотренной модели надежности типа «процесс – допустимая граница» задаются законом эволюции метрологических характеристик в виде диффузионного марковского процесса.

В условиях эксплуатации групповых эталонов единиц величин при нахождении межповерочных интервалов возникает необходимость учета метрологических характеристик, определяющих состояние метрологической исправности групповых эталонов. В качестве таких характеристик, как правило, используются основная погрешность, среднеквадратическое отклонение (СКО) случайной составляющей погрешности и некоторые другие. Если состояние метрологической исправности определяют несколько метрологических характеристик, то из них выбирается та, по которой обеспечивается наибольший процент брака при поверках. В дальнейшем, в качестве такой характеристики воспользуемся основной погрешностью групповых эталонов. С учетом нелинейности преобразований метрологических характеристик, характеризующих функционирование групповых эталонов, определение времени выхода метрологических характеристик, за пределы допуска должно осуществляться на основе решения эволюционных уравнений (типа Фоккера-Планка-Колмогорова). При этом для обеспечения гарантированного определения необходимо обеспечить высокую точность решения эволюционных уравнений.

Так как точное решение эволюционных уравнений возможно лишь в редких случаях [5], то на практике, как правило, ограничиваются применением различных приближенных численных методов интегрирования [3]. При этом большинство из этих методов связано с необходимостью проведения численного интегрирования системы обыкновенных дифференциальных уравнений, описывающей эволюцию во времени параметров, характеризующих априорную плотность вероятности для уравнения Фоккера-Планка-Колмогорова.

Применение аппарата теории марковских процессов для анализа моделей эволюции метрологических характеристик группового эталона, описанных дифференциальными уравнениями (с указанием начальных и граничных условий) или функциональных соотношений, предполагает разработку общего подхода к анализу метрологических характеристик, описываемых эволюционными уравнениями. При этом должны соблюдаться изложенные ранее требования к моделям эволюции метрологических характеристик и последовательно выполняться следующие этапы:

-проверка соответствия рассматриваемого процесса эволюции метрологических характеристик группового эталона марковскому;

-если рассматриваемый процесс марковский, то вычисление локальных характеристик процесса: коэффициентов сноса и диффузии;

-запись уравнения Фоккера-Планка-Колмогорова и указание соответствующих начальных и граничных условий для плотности вероятности p(t, λ);

-нахождение точного или приближённого решения уравнения Фоккера-Планка-Колмогорова тем или иным методом.

Одним из основных преимуществ аппарата марковских процессов является возможность определения метрологических характеристик группового эталона единицы величины на основе решения задачи определения времени первого достижения границы [2, 4].

Математическая постановка задачи.    Пусть Δ1, Δ2,…, Δr – множество r независимых основных погрешностей хранителей группового эталона, распределённых по нормальному закону

                            (2)

Согласно центральной предельной теореме совместное распределение основных погрешностей хранителей группового эталона Δi,  характеризующее основную погрешность группового эталона λ также нормально [3].

В качестве основной погрешности группового эталона принимается некоторая функция от погрешностей хранителей l. Процесс изменения которой может быть представлен в виде приближённого к винеровскому процесса, являющегося гауссовским нестационарным процессом с нулевым математическим ожиданием и дисперсией, пропорциональной времени, определяемым c помощью стохастического дифференциального уравнения

.                                   (3)

            На рис. 1 представлена графическая модель эволюции основной погрешности группового эталона.

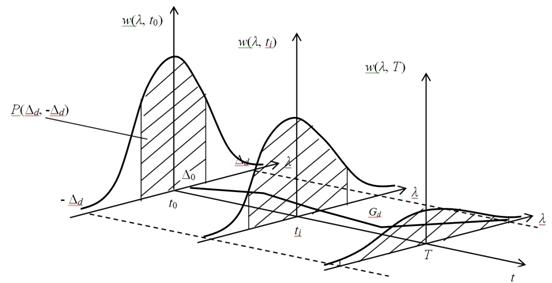
Рис.1. Эволюция основной погрешности группового эталона

 

В качестве метрологического отказа группового эталона принимается выход его основной погрешности λ за границу допустимых значений –Δd и Δd области Gd. Тем самым, вероятностью безотказной работы группового эталона будет вероятность U(λ, t) не выхода процесса эволюции основной погрешности группового эталона λ(t) из этой области

,         (4)

где U(λ, t) – вероятность того, что ордината λ процесса λ(t) ни разу не выйдет за границы допустимой области  на интервале [t0, T] при условии, что в начальный момент времени t=t0 значение основной погрешности группового эталона λ=λ0 находилась в допустимой области Gd.

            С учетом марковских свойств приближённого к винеровскому процесса  эволюция плотности распределения основной погрешности хранителя единицы величины удовлетворяет следующим дифференциальным уравнениям в частных производных (уравнению Фоккера-Планка-Кологорова) в обратном времени [4]

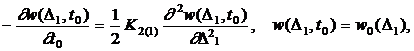               (5)

где  - плотности распределения основной погрешности хранителя группового эталона;

- коэффициент диффузии изменения основной погрешности хранителя группового эталона Δ1(t).

            Сделав замену переменных t = T – t0, получаем

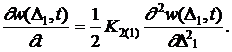                                   (6)

            Второе (прямое) уравнение Фоккера-Планка-Колмогорова запишется в виде

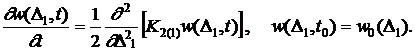             (7)

            Таким образом, при задании граничных условий, исходя из конкретной задачи, характеристики группового эталона в момент достижения границ допустимой области могут быть получены с учётом соотношений (5) – (7). Границы задаются требованиями ГОСТов, технических условий, других руководящих документов.

Для многомерного случая математическая постановка задачи определения метрологических характеристик группового эталона с использованием эволюционных уравнений выглядит следующим образом. С учетом марковских свойств приближённого к винеровскому процесса (4) плотность распределения основной погрешности группового эталона удовлетворяет следующему прямому уравнению Фоккера-Планка-Кологорова [4, 6, 7]

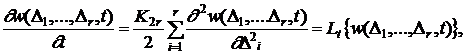
, ,                  (8)

где - совместная плотность распределения основных погрешностей хранителей группового эталона Δi,

K2r – коэффициент диффузии изменения основной погрешности группового эталона.

Lt – оператор ФПК эволюционного уравнения.

Для построения эволюционного уравнения требуется определить ло­кальные характеристики исследуемого процесса. В случае винеровского описания (8) необходимо определить коэффициент диффузии изменения основной погрешности группового эталона K2r. Данная задача может быть решена на основе исследования случайной и неисключённой систематической погрешности группового эталона [6,7].

В качестве основных показателей определения метрологических характеристик группового эталона выбрана точность при условии обеспечения заданной (гарантированной) достоверности воспроизведения единицы величины.

Для определения метрологических характеристик по результатам взаимных сличений хранителей группового эталона в условиях метрологической автономности прията модель основной погрешности хранителя единицы величины вида

 ,                                    (9)

где  -  значение единицы величины i – го хранителя группового эталона;

Х0 – значение единицы величины исходного эталона.

Система уравнений взаимных сличений хранителей группового эталона представлена выражением

,  (10)

где  - взаимная основная погрешность j-го хранителя;

ni(j)  –  шумы сличений.

Поскольку групповой эталон может быть сформирован как из равноточных так и неравноточных хранителей, необходимо ввести в систему (8) некоторые весовые коэффициенты сличений, являющиеся функцией от допустимых погрешностей соответствующих хранителей

.                                (11)

Система весовых уравнений взаимных сличений хранителей группового эталона примет вид

 .            (12)

Таким образом, теоретической основой построения автономных средств измерений может является разработка высокоточных методов определения основных метрологических характеристик группового эталона посредством решения уравнения Фоккера-Планка-Колмогорова (8) для приближенной к винеровской модели эволюции основной погрешности  с совместным решением системы весовых уравнений взаимных сличений хранителей группового эталона.

Выводы

Метрологические характеристики автономных средств измерений изменяются в процессе эксплуатации. Законы эволюции метрологических характеристик, характеризуются различными математическими зависимостями, как правило, - нелинейными и являются стохастическими. Для оценки состояния любого средства измерений в будущие моменты времени необходимо выбрать адекватную модель эволюции его метрологических характеристик [8, 9]. Дрейф метрологических характеристик автономных средств измерений представляется в виде нелинейного инерционного преобразования, описанного соответствующими дифференциальными уравнениями. Наиболее точное решение подобных уравнений получается при условии марковской аппроксимации процесса эволюции метрологических характеристик. Точное решение эволюционных уравнений возможно лишь в редких случаях, поэтому на практике, как правило, ограничиваются применением различных приближенных численных методов интегрирования. При этом большинство из этих методов связано с необходимостью проведе­ния численного интегрирования системы обыкновенных дифференциальных уравнений, описывающей эволюцию во времени параметров, характеризующих априорную плотность вероятности для уравнения Фоккера-Планка-Колмогорова.  В качестве основной метрологической характеристики (погрешности) группового эталона принимается некоторая функция от погрешностей хранителей, процесс изменения которой представляется в виде приближённого к винеровскому процесса.

Рецензенты:

Звездина М.Ю., д.ф.-м.н., доцент, зав. кафедрой «Радиоэлектроника», Федеральное государственное бюджетное образовательное учреждение высшего профессионального  образования  «Донской государственный технический университет», г. Ростов-на-Дону.

Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, Федеральный научно-производственный центр ФГУП «РНИИРС», г. Ростов-на-Дону.