Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Блинов А.В. 1 Максимов П.В. 1 Шиверский А.В. 1 Горохов А.Ю. 1

---

1 ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет»

С помощью разработанной динамической параметрической конечно-элементной модели, описывающей волновые процессы, происходящие в трубопроводе под действием внешних возмущений, проводится серия вычислительных многофакторных экспериментов с целью установления влияния локальных изменений, дефектов, повреждений в трубопроводе на спектр вынужденных колебаний в некоторой исследуемой точке, соответствующей месту возможной установки измерительной аппаратуры. Исследуется влияние дефекта на фронт распространения волны и амплитудно-частотную характеристику полученных сигналов в зависимости от размеров трещины. Показано, что анализ АЧХ поля перемещений на поверхности трубопровода позволяет определить наличие трещины и ее размер. В процессе анализа набора полученных численных решений для различных размеров трещин получено, что в результате возможно создание прикладной методики анализа пригодности исследуемого трубопровода к дальнейшей эксплуатации и оценки его текущего состояния (определение наличия трещин), проводимых на основании серии динамических испытаний.

Статья в формате PDF

403 KB

метод конечных элементов

динамика

моделирование

вибродиагностика

1. Блинов А.В., Максимов П.В. Постановка динамической задачи распространения упругих волн в трубопроводе // Международный научно-исследовательский журнал. – 2014. - №11(30) часть 2. – С 48-50.

2. Блинов А.В. Максимов П.В. Разработка и верификация нестационарной конечно-элементной модели для исследования волновых процессов в трубопроводе // Современные проблемы науки и образования. – 2015. - №1

3. Бочкарев Н.Н., Курочкин А.А. Вибродиагностический контроль движения внутритрубных объектов в магистральных газопроводах // Электронный научный журнал «Нефтяное дело». – 2012. –№5. –С.86-98.

4. Денисов Г.Г. Об импульсе волн при продолжительных колебаниях упругого стержня / Г.Г. Денисов, В.В. Новиков, М.Л. Смирнов // Вестник Нижегородского университета им. Н.И. Лобачевского. – 2010. - №5-1. С. 134-137.

5. Зенкевич О.С. Метод конечных элементов в технике. / Б.Е. Победря – М.: Мир, 1975. – 543 с.

6. Сальников А.Ф., Сальников С.А., Щелудяков А.М. Оценка влияния динамических нагрузок на остаточную работоспособность полимерноармированных труб // Газовая промышленность. –2014. –№1(701). –с.52-55.

7. Цветков Р.В., Шардаков И.Н., Шестаков А.П. Анализ распространения волн в подземных газопроводах применительно к задаче проектирования систем мониторинга // Вычислительная механика сплошных сред. – 2013. –Т.6, №3. –С.364-372.

8. Щелудяков А.М., Сальников А.Ф., Дутлов О.А. Волновая диагностика трубопроводов из полимерно-армированных труб // Модернизация и научные исследования в транспортном комплексе. -Т.1. -2014. -с.254-258.

Трубопровод – инженерное сооружение, предназначенное для транспортировки газообразных и жидких веществ. Актуальными являются задачи, связанные с эксплуатацией трубопровода и его ремонтом [3, 7]. Авторами предпринята попытка математического обоснования основанной на принципах вибродиагностики методики оценки остаточной работоспособности трубопроводов. В рамках текущей работы, на основании серии вычислительных экспериментов оценивается возможность определения типа, размера и местоположения дефекта трубопровода путем анализа закономерностей распространения упругих волн в материале трубопровода и оценки спектральных характеристик поля перемещений в локальной области на поверхности трубы. Разработанные в результате исследований математические и компьютерные модели динамических систем представлены в виде виртуальных прототипов, на основе которых разрабатываются расчетные методики проектирования металлургической продукции с применением современных CAD/CAE-систем; научно обосновываются методы вибродиагностики и дефектации готовой продукции высокотехнологичных предприятий.

Объект исследования

Объектом исследования является участок трубопровода, нагруженного внутренним давлением. На внешней и внутренней поверхности трубопровода в результате нарушений технологии производства, либо в процессе эксплуатации возможно образование трещин, снижающих эксплуатационные характеристики трубопровода, приводящих в разрушению конструкции. Оценку размеров трещин и их расположения предлагается проводить на основании анализа картины распространения в трубопроводе упругих волн [4]. Рассматривается участок трубопровода, на одном конце которого расположено регистрирующее устройство, определяющее перемещения точек поверхности исследуемого объекта. Упругие колебания среды вызываются импульсной нагрузкой, приложенной к другому концу трубопровода. Исследуется поле перемещений вблизи регистрирующего устройства, определяется спектр частот вынужденных колебаний поверхности.

Математические и компьютерные модели исследуемого объекта

Для отработки методических подходов к созданию расчетной методики анализа работоспособности трубопроводов на более простых моделях, на текущем этапе задача решалась в осесимметричной постановке для трубы, выполненной из изотропного материала [1, 5]. В рамках общего исследования проблемы выполнено [2]:

1. Построена математическая осесимметричная модель трубопровода, содержащего трещины, неоднородности материала и иные дефекты. Трещины на внутренней и внешней поверхностях трубопровода учитываются в виде дополнительных свободных поверхностей, неоднородности материала – путем локального изменения свойств материала

2. Разработаны нестационарные диссипативные конечно-элементные модели распространения упругих волн в материале трубопровода. Ряд параметров численных моделей задается на основании проведенных ранее натурных экспериментов [6, 8.].

3. Выполнена верификация разработанных численных моделей.

4. Проведена серия вычислительных экспериментов для изучения картины распространения упругих волн, вызванных приложением импульсного силового воздействия с известными характеристиками.

5. Определен динамический отклик системы в характерных точках.

В данной работе, для серии полученных ранее численных решений задачи о распространения упругих волн в трубопроводе, содержащим дефекты, трещины или локальные неоднородности, анализируются амплитудно-частотные характеристики поля перемещений в предполагаемой точке практического измерения вынужденных колебаний поверхности трубопровода вибро-акустической аппаратурой. Для проведения спектрального анализа нестационарного поля перемещений точек на поверхности трубопровода использован алгоритм Быстрого преобразования Фурье.

Анализ волнового процесса в трубопроводе с дефектом (трещиной)

Для предварительно определенных полей перемещений конструкции [2], содержащей повреждения в виде трещины, начинающейся на внешней поверхности трубопровода и распространяющейся вдоль радиуса вглубь материала на величину h проведен спектральный анализ системы и выполнено исследование влияния возможного дефекта на амплитудно-частотные характеристика (АЧХ) конструкции. Некоторые наглядные изображения спектров для трещин с длинами h=0.3*H и h=0.5*H (где H – толщина трубопровода), а также для конструкции без повреждений показаны на рисунках 1-3.

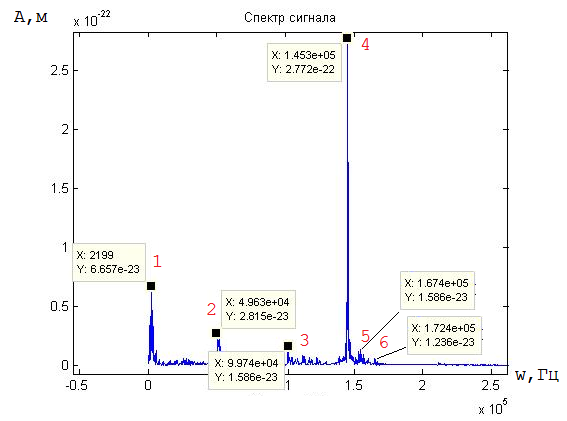
Рис. 1. Спектр сигнала для трубопровода без повреждений

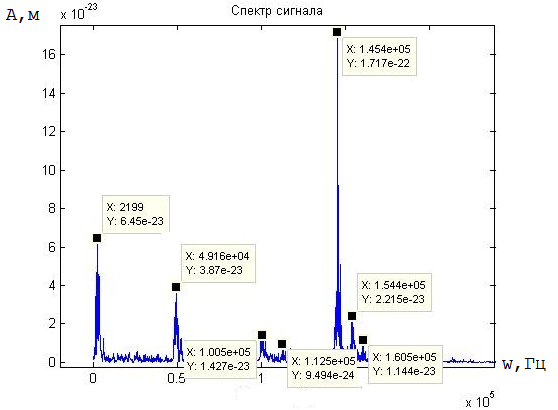
Рис. 2. Спектр сигнала для трубопровода с трещиной, глубиной h=0.3 H

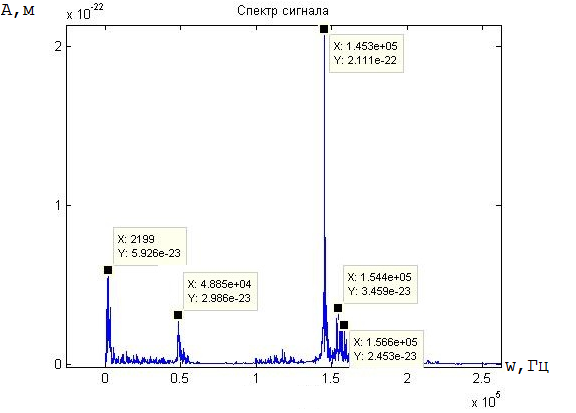
Рис. 3. Спектр сигнала для трубопровода с трещиной, глубиной h=0.5 H

На рисунке 1 красными цифрами отмечены ключевые гармоники, значения частот отмеченных гармоник и амплитуды колебаний приведены в таблицах 1 и 2 соответственно.

Таблица 1

Зависимость частот от длины трещины

Таблица 2

Зависимость амплитуд гармоник от длины трещины

Из таблицы 1 видно, что наличие в трубопроводе трещины приводит к изменению спектральных характеристик конструкции, при этом, ряд характерных гармоник остаются неизменными (гармоники 1, 4), а некоторые гармоники сдвигаются, причем степень их изменения зависит от величины повреждения трубопровода (гармоники 2, 3, 6).

Анализ зависимости амплитуд гармоник от величины повреждения в текущей постановке задачи проводить нецелесообразно, так как величины амплитуд колебаний зависят от диссипативных свойств материала трубопровода; для корректного описания особенностей процесса затухания распространения упругих волн в среде, определения коэффициентов диссипации требуются дополнительные натурные эксперименты.

Заключение

С помощью разработанной динамической параметрической конечно-элементной модели, описывающей волновые процессы, происходящие в трубопроводе под действием внешних возмущений, проведена серия вычислительных многофакторных экспериментов с целью установления влияния локальных изменений, дефектов, повреждений в трубопроводе на спектр вынужденных колебаний в некоторой исследуемой точке, соответствующей месту возможной установки измерительной аппаратуры. Исследовано влияние дефекта на фронт распространения волны и амплитудно-частотную характеристику полученных сигналов в зависимости от размеров трещины. Показано, что анализ АЧХ поля перемещений на поверхности трубопровода позволяет определить наличие трещины и ее размер.

Анализ набора полученных численных решений для различных размеров трещин показал, что в результате возможно создание прикладной методики анализа пригодности исследуемого трубопровода к дальнейшей эксплуатации и оценки его текущего состояния (определение наличия трещин), проводимых на основании серии динамических испытаний.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.31.0068 от 23.05.2013 г. в составе мероприятия по реализации постановления Правительства РФ № 218).

Рецензенты:

Шевелев Н.А., д.т.н., профессор кафедры «Динамика и прочность машин» ФГБОУ ВПО Пермский национальный исследовательский политехнический университет , г. Пермь;

Сметанников О.Ю., д.т.н., профессор кафедры «Вычислительная математика и механика» ФГБОУ ВПО Пермский национальный исследовательский политехнический университет ,г. Пермь.

Библиографическая ссылка