Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Румянцев Д.Е. 1, 3 Епишков А.А. 1 Липаткин В.А. 1 Волкова Г.Л. 2

---

1 ФГБОУ ВПО «Московский Государственный Университет Леса»

2 ФГБУ «Институт глобального климата и экологии Росгидромета и РАН»

3 ФГБУ «Институт географии РАН»

Ряды радиального прироста древесных растений характеризуются вариабельностью внутри одной ценопопуляции. Размах вариации этих рядов по разным показателям в настоящее время слабо изучен. Одним из теоретически и практически важных показателей является уровень синхронности между дендрохронологическими рядами. Исследования включали хронологии сосны обыкновенной (Pinus sylvestris L.) из Бабаевского лесничества Вологодской области; Муромцевского лесничество Владимирской области; Краснобаковского лесничества Нижегородской области. Для каждой из областей было получено по два массива значений коэффициента синхронности (при правильной и экспериментально заданной неправильной датировке). Все три массива значений коэффициента синхронности при экспериментально заданной неправильной датировке согласно оценке по критерию Колмогорова—Смирнова при уровне значимости 0,01 имеют одинаковый закон распределения. Массивы значений при правильной датировке имеют разные законы распределения, что, видимо, обусловлено разной ценопопуляционной структурой анализируемых популяций.

Статья в формате PDF

226 KB

дендрохронология

временные ряды радиального прироста

коэффициент синхронности

перекрестная датировка

1. Битвинскас Т.Т. О некоторых вопросах синхронизации (верификации) в дендроклиматохронологических исследованиях и о принципах классификации и отбора дендрохронологического материала // Материалы Второго Всесоюзного совещания по дендрохронологии и дендроклиматологии «Дендроклиматохронология и радиоулерод». – Каунас: Ин-т ботаники АН Литовской ССР, 1972 – С. 148–158.

2. Воронин В.И., Осколков В.А. Как бороться с катастрофой сибирских лесов – незаконными рубками? // Материалы конференции «ДЕНДРО 2012: перспективы применения древесно-кольцевой информации для целей охраны, воспроизводства и рационального использования древесной растительности». М.: МГУЛ, 2013 – С. 24–25.

3. Вахнина И.Л. Применение дендрохронологического метода исследований при проведении экспертизы по незаконным рубкам // Успехи современного естествознания, 2014. — № 5-2. — С. 73–75.

4. Жаворонков Ю.М. Судебная дендрохронология на службе криминалистики XXI века // Вестник Московского государственного университета леса – Лесной Вестник. – 2014. — № 5 (18) – С. 53–58

5. Липаткин В.А., Пальчиков С.Б., Румянцев Д.Е., Жаворонков Ю.М. Возможности использования метода перекрестной датировки древесно-кольцевых хронологий при расследовании дел, связанных с незаконной заготовкой древесины // Теория и практика судебной экспертизы. Научно-практический журнал. – 2010. — № 3(19) – С. 244–254.

6. Липаткин В.А., Пальчиков С.Б., Румянцев Д.Е., Крылов А.М., Епишков А.А. Возможности исследования дендрохронологической информации при исследованиях лесозащитных страт Муромцевского лесничества // Вестник Московского государственного университета леса – Лесной вестник. – 2013. — № 7(99) — С. 115–120

7. Ловелиус Н.В., Дьяконов К.Н., Пальчиков С.Б., Ретеюм А.Д., Румянцев Д.Е., Липаткин В.А., Черакшев А.В. Радиальный прирост сосны в сфагновых сосняках лесной зоны России и глобальные факторы среды // Общество. Среда. Развитие. – 2013. — № 4 (29) – С. 251–259

8. Майорова Е.И., Гончарук Н.Ю. К вопросу использования дендрохронологического анализа в судебно-экспертной практике // Вестник Московского государственного университета леса – Лесной вестник. – 2015. — № 5. – С. 153–157.

9. Синкевич С.М. Дендрохронология в судебной экспертизе: ограничения и перспективы // Вестник Московского государственного университета леса – Лесной Вестник. – 2014. — № 5 (18) – С. 166–171

10. Wolodarsky-Franke A., Lara A. The role of «forensic» tree-ring analysis in the conservation of alerce (Fitzroya cupressoides ((Molina) Johnston)) forests in Chile //Dendrochronology. – 2005. — Vol. 22. – № 3. – P. 235–240.

Ряды радиального прироста древесных растений характеризуются вариабельностью внутри одной ценопопуляции. Размах вариации этих рядов по разным показателям в настоящее время слабо изучен. Одним из теоретически и практически важных показателей является уровень синхронности между дендрохронологическими рядами. В первом приближении можно утверждать, что, чем выше уровень генетического подобия между особями, тем выше уровень взаимной синхронности между хронологиями. С практической точки зрения важно выяснить, в каких пределах может варьировать коэффициент синхронности при случайно обусловленном сходстве хронологий. Для исследования этого вопроса Т.Т. Битвинскас [1] предложил ставить эксперименты с созданием заведомо неверной взаимной датировки двух хронологий друг относительно друга. Таким образом, может быть установлен размах варьирования синхронности хронологий при случайном уровне сходства. Знание этих закономерностей может послужить целям решения экспертных задач. В то же время существуют ситуации, когда перекрестная датировка на основе коэффициентов синхронности невозможна из-за большого числа выпавших годичных колец. Однако даже в таких ситуациях полезно знать о факте неправильной взаимной датировки двух хронологий друг относительно друга и уровне вероятности данного вывода. Использование метода перекрестной датировки важно для решения ряда вопросов, возникающих при проведении экспертиз по незаконным рубкам леса [2, 3, 4, 5, 9, 10]. В то же время отмечается, что совершенствование экспертной техники исследований при перекрестной датировке должно вестись с учетом анализа природной изменчивости коэффициентов сходства между дендрохронологическими рядами [8].

Материалы и методы

Исследования включали хронологии сосны обыкновенной (Pinus sylvestris L.) из Бабаевского лесничества Вологодской области; Муромцевского лесничества Владимирской области; Краснобаковского лесничества Нижегородской области. Для каждой из областей было получено по два массива значений коэффициента синхронности (при правильной и экспериментально заданной неправильной датировке). Обработка полученных данных выполнялась с помощью программы TSAP-Win. Для каждой пробной площади, характеризующей отдельную ценопопуляцию сосны, был произведен расчет коэффициентов синхронности между средней групповой хронологией и индивидуальными хронологиями. Эти данные составили массив значений коэффициента синхронности для случаев правильной датировки. Он включал в себя 1861 вариант.

На втором этапе производилось моделирование искусственно заданной неправильно датировки индивидуальной хронологии относительно средней групповой хронологии. В программе TSAP-Win каждая индивидуальная древесно-кольцевая хронология сдвигалась на один год назад по сравнению с групповой средней (эталонной) хронологией, и производился расчет коэффициента синхронности. Максимальный период сдвига составлял 5 лет. Таким способом был получен массив значений коэффициента синхронности при заведомо неправильной перекрестной датировке. Он включал в себя 9352 варианта.

Числовые характеристики всех полученных распределений коэффициентов синхронности представлены в таблице 1.

Таблица 1

Объем выполненных полевых работ

Подробно методика работ была описана в предыдущих публикациях [6, 7]. Пробные площади закладывались в таксационных выделах средневозрастных, приспевающих и спелых древостоев I–III бонитета. Отбор образцов древесины производился с помощью бурава Пресслера с деревьев I–III класса роста по Крафту, отбор велся на высоте 1,3 м по произвольно взятому радиусу.

Обработка полученных данных выполнялась с помощью программы TSAP-Win. Для каждой пробной площади, характеризующей отдельную ценопопуляцию сосны, был произведен расчет коэффициентов синхронности между средней групповой хронологией и индивидуальными хронологиями. Эти данные составили массив значений коэффициента синхронности для случаев правильной датировки. Он включал в себя 1861 вариант. На втором этапе производилось моделирование искусственно заданной неправильно датировки индивидуальной хронологии относительно средней групповой хронологии. В программе TSAP-Win каждая индивидуальная древесно-кольцевая хронология сдвигалась на один год назад по сравнению с групповой средней (эталонной) хронологией, и производился расчет коэффициента синхронности. Максимальный период сдвига составлял 5 лет. Таким способом был получен массив значений коэффициента синхронности при заведомо неправильной перекрестной датировке. Он включал в себя 9352 варианта.

Результаты и обсуждение

Для полученных массивов значений коэффициента синхронности при правильной и при неправильной датировке были рассчитаны значения частоты встречаемости в выборке. Они отражены на графиках на рисунке 1.

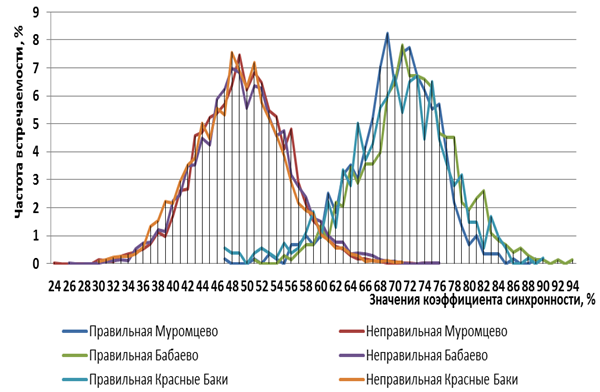
Рис. 1. Графики относительных частот встречаемости коэффицентов синхронности при правильной и искусствено смоделированной неправильной датировке древесно-кольцевых хронологий в популяциях сосны обыкновенной из Владимирской, Нижегородской и Вологодской областей

Была проведена статистическая обработка данных, результаты которой отражены в таблице 1. Из приведенной таблицы 1 видно, что средние значения коэффициентов синхронности для всех трех рассматриваемых участков при правильной датировке значительно выше, чем при неправильной датировке. Значимость различий между распределениями частот встречаемости значений коэффициента синхронности при правильной и неправильной датировке подтверждается для всех трех участков по критерию Колмогорова—Смирнова (уровень значимости 0,05). При этом средние значения при правильной датировке во всех трех областях близки между собой. Для искусственно смоделированной неправильной датировки аналогично – средние значения коэффициента синхронности практически совпадают для трех различных областей.

Таблица 2

Статистическая характеристика массивов распределений значений коэффициентов синхронности

Для проверки однородности массивов значений коэффициента синхронности при правильной и неправильной датировке на трех рассматриваемых площадях объединим все полученные значения коэффициентов синхронности в один массив и проведем разбиение на два кластера с помощью метода кластеризации К-средних. Данный алгоритм позволяет таким способом разделить исходные наблюдения на заданное число кластеров, чтобы дисперсия между кластерами была максимальна, а внутри кластеров – минимальна. Иными словами, данный метод позволяет разбить наблюдения на заданное число групп так, чтобы внутри каждой из групп значения были максимально однородны и при этом эти сами группы значительно отличались между собой. Ниже приведены результаты разбиения всего массива коэффициентов на две группы (табл. 3).

Таблица 3

Результаты кластеризации массива значений коэффициента синхронности

При этом из коэффициентов, полученных при правильной датировке во всех рассматриваемых областях, 97% вошли в первый кластер, а из коэффициентов, полученных при неправильной датировке, во второй кластер вошли 93%. При этом центр первого кластера близок к средним значениям коэффициентов синхронности при правильной датировке для всех трех рассматриваемых участков, а центр второго кластера – к средним значениям при неправильной датировке. Таким образом, массивы значений коэффициента синхронности для всех трех областей при правильной и неправильной датировке составляют две однородные группы, при этом различия в средних значениях между правильной и неправильной датировкой статистически значимы.

Гипотеза о нормальном распределении массивов значений коэффициента синхронности (при правильной и неправильной датировке) в ходе выполненных статистических расчетов была отвергнута из-за значимо отличных от нуля коэффициентов асимметрии и эксцесса. В дальнейшем для сравнения распределений по пробным площадям использовались непараметрические критерии (для их применения не требуется нормальность исходных данных).

Далее мы провели попарное сравнение всех массивов правильных коэффициентов между собой по критерию Колмогорова—Смирнова. Аналогичную процедуру проделали с тремя массивами коэффициентов при неправильной датировке. Критерий Колмгорова—Смирнова позволяет сравнить частоты в двух эмпирических функциях распределения и проверяет гипотезу об однородности выборок (гипотезу о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности). При этом нулевой гипотезой является то, что различия между распределениями недостоверны, а альтернативной гипотезой является достоверность различий.

Результаты сравнения представлены в виде таблицы 4.

Таблица 4

Сравнение массивов значений коэффициента при правильной и экспериментально заданной неправильной датировке

В таблице 4 для каждой пары сравнений приведено p-значение (p-value) – вероятность ошибки при отклонении нулевой гипотезы. Если p-значение меньше заданного уровня значимости, то нулевая гипотеза отвергается в пользу альтернативной, если p-значение больше заданного уровня значимости альфа, то нулевая гипотеза на данном уровне значимости принимается. Таким образом, если p-значение > 0,05, различия между выборками признаются недостоверными на уровне значимости 0,05. Аналогично, если p-значение > 0,01, гипотеза об одинаковом распределении двух выборок не отвергается на уровне значимости 0,01.

Сравнение двух массивов значений коэффициента синхронности при правильной датировке из Нижегородской и Владимирской области показало, что по критерию Колмогорова—Смирнова данные массивы принадлежат к одному закону распределения (различия в частотах между выборками недостоверны) на уровне значимости α = 0,18, а, следовательно, также на стандартных уровнях значимости 0,05 или 0,01.

Сравнение двух массивов значений коэффициента синхронности при правильной датировке из Нижегородской и Вологодской области показало, что по критерию Колмогорова—Смирнова данные массивы принадлежат к одному закону распределения (различия в частотах между выборками недостоверны) на уровне значимости α = 0,0016. Данный уровень значимости ниже, чем стандартные 0,05 и 0,01, и это означает опровержение гипотезы об одинаковых распределениях – между выборками есть статистически значимые различия.

Сравнение двух массивов значений коэффициента синхронности при правильной датировке из Вологодской и Владимирской области показало, что по критерию Колмогорова—Смирнова данные массивы принадлежат к одному закону распределения (различия в частотах между выборками недостоверны) на уровне значимости α = 0,0001. Данный уровень значимости ниже, чем стандартные 0,05 и 0,01, и это означает опровержение гипотезы об одинаковых распределениях – между выборками есть статистически значимые различия.

Сравнение двух массивов значений коэффициента синхронности при неправильной датировке из Нижегородской и Владимирской области показало, что по критерию Колмогорова—Смирнова данные массивы принадлежат к одному закону распределения (различия в частотах между выборками недостоверны) на уровне значимости α = 0,01.

Сравнение двух массивов значений коэффициента синхронности при неправильной датировке из Нижегородской и Вологодской области показало, что по критерию Колмогорова—Смирнова данные массивы принадлежат к одному закону распределения (различия в частотах между выборками недостоверны) на уровне значимости α = 0,01 .

Сравнение двух массивов значений коэффициента синхронности при неправильной датировке из Вологодской и Владимирской области показало, что по критерию Колмогорова—Смирнова данные массивы принадлежат к одному закону распределения (различия в частотах между выборками недостоверны) на уровне значимости α = 0,49, а, следовательно, также на стандартных уровнях значимости 0,05 или 0,01.

Подводя итог, следует заключить, что все три массива значений коэффициента синхронности при экспериментально заданной неправильной датировке согласно оценке по критерию Колмогорова—Смирнова при уровне значимости 0,01 имеют одинаковый закон распределения. Массивы значений при правильной датировке имеют разные законы распределения, что видимо, обусловлено разной ценопопуляционной структурой анализируемых популяций.

Однако, если рассматривать только два массива — из Нижнего Новгорода и Владимирской области, то они также имеют общий закон распределения при уровне значимости 0,01. Если обратиться к лесорастительному районированию С.Ф. Курнаева, то можно отметить, что исследованная вологодская популяция сосны существует в условиях подзоны средней тайги, тогда как владимирская и нижегородская — в подзоне южной тайги. Таким образом, наблюдающиеся отличия вполне объяснимы с естественно-исторических позиций. Вероятно, что природно-зональные условия оказывают влияние на генетическую структуру древостоев сосны. Можно предположить, что частота пожаров в зоне южной тайги выше, и это определяет специфику действия векторов естественного отбора в популяциях сосны между этими зонами.

С практической точки зрения важно, что массивы значений при неправильной датировке могут быть объединены в единую выборку и на ее основе выведен общий закон распределения (табл. 4). В таблице 4 представлены накопленные значения частоты встречаемости коэффициентов синхронности. На основании полученного ряда можно оценить вероятность ошибки в выводе о взаимно неверной датировке древесно-кольцевых хронологий. Вывод в полной мере справедлив для ситуации, когда эталонная хронология построена по 20 индивидуальным деревьям сосны I–III класса роста по Крафту, с каждого из которых отбиралось по 1 керну на высоте 1,3 м. Тестовая хронология строилась на основе данных одного дерева, с которого был отобран один керн на высоте 1,3 м.

Таблица 5

Значения накопленной частоты встречаемости коэффициента синхронности между эталонной и тестовой хронологией сосны обыкновенной при искусственно смоделированной неправильной датировке хронологий

Заключение

Исследование групповой изменчивости временных рядов радиального прироста по показателю синхронности представляет практический интерес для развития методик судебно-ботанической экспертизы, совершенствования их до такой степени, чтобы они стали доступны широкому кругу специалистов лесного хозяйства. В то же время подобного рода исследования представляют фундаментальный интерес с точки зрения генетики популяции лесообразующих пород и развития методов селекции на продуктивность и устойчивость. На основании полученного ряда можно оценить вероятность ошибки в выводе о взаимно неверной датировке древесно-кольцевых хронологий. Следует добавить, что перекрестная датировка в настоящее время является неотъемлемой частью любого дендрохронологического исследования. Полученные данные представляют ценность для построения сверхдолгосрочных хронологий сосны и реконструкции и прогноза частоты возникновения засух на их основе.

Работа выполнена при финансовой поддержке РНФ (грант 14-17-00645) в Институте географии РАН, Московском Государственном Университете леса и в Институте глобального климата Росгидромета и РАН.

Рецензенты:

Дроздов И.И., д.с.-х.н., профессор, профессор кафедры лесных культур и механизации лесохозяйственных работ, Московский Государственный Университет Леса, г. Москва;

Чернышенко О.В., д.б.н., профессор, зав. кафедрой декоративного растениеводства и физиологии растений, Московский Государственный Университет Леса, г. Москва.

Библиографическая ссылка