Процесс формирования покрытий в электрическом поле методом электрофореза получил достаточно широкое применение, в частности, используется как один из способов нанесения диэлектрика при производстве элементов РЭА. Одним их показателей качества диэлектрических пленок является их равномерность.
Элементы, на которые наносится диэлектрическое покрытие, имеют сложную форму и конечные размеры, что вызывает неравномерность напряженности электрического поля. В результате осаждаемое диэлектрическое покрытия получается неравномерным по толщине. Для тонких пленок, когда 10% разницы в толщине составляют десятые доли микрометра, актуальной становится задача теоретического исследования влияния формы электродов на качество покрытий.
В электрохимических методах нанесения покрытий различают действия первичного и вторичного электрических полей. Первичное поле описывается уравнениями Пуассона или Лапласа, зависит от геометрических параметров системы электродов и оказывает основное влияние на разницу в толщине. Действие вторичного тока обусловлено электрохимическими параметрами рабочей среды.
Исследование распределения первичного электрического поля и его влияния на равномерность получаемых тонкопленочных покрытий проведено для системы электродов, имеющих гребенчатую форму и применяемой при производстве стеклокерамических конденсаторов. Схема расположения электродов исследуемой системы – катод между двумя анодами. Форма зубца гребенки приведена на рисунке 1.
При отсутствии в рассматриваемой системе свободных объемных зарядов распределение потенциального электрического поля подчиняется уравнению Лапласа:
![]() , (1)
, (1)
где j(r) – функция потенциала в трехмерном точечном евклидовом пространстве (r) º (x, y, z). Уравнение Лапласа в дифференциальной форме:
![]() . (2)
. (2)
Решение уравнения Лапласа в частных производных найдено с использованием метода конечных разностей. Суть данного метода состоит в том, что совокупность значений потенциала поля находится путем замены одного описывающего поле дифференциального уравнения системой простых линейных уравнений в конечных разностях. Эти уравнения связывают значение потенциала в каждой точке со значениями потенциала в соседних точках. Разностный эквивалент уравнения Лапласа имеет вид:
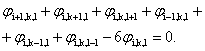 (3)
(3)
Граничные значения потенциального поля были определены из условия симметрии элементов электродной системы и равномерного распределения потенциала между электродами в местах, значительно удаленных от краев [5].
Таким образом, математическая модель рассматриваемой системы имеет вид:
![]() , (4)
, (4)
где [A] – матрица размером n ´ n, составленная из коэффициентов при неизвестных, при этом номер строки матрицы соответствует номеру узловой точки; n – количество узловых точек системы, в которых определяется значение потенциала; Φ – вектор решения; B – вектор свободных членов, заданных исходя из граничных условий.
Программная реализация модели осуществлена в системе программирования Delphi 5.0.
С использованием разработанной математической модели проведено исследование потенциального поля вблизи поверхности катода. В результате проведенных расчетов для исследуемой системы электродов было установлено:
1) максимальный разброс был определен в сечении 1-10 и 3-12 (рисунок 1);
2) неравномерность поля можно уменьшить изменением соотношения геометрических параметров системы электродов;
3) значительное увеличение межэлектродного расстояния h приведет к уменьшению напряженности поля в области катода и снижению производительности технологической операции.
Для установления близости модели реальному объекту (установление адекватности модели) поставлена серия опытов. Для оценки дисперсии воспроизводимости поставлена отдельная серия опытов. В качестве критерия оценки модели был использован коэффициент неоднородности поля, под которым понимают отношение максимальной напряженности в промежутке к средней напряженности:
![]() . (5)
. (5)
В качестве критерия оценки реального объекта был принят коэффициент неравномерности толщины тонкой пленки, под которым понимают отношение максимальной толщины пленки в рассматриваемом сечении к ее среднему значению:
![]() . (6)
. (6)
Замер толщины пленки проводился в характерных точках зубца гребенчатого электрода (рисунок 1).
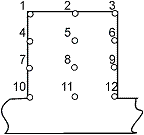
Рисунок 1. Схема расположения электродов исследуемой системы
Расчетные значения неоднородности поля и соответствующие им значения неравномерности толщины на основе экспериментальных измерений приведены в таблице 1.
Таблица 1.
|
Коэф-т неоднородности | Сечение | ||||
| 1-3 | 2-11 | 1-10 | 3-12 | 10-12 | |
| f расч. поля | 1,07 | 1,12 | 1,16 | 1,16 | 1,02 |
| f эксп. пленки | 1,06 | 1,21 | 1,29 | 1,28 | 1,04 |
Из приведенных данных видно, что неравномерность толщины наносимого покрытия соответствует расчетной неоднородности потенциального поля у поверхности заготовки электродов. Это позволяет сделать вывод о целесообразности использования предложенной модели для исследования потенциального поля и оценки такого качественного показателя как равномерность при формировании тонкопленочных диэлектриков методом электрофореза.
Библиографическая ссылка
Овчинникова Е.В. ИСПОЛЬЗОВАНИЕ МЕТОДА МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРИМЕНИТЕЛЬНО К ПРОБЛЕМЕ ОЦЕНКИ КАЧЕСТВЕННОГО ПОКАЗАТЕЛЯ ТОНКОПЛЕНОЧНОГО ДИЭЛЕКТРИКА // Современные проблемы науки и образования. 2006. № 2. ;URL: https://science-education.ru/ru/article/view?id=225 (дата обращения: 05.03.2026).



