Развитие тонкоплёночных технологий привело к прогрессу в микро- и оптоэлектронике, определяющему лицо современной информационной цивилизации. При выращивании плёнок возникает проблема построения моделей кинетики фазовых переходов первого рода в двухфазных системах.
Рассмотрим процесс образования пленки в результате газовой или жидкостной эпитаксии на кристаллической подложке. Совокупность частиц неупорядоченной фазы можно рассматривать как динамическую систему частиц, распределённых в пространстве случайным образом и находящихся в состоянии термодинамического равновесия с кристаллической подложкой. Частицы могут находиться в сколь угодно большом количестве в одном состоянии, для них не существует запрета Паули, то есть такую систему можно рассматривать как ансамбль бозе-частиц. При температурах ниже некоторой критической происходит осаждение части частиц системы на подложку в состоянии с нулевым импульсом, так называемая бозе-конденсация в поле псевдопотенциала подложки. В результате на кристаллической поверхности образуются зародыши новой фазы, происходит фазовый переход первого рода.
Несохранение числа частиц неупорядоченной системы, связанное с наличием поля подложки, приводит к появлению отличных от нуля средних ![]() , определяющих концентрацию частиц в газовой фазе, а также аномальных средних
, определяющих концентрацию частиц в газовой фазе, а также аномальных средних ![]() которые при k=0 определяют концентрацию осаждённых частиц – конденсата. Для аномальной функции Грина (ФГ)
которые при k=0 определяют концентрацию осаждённых частиц – конденсата. Для аномальной функции Грина (ФГ) ![]() получено уравнение
получено уравнение ![]() , где
, где ![]() . Здесь
. Здесь ![]() – энергия одночастичных возбуждений.
– энергия одночастичных возбуждений.
Решая совместно систему уравнений для ![]() – нормальной и аномальной ФГ находим для щели в спектре аномальной ФГ уравнение:
– нормальной и аномальной ФГ находим для щели в спектре аномальной ФГ уравнение:
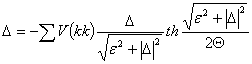 .
. ![]()
имеет смысл щели в спектре возбуждений монослоя кристаллического конденсата на подложке, преодоление которой необходимо для начала образования плёнок. Таким образом, появление ![]() является критерием начала конденсации неупорядоченной фазы на кристаллической подложке.
является критерием начала конденсации неупорядоченной фазы на кристаллической подложке.
Кроме парного взаимодействия частиц конденсата ![]() в спектре возбуждений
в спектре возбуждений ![]() содержится псевдопотенциал взаимодействия частиц конденсата с подложкой, зависящий от температуры подложки.
содержится псевдопотенциал взаимодействия частиц конденсата с подложкой, зависящий от температуры подложки.
Самоорганизация наноструктур носит пороговый характер. В докритическом режиме флуктуации затухают, а выше порога, они усиливаются и делают устойчивым новый режим, приводящий к появлению плёночных структур. Соотношение для щели даёт спинодаль появления тонких плёнок на поверхности подложки. Проведём расчёт критических температур возникновения щели в спектре возбуждений конденсата при росте пленки Zrна поверхности кристалла Zr.
Для получения фазовой диаграммы появления плёночной структуры при различных интенсивностях межатомных взаимодействий А и внутриплоскостных В построим график критической температуры в плоскости констант А и В при температуре подложки 700 К.
Рисунок 1 позволяет оценить влияние внутриплокостных и межплоскостных взаимодействий на температуру появления зародышей плёночных структур.
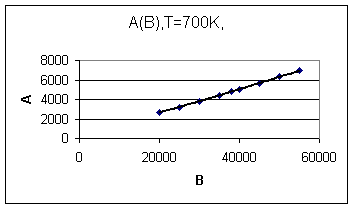
Рисунок 1. Связь критической температуры с силовыми константами
Библиографическая ссылка
Галай Е.О. КВАНТОВОСТАТИСТИЧЕСКАЯ МОДЕЛЬ ОБРАЗОВАНИЯ ПЛЁНКИ НА КРИСТАЛЛИЧЕСКОЙ ПОДЛОЖКЕ // Современные проблемы науки и образования. 2006. № 2. ;URL: https://science-education.ru/ru/article/view?id=217 (дата обращения: 05.03.2026).



