Постановка вопроса. Тема ускорения информационного поиска актуальна практически для всех существующих информационных систем [9, 10]. В качестве алгоритмической основы разработки быстродействующих систем поиска можно рассматривать разрядное распараллеливание операций сравнения слов и элементов строкового типа. С этой целью ниже излагается метод поразрядно-параллельного алгебраического сложения чисел, который не включает операций вычисления переноса, далее, излагается способ его переноса на случай поразрядно-параллельного сравнения чисел и данных строкового типа. Целью переноса является разработка основы для максимально параллельного выполнения базовых операций поиска, включая сравнение, сортировку, и распространение метода одновременно на поиск чисел и строк. Конкретной задачей излагаемого сообщения является программный эксперимент по моделированию предложенного поразрядно-параллельного сравнения элементов строкового типа для верификации разрабатываемого метода и алгоритмов на его основе. В работе приводится программа, по которой выполняется моделирование, и описываются результаты эксперимента.
Метод поразрядно-параллельного алгебраического сложения заимствуется из [1, 2]. Пусть два двоичных полинома
, 
, 
, 
, (1)
условно расположены в двух входных разрядных сетках (РС), 
и 
, номера клеток которых совпадают с индексами коэффициентов из (1).
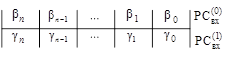. (2)
Синхронно и взаимно независимо по всем номерам разрядов 
из (2) выполняется операция 
суммирования двоичных коэффициентов равного веса по вертикали (
). Результат представляется в двоичном коде
, 
, 
. (3)
Коэффициенты из (3) располагаются по диагонали двух выходных РС, – 
и 
, образуя диагональную от j-го разряда запись (
-запись) вида
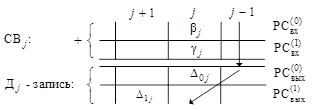. (4)
Предварительный результат сложения:
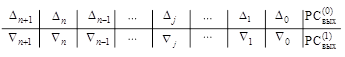, (5)
где 
, 
из (4), 
.
Все переносы в (5) оказываются взаимно отделенными вертикальными парами нулей:
, 
,
где 
, 
из (5), 
, поскольку [2] при любом из (4) складываются не более двух единиц одинакового веса. Аналогично, в (4) по диагонали – записи от 1 в 
не может располагаться 1 в 
. На этой основе корректным является следующее преобразование промежуточного набора (5). Все разряды, имеющие значение 
, из (и только из ) в (5) подвергаются тождественному преобразованию:
, 
. (6)
При этом правая часть (6) размещается в j-й клетке и в 
-й клетке в порядке 
– записи для всех номеров j преобразуемых разрядов:
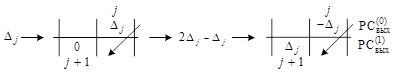(7)
Преобразование (7) корректно, поскольку в -й клетке всегда находится ноль – до применения (6) – при условии, что в , иначе – запись означала бы результат сложения трех единиц веса -го разряда, тогда как их число не больше двух [1, 2].
Вслед за тем параллельно по всем выполняется шаг вертикального сложения, результатом которого в каждом разряде всегда будет либо 0, либо 
, либо 
[1, 2]. При этом значение знакоразрядного кода расположится в, где, таким образом, сформируется окончательное значение вычисляемой суммы 
и 
из (1).
Временная сложность 
параллельного сложения в знакоразрядном коде составит 
при количестве элементов 
сумматора пропорциональном числу разрядов слагаемых:
, 
.
Сравнение двоичных чисел. Предполагается, что сравниваемые числа имеют формат (1) с нумерацией разрядов справа налево. Пусть число 
принимается за уменьшаемое, 
– за вычитаемое, тогда записывается в обратном коде (единицы заменяются нулями, нули – единицами), затем используется тождественное преобразование [6]:
, (8)
с учетом
, (9)
или, в позиционной системе,
. (10)
Над числом и числом , взятым в обратном коде, параллельно по всем номерам разрядов выполняется операция , затем и (в обратном коде) суммируются по схеме (2) – (7). Для восстановления правильного результата вычитания учитывается (8) – (10): от однорядного знакоразрядного двоичного кода полученного результата следует вычесть 
. Это равносильно тому, что с полученным результатом складывается 
– к младшему разряду добавляется 
, а к разряду веса 
добавляется 
.
Знак сравнения и определяется знаком старшего ненулевого разряда однорядного знакоразрядного двоичного числа, полученного в скорректированном окончательном результате. Если знак этого разряда отрицательный, то 
, если положительный, то 
, если все разряды нулевые, то 
.
Разрядное распараллеливание сравнения строк. Метод переносится [4, 5] на сравнение элементов строкового типа, для краткости, – строк. Все символы представляются в ASCII-коде в двоичной форме. Набор двоичных кодов всех символов строки в порядке расположения интерпретируется как единое числовое значение. Сравнение полученных двоичных кодов выполняется путем алгебраического сложения, изложенным поразрядно-параллельным способом, однако при этом, в соответствии с лексикографическим упорядочением слов, выравнивание весов разрядов выполняется по старшим разрядам, недостающие младшие разряды дополняются нулями. Например, сравниваются слова 'poisk' и 'primer'. Их двоичный код с выравниваем старших разрядов соответственно примет вид:
0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 0 0 1 1 0 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0 1 1 1 0 0 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 1 0 1 0 1 1 0 0 1 0 1 0 1 1 1 0 0 1 0
Слово «poisk» интерпретируется как уменьшаемое, «primer» – как вычитаемое. После перевода вычитаемого в обратный код алгебраическому сложению подлежат:
0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 0 0 1 1 0 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0
1 0 0 0 1 1 1 1 1 0 0 0 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 0 1 1 0 1 0 1 0 0 0 1 1 0 1
Параллельно по всем номерам разрядов выполняется операция :
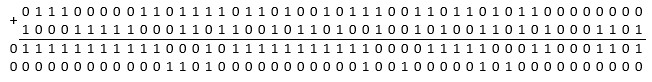
Согласно (5) – (7) выполняется преобразование:
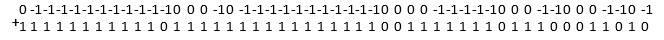
Параллельное по всем разрядам суммирование по вертикали влечет:
1 0 0 0 0 0 0 0 0 0 0 -1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 -1 0 0 1 0 -1 1 -1
Результат корректируется в соответствии (8) – (11), что влечет окончательное значение алгебраической суммы
0 0 0 0 0 0 0 0 0 0 0 -1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 -1 0 0 1 0 -1 1 0
Старший ненулевой разряд отрицателен, следовательно, первое слово лексикографически меньше второго: 'poisk' < 'primer'.
Замечание 1. Поразрядно-параллельное нахождение старшего ненулевого разряда в знакоразрядном коде – самостоятельная схемотехническая задача. Такой разряд требуется выделить программно или аппаратно, что возможно, например, при помощи схемы, представленной в [7]. Можно, с другой стороны, выделить старший ненулевой разряд аналогично нормализации мантиссы числа с плавающей точкой с помощью параллельного сдвигателя, описанного в [8]. Ниже решение этой задачи не обсуждается.
С учетом данного замечания изложенное бинарное сравнение независимо от числа разрядов занимает время одной бинарной операции над двоичными коэффициентами одного веса –
,
независимо от 
, где – число разрядов двоичного представления строки.
Программный эксперимент. Целью работы является численное моделирование изложенного метода и программный эксперимент для проверки его универсальности и достоверности. Ниже представлена консольная программа Delphi, затем описаны результаты эксперимента.
program Proverka;
{$APPTYPE CONSOLE}
uses
SysUtils;
CONST nn=100000;
S1='poisk'; S2='primer' ;
type mass=array[0..nn{*8}] of Integer;
var
a,b,a1,b1,a4,b4, a2,b2,a3,b3:mass;
s3:string;
cod,ii,y,n,m,i,k:integer;
function IntToBin(x:LongInt):string;
varres:string;
begin
RES:='';
while x<>0 doBegin
if (x mod 2=0) then res:='0'+res else res:='1'+res;
x:=x div 2; end;
while (Length(Res)<>8) do res:='0'+res;
IntToBin:=Res;
end;
procedure Assc(c:string;nm:Integer; var x:mass);
beginfor i:=1 to nm do x[i]:=Ord(c[i]);end;
procedure Assctobin(x: mass;nm:Integer; var x1:mass);
beginy:=1;
for i:=1 to n do
begin
s3:=inttobin(x[i]);
for ii:=1 to 8 dobegin
val(s3[ii],x1[y],cod);y:=y+1;end;
end;
end;
procedure srav(varx,y:mass;nm:Integer; varxr,yr:mass);
var i:integer;
begin
for i:=1 to nm*8 do
if y[i]=1 then y[i]:=0 else y[i]:=1; writeln; writeln;
for i:=1 to nm*8 do
if (x[i]=1) and (y[i]=1) then
begin a2[i]:=0;b2[i-1]:=1; end
else a2[i]:=a1[i]+b1[i];
Writeln ('massiv a2 i b2');
for i:=1 to n*8 do write(a2[i]:5);writeln;writeln;
for i:=1 to n*8 do write(b2[i]:5);writeln; writeln;
for i:=0 to nm*8 do
if (a2[i]=1) then a3[i]:=-1 else a3[i]:=a3[i];
for i:=0 to nm*8 dobegin b3[i]:=b2[i];
if (a3[i]=-1) then b3[i-1]:=1; end;
Writeln ('massiv a3 i b3');
for i:=1 to n*8 do write(a3[i]:5); writeln; writeln;
for i:=1 to n*8 do write(b3[i]:5);writeln; writeln;
for i:=0 to n*8 do
if (a3[i]=1) and (b3[i]=1) then
beginxr[i]:=0;yr[i-1]:=1;end
elsexr[i]:=a3[i]+b3[i];
xr[0]:= xr[0]-1;xr[nm*8]:=xr[nm*8]+1;end;
begin
n:=length(s1); m:=length(s2);
Assc(s1,n,a); Assc(s2,m,b);
writeln ('assci-kodeslova 1');
for i:=1 to n do write(a[i]:5);writeln;writeln;
writeln ('massiv b ');
for i:=1 to m do write(b[i]:5); Writeln; Writeln;
Assctobin(a,n,a1);Assctobin(b,m,b1);
if m>n then n:=m;
Writeln ('massiv a1 i b1');
for i:=1 to n*8 do write(a1[i]:5);writeln;writeln;
for i:=1 to n*8 do write(b1[i]:5); writeln; writeln;
srav(a1,b1,n,a4,b4);
Writeln ('massiv a4 i b4');
for i:=0 to n*8 dowrite(a4[i]:5); writeln; writeln;
for i:=0 to n*8 do write(b4[i]:5); writeln; writeln;
i:=0;
while (a4[i]=0)and (i<>n*8) do i:=i+1;
if a4[i]<0 then writeln ('1<2') else
if a4[i]>0 then writeln ('1>2')else writeln ('1=2');
Readln;
Readln;
{ TODO -oUser -cConsole Main : Insert code here }
end.
1. На вход программы были поданы 2 предложения S1 и S2.
S1='Уже было начало июня, когда князь Андрей, возвращаясь домой, въехал опять в ту березовую рощу, в которой этот старый, корявый дуб так странно и памятно поразил его.'
S2='Уже было начало июня, когда, возвращаясь домой, мы въехали в березовую рощу.'
В результате работы программы был получен верный результат сравнения: S1< S2.
2. Если в этих же исследуемых строках удалить все знаки препинания, то получится другой, но также верный результат: S1> S2.
3. В следующем примере в сравнении рассматривается только фрагменты строк, сформированные следующим образом:
t:=pos('мой',s1);
s11:=copy(s1,t,6);
writeln(s11);
t:=pos('мой',s2);
s22:=copy(s2,t,6);
S1='Уже было начало июня, когда князь Андрей, возвращаясь домой, въехал опять в ту березовую рощу, в которой этот старый, корявый дуб так странно и памятно поразил его.';
S2='Уже было начало июня, когда возвращаясь домой, въехали в березовую рощу.';
Таким образом, на вход программы для сравнения были поданы следующие фрагменты строк:
S11 ='мой, в'
S22='мой, в'
ASCII-код символов S11: 236 238 233 44 32 226
ASCII-код символов S22:236 238 233 44 32 226
Соответственные двоичные формы ASCII-кодов:
1 1 1 0 1 1 0 0 1 1 1 0 1 1 1 0 1 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 0
1 1 1 0 1 1 0 0 1 1 1 0 1 1 1 0 1 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 0
С представлением вычитаемого в обратном коде получится:
1 1 1 0 1 1 0 0 1 1 1 0 1 1 1 0 1 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 0
0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 1 0 0 0 1 0 1 1 0 1 1 0 1 0 0 1 1 1 1 0 1 1 1 1 1 0 0 0 1 1 1 0 1
Представление промежуточной суммы:
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Преобразование (6), (7) влечет:
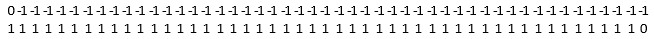
Результат поразрядно-параллельного выполнения :
Коррекция суммы в соответствии с формулами (8), (9):
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Таким образом, сравниваемые элементы строк равны между собой: S11=S22.
4. Метод непосредственно применим для сравнения целых чисел с тем изменением, что сравниваемые числа выравниваются по младшему разряду.
Например, представленная программа выдаст сравнение строковых констант '16' и '24': S1<S2.
5. При сравнении целых чисел разной разрядности следует предварительно дополнить меньшее число предшествующими незначимыми нулями. Так, для сравнения чисел 160 и 24 они предварительно должны быть преобразованы в строки вида '160' и '024'.
6. С выравниванием порядков эта схема переносится на сравнение вещественных чисел с плавающей точкой. В этом случае представленная программа выдаёт: '16.05'>'16.03', '16.005'<'17.003', '016.050'<'170.003'.
Во всех вариантах эксперимента данная программная модель давала правильные результаты поразрядно-параллельных сравнений чисел и слов.
В [3] приводится близкий к изложенному способ, при этом он непосредственно объединяет поиск чисел и слов. В файле при помощи сортировки ищутся абсолютные величины разностей ASCII-кодов строк или их элементов, аbs (ord()-ord()), или непосредственно разности чисел в формате представления языка программирования, аbs (х-у). Нулевое значение разности, в последнем случае с точностью до приближения, означает искомое значение. С выравниванием порядков эти операции осуществимы поразрядно-параллельным способом, отсюда на изложенной основе возможно объединение операций поиска чисел с плавающей точкой и элементов строкового типа.
Заключение. В статье представлен метод разрядного распараллеливания операции сравнения для информационного поиска. Метод основан на бинарном алгебраическом сложении полноразрядных чисел без вычислений переноса. Указаны особенности применения метода к поразрядно-параллельному сравнению чисел и строк. Основное содержание статьи составляет программная модель выполнения операций сравнения на основе данного метода и описание результатов программного эксперимента. Эксперимент подтверждает достоверность метода и правильность работы предложенных алгоритмов.
Рецензенты:
Боженюк А.В., д.т.н., профессор кафедры информационно аналитических систем безопасности Инженерно-технологическая академия Южного федерального университета, г. Таганрог;
Карелин В.П., д.т.н., профессор, заведующий кафедрой прикладной математики и информационных технологий Таганрогского института управления и экономики, г. Таганрог.
Библиографическая ссылка
Ромм Я.Е., Белоконова С.С. МОДЕЛИРОВАНИЕ РАЗРЯДНОГО РАСПАРАЛЛЕЛИВАНИЯ СРАВНЕНИЙ СТРОКОВЫХ И ЧИСЛОВЫХ ЭЛЕМЕНТОВ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=21302 (дата обращения: 21.05.2025).