Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Акишкин В.Г. 1 Набиев Р.А. 1 Путина С.А. 1

---

1 Астраханский Государственный Технический Университет

В статье рассмотрены особенности методики контроллинга территориальных программ государственных гарантий бесплатной медицинской помощи. В современных условиях российской экономики, классические экономические инструменты и методы, построенные на линейных равновесных моделях, оказались малопродуктивными. Это в полной мере относится и к системе российского здравоохранения, находящейся в стадии глобальной реформации, перехода на новую усложненную структурную основу. В данной связи авторами статьи предлагается использование методов нелинейной динамики, в частности элементов фрактальной статистики и математики в целях разработки эффективной методики осуществления контрольной деятельности в сфере здравоохранения. Предложенная методика контроллинга территориальных программ государственных гарантий является интуитивно понятным визуальным инструментом, позволяющим оперативно отслеживать правильность параметров запрашиваемых субъектами объемов финансирования территориальных программ государственных гарантий.

Статья в формате PDF

286 KB

мониторинг

контроллинг

здравоохранение

программы государственных гарантий

методы нелинейной динамики

1. Арсаханова З.А., Султанов Г.С. Особенности формирования региональных бюджетов субъектов СКФО // Экономика и предпринимательство. - 2013. - 12-2 (41-2). - С. 309-313.

2. Ганюкова Н.П. Фрактальный анализ как инструмент контроля бюджетной политики внутриструктурных подразделений государственных учреждений / Ганюкова Н.П., Набиев Р.А., Муц В.Н. // Бизнес. Образование. Право. Вестник Волгоградского института бизнеса. - 2013. - № 4 (25). - С. 178-183.

3. Кучеренко В.З. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие. - М. : ГЭОТАР-МЕДИА, 2004. – 192 с.

4. Перепелица В.А. Исследование R/S-траектории одного временного ряда страхования // Исследовано в России: электронный журнал. - 248. – 2004. http://zhurnal.ape.relarn.ru/articles/2004/248.pdf

5. Перепелица В.А., Тамбиева Д.А. Системы с иерархической структурой управления: разработка экономико-математических и инструментальных методов. - М.: Финансы и статистика, 2009. – 270 с.

В настоящий момент современная российская система здравоохранения вступила в новый цикл своего развития. Это связано с глобальной реформацией, переходом на новую структурную основу, ее усложнением, а также с вторжением в науку управления элементами системы здравоохранения «математических методов нелинейной динамики» [1; 2]. Важнейшей предпосылкой такого преобразования является появление новейших компьютерных технологий, которые дают возможность исследовать, контролировать и прогнозировать сложные явления и процессы путем визуализации.

Практика показала, что в современных условиях российской экономики с относительно частыми финансовыми кризисами классические экономические инструменты и методы, построенные на линейных равновесных моделях [3], оказались малопродуктивными. В связи с чем нами предлагается использование методов нелинейной динамики, а в частности элементов фрактальной статистики и математики в целях разработки эффективного инструмента осуществления контрольной деятельности.

Имитационное и математическое моделирование различных процессов и систем, присутствующих в сложных системах управления, показало, что их поведение определяется конечным числом параметров порядка, то есть от бесконечного, слабо формализованного множества значений наблюдаемых состояний и функций можно перейти к конечному, а чаще к небольшому числу значимых переменных или параметров.

Данный подход является релевантным в случаях, когда нет необходимости четкой фиксации значений переменных, но необходимо получить статистические данные для проведения обзорного анализа. С целью перехода к конечному числу анализируемых значимых параметров программы государственных гарантий оказания бесплатной медицинской помощи (ПГГ) агрегируем имеющиеся показатели, разделив их по характеру предоставляемой информации на стоимостные (NCi) и объемные (NVi) нормативы. Классификация представлена в таблице 1.

Таблица 1

Классификация нормативов

Источник: составлено авторами.

Для реализации аналитического инструментария, позволяющего контролировать выполнение политики субъекта Федерации в области здравоохранения, введем понятие контрольных индикаторов INC и INV, значения которых станут сигналом, характеризующим выполнение тем или иным субъектом РФ программы госгарантий в сфере здравоохранения.

INC = φρ {NC1, NC2 ,….. NC10}

INV = φρ {NV1, NV2 ,….. NV4}, (1)

где INC – индикатор стоимостных нормативов, а INV - индикатор объемных нормативов, φρ – фазовое пространство.

Методика контроллинга реализации политики субъекта Российской Федерации и страны в целом в области охраны здоровья использует математические модели теории самоподобия фракталов. Данные модели позволяют с помощью построения фазовых портретов оценить тренд с целью проверки гипотезы о наличии фрактального «подобия» сравниваемых параметров ПГГ и ТПГГ. В основе данной гипотезы о «подобии» лежит предположение, что структуры программ всегда идентичны.

Структура ПГГ представлена как двухуровневая иерархическая система, нижний уровень которой включает множество элементов (значений нормативов территориальной программы государственных гарантий (ТПГГ)), а верхний уровень – совокупность кластеров (целевых значений нормативов ПГГ). С целью достижения трендового фрактального соответствия целевой ПГГ кластеры контролируемой ТПГГ должны обладать «фрактальным подобием», то есть иметь одинаковый тренд при сравнении с аналогичными кластерами целевой ПГГ. Предлагается при проведении мониторинга исследовать наличие одинакового фрактального тренда фазовых портретов у объемных и стоимостных нормативов в отдельности [4; 5].

Схема трендового фрактального подобия кластеров ПГГ и ТПГГ в разрезе стоимостных и объемных нормативов представлена на рисунке 1.

Рассмотрим процесс построения фазовых портретов с целью проверки гипотезы о наличии трендового фрактального «подобия» сравниваемых нормативов ТПГГ и целевой ПГГ.

Для примера возьмем по два ряда сформированных из объемных и стоимостных нормативов за 2014 год двух субъектов РФ - Астраханской и Волгоградской областей, сравнив их с целевыми значениями нормативов.

Набор анализируемых рядов стоимостных нормативов:

- соответствующий ряд стоимостных нормативов целевой ПГГ обозначен как: NC¹ = {nc_i¹}, i=1,2,...,n;

- соответствующий ряд стоимостных нормативов ТПГГ Астраханской области: NС² = {nс_i²}, i=1,2,...,n;

соответствующий ряд стоимостных нормативов ТПГГ Волгоградской области: NС³ = {nс_i³}, i=1,2,...,n; где nс_i ^r - числовое значение i-го норматива для NС^r, .

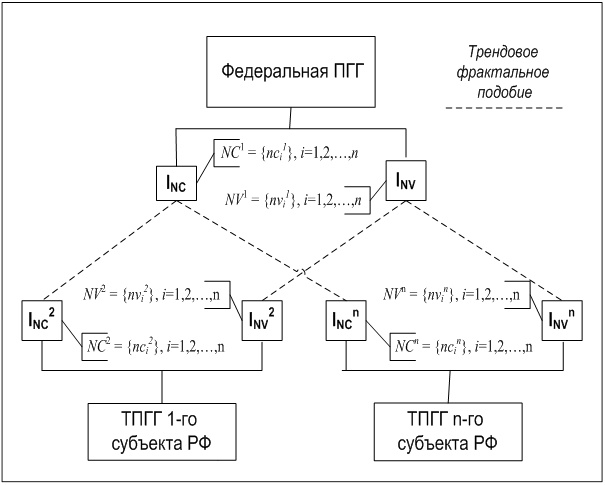
Рис. 1. Фрактальное подобие между кластерами ПГГ различных уровней.

Числовые значения стоимостных нормативов в тысячах рублей сравниваемых рядов представлены в таблице 2.

Таблица 2

Числовые значения стоимостных нормативов

Набор анализируемых рядов объемных нормативов:

- соответствующий ряд объемных нормативов целевой ПГГ обозначен как: NV¹ = {nv_i¹}, i=1,2,...,n;

- соответствующий ряд объемных нормативов ТПГГ Астраханской области: NV² = {nv_i²}, i=1,2,...,n;

соответствующий ряд объемных нормативов ТПГГ Волгоградской области: NV³ = {nv_i³}, i=1,2,...,n; где nv_i ^r - числовое значение i-го норматива для NV^r, .

Числовые значения объемных нормативов в единицах сравниваемых рядов представлены в таблице 3.

Таблица 3

Числовые значения объемных нормативов

К представленным рядам применим фрактальный фазовый анализ, основой которого является исследование фазовых портретов, выделение в них квазициклов, определение и сравнение длин выделенных квазициклов. В качестве фазовых пространств φρ применим простейшие варианты следующего вида:

φ2(NC)={(nci, nci+1)}, i=1,2,…,n-1 - для стоимостных нормативов;

φ2(NV)={(nvi, nvi+1)}, i=1,2,…,n-1 - для объемных нормативов.

Размерность фазового пространства определяется как С=2-Н [3]. Для исследуемых временных рядов , следовательно С<2, в связи с чем построим φρ (NC) и φρ (NV) размерности ρ=2. Сравнительные фазовые портреты для стоимостных показателей федеральной ПГГ и ТПГГ Астраханской области (2а, 3а), а также федеральной ПГГ и ТПГГ Волгоградской области (2б, 3б) представлены на рисунках 2 и 3.

Выделим квазициклы в представленных рядах. Подпоследовательность точек (NC_i,nc_i+1,...,nc_i+k) последовательности (NC₁,NC₂,...,NC_n-1) ∈ φ₂(NC) в фазовом пространстве φ_ρ(NC) размерности ρ=2 ((NC_i,NC_i+1,...,NC_i+k) ⊂(NC₁,NC₂,...,NC_n) образует квазицикл в случае выполнения одного из двух условий:

на интервале [NCi,NCi+k] отрезки (NCi,NCi+1) и (NCi+k-1,NCi+k) образуют первое на данном интервале самопересечение фазовой траектории;

в случае отсутствия самопересечения на интервале [NCi,NCi+k+1] и расхождении фазовой траектории концом квазицикла считаем точку NCi+k, расстояние от которой до точки NCi на интервале [NCi,NCi+k+1] является наименьшим, т.е.:

Длиной выделенного квазицикла является величина k+1.

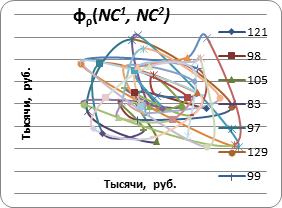а

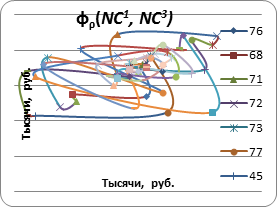б

Рис. 2. Сравнительные фазовые портреты стоимостных нормативов ПГГ и ТПГГ субъектов.

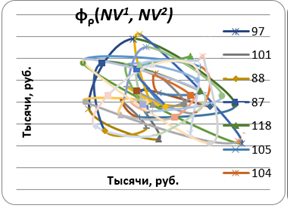
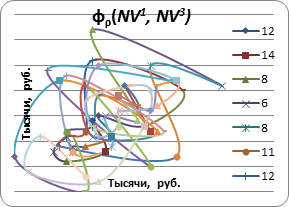
Рис. 3. Сравнительные фазовые портреты объемных нормативов ПГГ и ТПГГ субъектов.

Следующим этапом, с целью проведения сравнительного фрактального анализа фазовых портретов, необходимо определить параметры:

p - длина квазицикла; h^r_p - частота появления квазицикла длины p (в процентном выражении) в рядах параметров NC^{r b} и NV^r, где r - номер исследуемого ряда для R/S-анализа; q^r_p - частота появления квазицикла длины p (в процентном выражении) в рядах параметров NC^{r b} и NV^r, для фазового анализа.

Для имеющихся рядов рассмотрим статистику пар, полученных в результате последовательного R/S-анализа (p,h¹_p), (p,h²_p) и (p,h³_p). Процентное соотношение длин выделенных квазициклов рядов NC¹, NC², NC³ в табличном виде представлено в таблице 4.

Таблица 4

Сводное представление результатов R/S-анализа

Сравним статистику пар, полученных с помощью фазового анализа (p,q¹_p), (p,q²_p) и (p,q³_p). Сводная таблица процентного соотношения длин выделенных квазициклов рядов NC¹, NC² и NC³ представлена в таблице 5.

Таблица 5

Сводное представление результатов фазового анализа

В результате применения последовательного R/S-анализа и фазового анализа наибольший процент квазициклов для NC1 и NC2 соответствуют квазициклам длины 8, а для NC3 – длины 4. Аналогично проведем анализ трендового фрактального подобия для объемных нормативов NV1, NV2 и NV3. Результаты анализа представлены в таблицах 6 и 7 соответственно.

Таблица 6

Сводное представление результатов R/S-анализа

Таблица 7

Сводное представление результатов фазового анализа

В результате применения последовательного R/S-анализа и фазового анализа наибольший процент квазициклов для NC¹ равен 6, для NC² наибольшие значения соответствуют квазициклам длины 7, а для NC³ - длины 4.

Таким образом, на основе полученных данных можно сделать вывод о наличии трендового фрактального «подобия» между значениями стоимостных нормативов рядов NC¹ и NC², но объемные показатели различны по тренду. Для NC¹ и NC³ трендовое фрактальное подобие отсутствует в обоих случаях. Следовательно, можно говорить об отсутствии требуемого стратегического соответствия исследуемых ТПГГ.

Предложенная методика контроллинга территориальных ПГГ является интуитивно понятным визуальным инструментом, позволяющим оперативно отслеживать правильность параметров запрашиваемых субъектами объемов финансирования ТПГГ.

Рецензенты:

Абдулгалимов А.М., д.э.н., профессор, профессор кафедры «Налоги, денежное обращение» ФГБОУ ВПО «Дагестанский государственный университет», г. Махачкала;

Минева О.К., д.э.н., профессор, профессор кафедры «Менеджмент» ФГБОУ ВПО «Астраханский государственный технический университет», г. Астрахань.

Библиографическая ссылка