Определение миграции населения как территориального перемещения отдельных индивидов в границах одного экономического региона или за его пределы, отвлеченное от причинно-следственной связи между перемещениями дает возможность рассматривать миграцию как случайный процесс [1]. Закономерности поведения отдельных индивидов проявляются в виде тенденций, свойственных всему процессу и постоянно нарушаемых воздействием случайных факторов. Это обусловливает возможность применения вероятностных подходов к моделированию миграции[3].
Пусть имеется m населенных пунктов, между которыми происходит миграция населения. Допустим, что процесс миграции является дискретным случайным процессом марковского типа (цепью Маркова), который обозначим x(t). В каждый дискретный момент времени t процесс принимает одно из значений 1, 2, …, m, т.е. ![]() - в момент времени t = n случайный процесс принял значение i (i = 1, 2, …, m), совпадающее с номером i одного из m – населенных пунктов. Таким образом, случайное событие
- в момент времени t = n случайный процесс принял значение i (i = 1, 2, …, m), совпадающее с номером i одного из m – населенных пунктов. Таким образом, случайное событие ![]() означает, что в момент времени t = n, (n = 1, 2, …), в населенном пункте с номером i наблюдается приток мигрантов. Обозначим через
означает, что в момент времени t = n, (n = 1, 2, …), в населенном пункте с номером i наблюдается приток мигрантов. Обозначим через
![]() (j=1, …, m) - вероятность перехода процесса x(t) из состояния i, в котором процесс x(t) находился в момент t-1, в состояние j в последующий момент времени t. Эта вероятность интерпретируется как вероятность того, что в момент времени t = n в населенном пункте j будет наблюдаться приток мигрантов, если в момент t-1 = n-1 приток мигрантов наблюдается в населенном пункте i. Согласно [1]
(j=1, …, m) - вероятность перехода процесса x(t) из состояния i, в котором процесс x(t) находился в момент t-1, в состояние j в последующий момент времени t. Эта вероятность интерпретируется как вероятность того, что в момент времени t = n в населенном пункте j будет наблюдаться приток мигрантов, если в момент t-1 = n-1 приток мигрантов наблюдается в населенном пункте i. Согласно [1] ![]() определяется соотношением:
определяется соотношением:
![]() , (1)
, (1)
где ![]() - население в пункте с номером i,
- население в пункте с номером i, ![]() - миграционный поток из пункта i в пункт j в момент времени t. Предположим, что
- миграционный поток из пункта i в пункт j в момент времени t. Предположим, что ![]() известно в каждый момент времени t. Для вычисления
известно в каждый момент времени t. Для вычисления ![]() предлагается использовать кинетическое уравнение, построенное далее. Если цепь Маркова является однородной, то население
предлагается использовать кинетическое уравнение, построенное далее. Если цепь Маркова является однородной, то население ![]() - считаем постоянным.
- считаем постоянным.
Миграционный поток можно определить из следующих соображений. Пусть ![]() ,
, ![]() - коэффициенты интенсивностей миграций всех выделенных групп населения;
- коэффициенты интенсивностей миграций всех выделенных групп населения; ![]() - время приживаемости, которое определяется минимальным временем проживания в районе q, после которого миграционные параметры некоренного жителя – выходца из района
- время приживаемости, которое определяется минимальным временем проживания в районе q, после которого миграционные параметры некоренного жителя – выходца из района ![]() совпадают с миграционными параметрами коренных жителей района проживания q;
совпадают с миграционными параметрами коренных жителей района проживания q; ![]() - распределение по районам вселения для всех групп коренного и некоренного населения (этот параметр распределения по районам вселения представляет собой долю людей, выезжающих из состава коренного населения района q в район
- распределение по районам вселения для всех групп коренного и некоренного населения (этот параметр распределения по районам вселения представляет собой долю людей, выезжающих из состава коренного населения района q в район ![]() , среди всех выезжающих из этого населения в момент времени t);
, среди всех выезжающих из этого населения в момент времени t); ![]() - миграционная подвижность коренного населения возраста х, пола р, проживающего в районе q в момент времени t.
- миграционная подвижность коренного населения возраста х, пола р, проживающего в районе q в момент времени t.
Тогда ![]() определяется из соотношения [2]:
определяется из соотношения [2]:
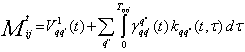 , (2)
, (2)
которое описывают миграционные потоки из района в район. Зная плотности переходных вероятностей ![]() , можно найти численность населения
, можно найти численность населения ![]() по
по ![]() из соотношения
из соотношения ![]() (Р – матрица переходных состояний). Если цепь является однородной, то последнее соотношение принимает вид
(Р – матрица переходных состояний). Если цепь является однородной, то последнее соотношение принимает вид
![]() . (3)
. (3)
С помощью математической модели (2) может быть построено распределение
![]() для использования в краткосрочных прогнозах. Качественная интерпретация полученных результатов может быть сформулирована в терминах цепей Маркова.
для использования в краткосрочных прогнозах. Качественная интерпретация полученных результатов может быть сформулирована в терминах цепей Маркова.
Таким образом, соотношения (1-3) позволяют математически обоснованно прогнозировать тенденции развития миграции при условии известности означенных выше характеристик миграционного процесса.
СПИСОК ЛИТЕРАТУРЫ
1. Денисенков М.Б., Ионцев В.А., Хореев Б.С. Миграциология.- М., 1989 г.;
2. Зуев Г.М., Сороко Е.Л. Математическое описание миграционных процессов. – Автоматика и телемеханика, 1978, №7, с. 94 -101;
3. Соболева С.В. Демографические процессы в региональном социально-экономическом аспекте. – Новосибирск: Наука. Сиб. отд-ие, 1988 г.
Библиографическая ссылка
Семенчин Е.А., Бабченко О.В. ПРИМЕНЕНИЕ ЦЕПЕЙ МАРКОВА ДЛЯ ПРОГНОЗИРОВАНИЯ МИГРАЦИОННЫХ ПРОЦЕССОВ // Современные проблемы науки и образования. 2006. № 2. ;URL: https://science-education.ru/ru/article/view?id=210 (дата обращения: 05.03.2026).



