В предлагаемой статье хотим поделиться опытом организации исследовательской работы при изучении модуля «Тени в ортогональных проекциях». В качестве задания по этому модулю студенты строят тени на нескольких фрагментах архитектурных форм. Рассмотрим пару примеров.
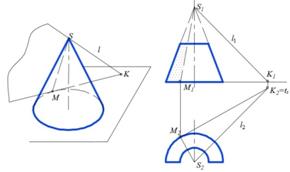
Пример 1. Дана круглая полуротонда с колоннами и открытым верхом (рис.1). Она примыкает к полуцилиндрической нише в стене.
Задача. Представить всевозможные варианты построения теней. Дать их сравнительную характеристику. Рекомендовать наиболее рациональный приём.
Остановимся на одном элементе фрагмента. Рассмотрим построение тенина антаблементе, падающей от дуги окружностиверхней плиты на нижнюю цилиндрическую поверхность.
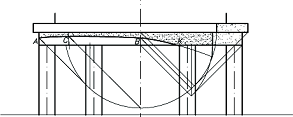
На рис. 1, а тень построена способом выноса. Вынос – это расстояние от точки до плоскости или поверхности, на которую падает тень. Строим тень, падающую на осевую плоскость от верхней и нижней дуг окружностей, выбирая на них точки, вынос которых можно определить без плана. Затем тень от верхней части преломляем на нижнюю. При этом учитываем, что на очерке и на оси контур падающей тени имеет точки (А и В) одного уровня, а высшая его точка (С) определяется при помощи конуса с углом 35°. Точка исчезновения (К) определяется обратным лучом, проведенным из точки tk пересечения теней, падающих от обеих поверхностей на осевую плоскость.
На рисунке 1, б та же тень построена при помощи биссекторного экрана. Биссекторный экран это плоскость, проходящая через ось цилиндра под углом 45° к фронтальной плоскости. На экран строим тень от верхней окружности (это будет окружность радиусом равным 0,6 R), и от образующих цилиндра. Образующие берем такие, для которых положение самих образующих и их теней можно определить по одной проекции. Затем обратными лучами переносим точки пересечения теней на соответствующую образующую.
На
рис. 1, в та же тень построена
методом лучевых сечений. На верхней окружности можно брать любые точки,
проводить лучи до пересечения с нижним цилиндром и переносить точки на фасад.
Но разумнее и рациональнее при помощи обратных лучей определить те точки
верхнего контура, которые помогут определить положение характерных точек
А, В, С и К.
Контур падающей тени во всех трёх случаях получится один и тот же.
Cравним эти три способа.
а б в
Рис. 1. Построение падающей на антаблемент тени способом: а) выноса, б) биссекторного экрана, в) лучевых сечений
Конечно, удобнее строить тень по одной проекции, так как решение занимает меньше места и получается более компактным. С этой точки зрения выигрышными являются варианты а) и б). Если тень строить только на балке, то менее загруженным построениями является вариант б). Но в этом случае для построения тени, падающей на стену надо использовать какой-то дополнительный способ. Тогда предпочтительнее будет вариант а). При наличии двух проекций лучше воспользоваться вариантом в), не забывая про характерные точки. В будущей профессиональной деятельности эти рекомендации могут пригодиться.
Тени студенты строят на всём фрагменте, а исследуют наиболее многовариантный его элемент.
Пример 2. Дана полуцилиндрическая ниша с полуконическим куполом и полуцилиндрическим фонарём.
Задача. Провести параллель между позиционными задачами и приёмами построения теней.
При выполнении задания сложный архитектурный фрагмент разбивается на простейшие элементы и на каждом из них последовательно строят тени. Рассмотрим несколько элементов, объясняя одни и то же построения двумя разными подходами к их выполнению.
Элемент 1. Полуконический купол. Построить контур собственной тени (рис. 2, а).
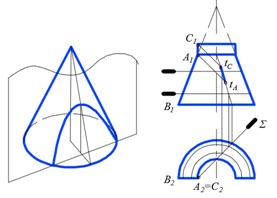
На рис. 2, а слева показано построение собственной тени конуса в аксонометрии, справа – на полуконическом куполе в ортогональных проекциях. Объясним приведённые построения.
Позиционная задача. Через вершину S и прямую l (световой луч) проводим плоскость, касающуюся поверхности конуса. Для этого строим точку К пересечения l с плоскостью основания конуса и проводим след KM касательной плоскости. Контур собственной тени купола совпадает с линией касания.
Теория теней. Строим тень от вершины S конуса на плоскость его основания: tS≡ К. Из полученной точки проводим луч, касающийся основания конуса. Образующая SM, проходящая через точку касания M, является контуром собственной тени конуса.
|
|
|
|
а |
б |
Рис. 2. Построение теней полуконического купола: а) собственной, б) падающей
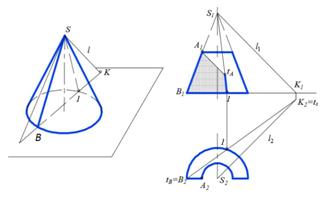
Элемент 2. Построить тень, падающую на внутреннюю поверхность купола от образующей ВS (рис. 2, б).
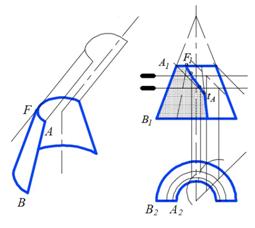
На рис. 2, б слева представлена геометрическая суть построения тени, падающей на внутреннюю поверхность конуса, справа – построение этой тени в ортогональных проекциях.
Позиционная задача. Образующая BS и световой луч l образуют плоскость Σ общего положения. Строим линию пересечения её с поверхностью конуса. Так как плоскость Σ проходит через вершину конуса, то она пересечет его по образующей. Находим прямую BK пересечения Σ с плоскостью основания конуса. Искомая образующая пройдет через вершину Sи точку 1. Нижняя её часть (от точкиtA) будет падающей тенью (рис. 2, б справа).
Теория теней. Строим тень KtB ≡ BKобразующейBS на плоскость основания конуса и отмечаем точку 1 их пересечения. Падающая тень от AB пойдет по образующей 1S в нижней её части (рис. 2, б справа).
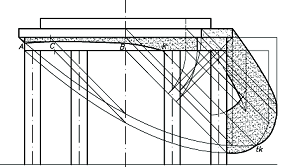
Элемент 3. Построить тень, падающую от образующей AC цилиндрического фонаря на внутреннюю поверхность купола (рис. 3, а).
Поскольку образующая цилиндрического фонаря перпендикулярна плоскости p2, то проходящая через неё плоскость Σ будет горизонтально проецирующей. На рис. 3, а слева показано, что в сечении такой плоскостью поверхности конуса получается гипербола.
Позиционная задача. Строим линию пересечения проецирующей плоскости Σ с конусом. Задачу решаем методом вспомогательных секущих плоскостей. Пересекаем конус горизонтальными плоскостями. Отмечаем точки пересечения полученных сечений со следом плоскости Σ и переносим их на фронтальную проекцию. Тень tAtC пойдёт по дуге гиперболы (рис. 3,.а справа).
Теория теней. Тень строим методом лучевых сечений. Проводим проекции нескольких окружностей, лежащих на поверхности конуса. Отмечаем точки пересечения их со световым лучом, через который проведена горизонтально проецирующая плоскость Σ. Контур падающей тени tAtC будет принадлежать дуге гиперболы, проведённой через отмеченные точки (рис. 3, а справа).
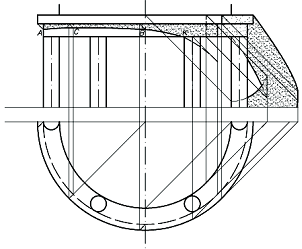
Элемент 4. Построить тень, падающую от полуокружности (нижней части кромки фонаря) на внутреннюю поверхность купола (рис. 3, б).
Тень будет давать дуга AF, ограничивающая контур собственной тени конуса.
а б
Рис. 3. Построение падающих теней на внутренней поверхности конической ниши: а) от отрезка AC, б) от дуги AF полуокружности
Геометрическим множеством всех световых лучей, проходящих через точки окружности верхнего основания конуса (она же нижняя часть кромки фонаря) является наклонный цилиндр, ось которого параллельна световому лучу (рис. 3, б слева).
Позиционная задача. Строим линию пересечения двух поверхностей: конуса и наклонного цилиндра, образованного световыми лучами. Задачу решаем методом вспомогательных секущих плоскостей. Проводим горизонтальные плоскости и строим окружности, по которым они пересекают конус и цилиндр. Отмечаем точки пересечения этих окружностей. Через них и пойдет контур падающей тени (рис. 3, б справа).
Теория теней. Задачу решаем методом горизонтальных экранов. Выбираем экран, строим линию пересечения им конуса. Строим тень от полуокружности на этот экран. Для этого находим тень от центра окружности на плоскость экрана и из полученной точки проводим дугу окружности. При пересечении тени и сечения получаем точки искомого контура падающей тени (рис. 3, б справа).
Аналогичные параллели можно провести при построении любой тени.
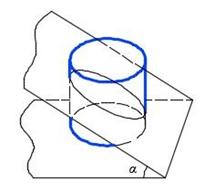
Из приведенных выше примеров видно, что одно и то же решение можно объяснить и с точки зрения позиционных задач, и с точки зрения теории теней. Видим, что по разному названные методы (как например: метод вспомогательных секущих плоскостей и метод горизонтальных экранов) имеют одну и ту же суть. Можно сказать, что геометрической основой построения теней являются позиционные задачи. Поэтому теорию теней следует рассматривать как практическое приложение позиционных задач начертательной геометрии. Это делает предсказуемым форму контура теней, что позволяет построить их с проведением небольшого количества световых лучей. Так, например, известно, что если цилиндр пересечь плоскостью, проходящей под произвольным углом к его образующим, то в сечении получим эллипс (рис. 4, а). Если же этот угол будет равен 45o, то получим окружность (рис. 4, б).
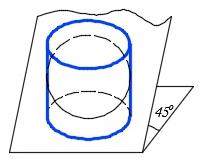
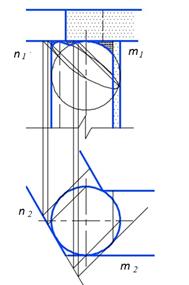
а б в
Рис. 4. Сечение цилиндра плоскостью, проходящей к образующим: а) под произвольным углом α, б) под углом 45o; в) форма теней, падающих от верхних рёбер на круглую колонну
Теперь несложно представить и форму контура тени, падающей на цилиндрическую колонну от горизонтальных ребер m и n верхней конструкции (рис. 4, в). Ребро m расположено параллельно фронтальной плоскости проекций. Следовательно, плоскость, заданная этим ребром и световым лучом проходит под углом 45o к образующим цилиндра. Тень от ребра имеет форму окружности. Ребро n не параллельно фронтальной плоскости. Поэтому тень от него имеет форму эллипса. Для его построения достаточно найти характерные точки. Отсюда вытекает и закономерность: контур тени от горизонтальной прямой на поверхность, образующие которой вертикальны, повторяет контур нормального сечения поверхности, повернутого кверху.
Из всего сказанного можно сделать вывод. Чтобы свободно разбираться в тенях, необходимо прочно усвоить базовый раздел начертательной геометрии.
Вывод. Задачи подобного рода исключают механический подход к выполнению задания. Студенту приходится анализировать и сравнивать между собою различные приёмы построения для выбора наиболее оптимального варианта. Тем самым он приобретает первый навык исследовательской деятельности. Причинно-следственную связь, установленную между различными разделами дисциплины, помогает лучше понять и прочнее усвоить материал. Свободное владение ситуацией раскрепощает мысль и способствует полёту фантазии.
Рецензенты:Волков В.Я., д.т.н., проф., зав.каф. НГИиКГ ФГОУ ВПО «СибАДИ», г. Омск;
Царёв В.И., д.арх., проф. каф. «Градостроительство» ФГАОУ ВПО СФУ, г. Красноярск.
Библиографическая ссылка
Супрун Л.И., Супрун Е.Г. ОРГАНИЗАЦИЯ ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ СО СТУДЕНТАМИ 1 КУРСА // Современные проблемы науки и образования. 2015. № 4. ;URL: https://science-education.ru/ru/article/view?id=20899 (дата обращения: 11.02.2026).