В последнее десятилетие роевая оптимизация (PSO) нашла применение во множестве областей, таких как социальное моделирование, компьютерная графика, моделирование и анимация природных стада и стаи, распознавание образов, квантование изображения и вычислительная биология.
Оптимизация роя частиц вызвала значительный интерес со стороны компьютерного сообщества. Исследователи постоянно предлагают различные способы улучшения производительности базового метода, которые можно разделить на две группы: комбинационные и метаоптимизационные. Метаоптимизация связана с процессами настройки или управления свободными параметрами роевого алгоритма [1]. Комбинационные методы подразумевают различные способы объединения PSOc другими методами или алгоритмами с целью компенсации недостатков первого за счёт достоинств вторых.
Цель
Целью работы является метаоптимизационная модификация алгоритма роя частиц на основе использования механизмов дробного исчисления с целью улучшения качества его сходимости.
Материалы и методы исследования
Дробное исчисление (Fractional Calculus) является естественным продолжением классической математики. С начала теории дифференциального и интегрального исчисления, несколько математиков исследовали расчет нецелых производных и интегралов. Тем не менее применение дробного исчисления (FC) было малоизвестно до недавнего времени, но последние научные достижения мотивировали повышенный интерес в этой области.
В качестве оптимизационной составляющей классического роевого алгоритма авторы предлагают использовать дробные производные.
Классический алгоритм роя частиц имеет вид:
Существует некая целевая функция f: ℝn → ℝ , которую следует минимизировать. S – число частиц в рое, каждой частице сопоставлена координата 
∈ ℝn в данном пространстве решений и 
∈ ℝn – скорость.
Пусть 
– лучшее из известных положений частицы i, а 
– наилучшее известное состояние роя в целом. Последовательность шагов алгоритма в общем виде выглядит следующим образом:
Для каждой частицы i = 1, …, S:
-
Генерируется начальное положение частицы с помощью случайного вектора.
-
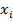рисвоить лучшему известному положению частицы его начальное значение: ← .
-
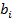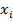Если (f(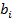) < f(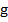)), то обновить наилучшее известное состояние роя: ← .
-
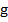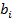Значение скорости частицы:
.
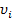Пока не выполнен критерий остановки (например, достижение заданного числа итераций или необходимого значения целевой функции), повторять:
-
Для каждой частицы i = 1, …, S сделать:
-
Обновить скорость частицы: ←
+ 
( -)
.
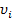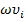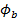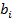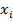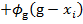где – скорость частицы,
– коэффициент инерции,
когнитивная компонента, которая определяет характеристики частицы относительно ее предыстории,
– социальная компонента, которая характеризует частицу относительно своих соседей,
– лучшее из известных положений частицы i ,
– наилучшее известное состояние роя в целом.
-
Обновить положение частицы переносом 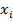на вектор скорости: 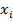← 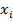+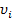. Этот шаг выполняется вне зависимости от улучшения значения целевой функции.
-
Если (f(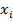) < f(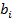)), то:
-
Обновить лучшее известное положение частицы: ← .
-
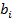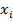Если (f(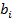) < f(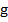)), то обновить лучшее известное состояние роя в целом: ← .
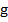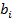Теперь содержит лучшее из найденных решений.
Результаты исследования и их обсуждение
Существует различные способы улучшения классического алгоритма роя частиц:
1. Создание оптимизационного метода, который состоит из соединения нескольких алгоритмов роя частиц.
2. Разовая настройка характеристик движения частиц, посредством которого можно влиять на вероятность преждевременной сходимости.
3. Оптимизация с динамическим изменением параметров алгоритма.
Ограничение скорости – один из методов повышения эффективности PSO. Для данного метода используется уравнение изменения скорости. Это уравнение содержит три слагаемых, которые регулируют величину и направление изменения скорости частицы. В начальных исследованиях было замечено, что скорость частиц может резко увеличиваться, что является характерным для частиц далеких от лучших глобальных и локальных позиций. В итоге частицы выходят за интересующую границу поиска, то есть расходятся. Во избежание таких ситуаций вводится ограничение скорости.
– максимально допустимая скорость в i – й компоненте. Скорость частицы можно регулировать следующим образом:
Данный подход имеет преимущество в том, что сдерживает резкое увеличение скорости [2]. Ограничение скорости влияет не только на шаг изменения, но и на направление движения частицы.
В данной модификации PSO можно отметить такой важный момент:
При удерживании скорости в определенном диапазоне не ограничивается позиция частицы и из этого следует, что изменяется только скорость.
Выбор
определяет скорость сближения частиц. При 
скорость частицы увеличивается и рой «расходится». Частицам трудно менять направление своего движения для возвращения к наиболее лучшей области поиска решения. При <1 частицы будут замедляться, пока их скорость не станет равной нулю. Из этого выходит, что большие значения предназначены для исследования пространства поиска, а малые для локализации решения. Следует учитывать, что очень малые значения не дают рою исследовать пространство поиска. Чем меньше, тем больше влияние когнитивной и социальной компоненты. Как и остальные параметры, оптимальное значение проблемно-ориентировано (индивидуально для каждой задачи) [5].
Обратим внимание на скорость частицы, которая выражена формулой:
← + ( -) (2)
Если рассматривать , как мгновенную скорость неравномерно движущегося тела (в данный момент времени, в данной точке траектории), можно записать:
(3)
Перепишем формулу для скорости частицы в алгоритме при значении = 1:
(4)
Перенесем 
в левую часть, получаем:
Левую часть можно интерпретировать как разностную аппроксимацию первой производной, т.е.
, где T=1 (6)
Подставим (6) в выражение (5):
(7)
Ввиду нелинейности функции 
допускать самоорганизацию, которая обеспечивает достижение общих целей роя на основе низкоуровневого взаимодействия. Из этого можно сделать вывод, о том, что формулам (4) и (5) присуще свойство нелокальности.
Нелокальность – это понятие, которое можно определить как наличие полной информации о всей системе и её элементах в каждой отдельной точке системы, либо как саму возможность того, что любая точка системы может иметь в себе полную информацию о всей системе.
В правой части (6) член, содержащий , можно интерпретировать как память частицы о ее предыдущем состоянии.
Построение схемы, учитывающей информацию о предыдущих значениях координат частиц 
и скоростей 
может способствовать повышению качества оптимизации целевой функции и улучшению сходимости алгоритма роя частиц.
Однако наличие производной 
в (7) в полной мере не позволяет построить нелокальную модель изменения 
, так как не учитывает возможные значения в более ранние моменты, чем t. Выходом из этого состояния является поиск дифференциального оператора, позволяющего учесть приведенное выше обстоятельство.
Отметим также, что в ряде случаев поведению роя при использовании родственных алгоритмов может быть характерна фрактальная динамика [4], выражающаяся в самоподобной конфигурации роя частиц при выполнении поиска оптимума для некоторых нелинейных функций. Ввиду этого искомый оператор должен допускать возможность своего применения в отношении фрактальных объектов.
Вышеперечисленным требованиям удовлетворяет производная нецелого порядка.
Производная нецелого порядка (или производная дробного порядка) является обобщением математического понятия производной.
Производная дробного порядка – это нелокальная характеристика функции:она зависит не только от поведения функции в окрестности рассматриваемой точки x, но и от принимаемых ею значений на всем интервале (
). Изменение плотности потока частиц зависит не только от её значений в окрестности рассматриваемой точки, но и от её значений в удаленных точках пространства. Понятие дробной производной можно интерпретировать в терминах случайных процессов следующим образом. Случайный процесс, скорость изменения плотности которого зависит от значений плотности в предшествующие моменты времени, называется эредитарным. Такие процессы удобно описывать уравнениями, содержащими дробную производную по времени. Порядок производной по времени определяется величиной α.
Для функции
, заданной на отрезке [], каждое из выражений
(8)
(9)
называется дробной производной порядка 
, 0<
соответственно левосторонней и правосторонней. Дробные производные в приведенном виде называют производными Римана – Лиувилля [3].
Альтернативный подход, основанный на определении производной дробного порядка в терминах предельного перехода, основан на ее определении через формулу Грюнвальда –Летникова:
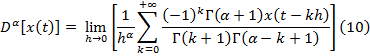
Для численных расчетов можно использовать конечную аппроксимацию (10):
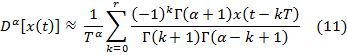
Запишем формулу (7), учитывая выражение (8)-(11):
(12)
Формула (12) позволяет наблюдать учет предыдущих значений 
и так далее.
Аппроксимируя (12) с порядком r=4 и повышая порядок r, получим:
Оценим качество сходимости алгоритма с учетом аппроксимаций (13),(14) и вклад в него параметра . Результат тестирования изображен на рисунке 1. Для тестирования алгоритма была выбрана функция Розенброка:
+
(15)
Тестовая функция рассматривается в диапазоне 
и имеет глобальный минимум равный 0 в точке (1,1).
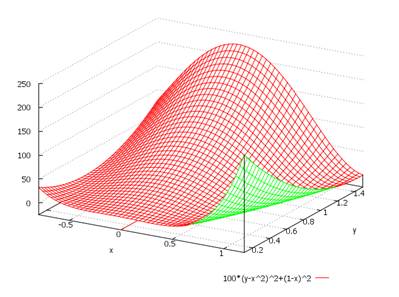
Рис. 1. График функции +
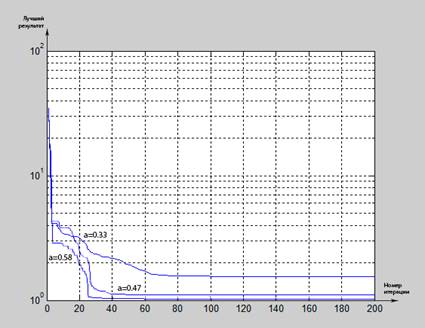
Рис. 2. График зависимости лучшего результата от номера итерации с учетом параметра 
Заключение
FC (дробное исчисление) – хорошо развитый математический инструмент, который позволяет понять, как локальные и глобальные скоростные характеристики влияют на поведение PSO. Понятия FC открывают новые перспективы в направлении разработке более эффективной оптимизации роя.
Предложенный способ метаоптимизации, основанный на дробном исчислении, дает возможность для нахождения оптимального значения скорости движения частиц и позволяет сделать предположение о возможности его расхождения для настройки значения свободных параметров из других известных роевых алгоритмов.
Рецензенты:
Привалов А. Н., д.т.н., профессор Тульского государственного педагогического университета им Л. Н. Толстого, г.Тула;
Петраков В. А., д.т.н., профессор, заведующий кафедрой «Системный анализ и управление» Южного государственного университета, г. Ростов-на-Дону.
Библиографическая ссылка
Дутова И.Г., Мохов В.А., Кузнецова А.В., Есаулов В.А. МЕТАОПТИМИЗАЦИЯ РОЯ ЧАСТИЦ НА ОСНОВЕ МЕТОДА ДРОБНОГО ИСЧИСЛЕНИЯ // Современные проблемы науки и образования. – 2015. – № 2-1. ;URL: https://science-education.ru/ru/article/view?id=20817 (дата обращения: 19.04.2024).