Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

                                                                  (1)

                                                                                                         (2)

где   — фиксированная точка интервала .

Эта задача в более общей постановке изучалась в работе , где были установлены необходимые и достаточные условия ее разрешимости и был разработан численный метод нахождения ее приближенного решения.  Из полученной равномерной оценки погрешности этого решения следует его сходимость к точному решению (1)-(2) со скоростью O(h2), где h – шаг равномерной сетки, на которой строится соответствующая конечно-разностная схема.  Когда принимает положительные значения, может наблюдаться неустойчивость решения дифференциальной задачи (1), (2). Например, это происходит при    и, принимающих близкие значения на отрезке . При условии  погрешность приближенного решения  оказывается величиной порядка ,  где.

Перейдем к изложению численного метода, который при определенных условиях гладкости на коэффициенты уравнения обеспечивает более высокий порядок точности решения.

Введем в рассмотрение функции  и , как решения дифференциальных задач

                                                                   (3)

,                                                                   (4)

соответственно и приведем формулировки теорем, в которых даются необходимые и достаточные условия однозначной разрешимости задачи (1), (2).

Теорема 1. Пусть  ,   и  выполнено условие        

.                                                                                                                                          (5)

Тогда задача  (1), (2) однозначно разрешима, и ее решение представляется в виде        .                                                                                                  (6)

Теорема 2. Пусть  ,   и функция   такова, что для всех    

.                                                                                                                             (7)

Тогда решение задачи (1), (2) существует, единственно и принадлежит классу .

Эти теоремы доказаны в работах, . В дальнейшем будем считать, что выполнены условия  В:,  .           

Имеет место

Теорема 3. Если удовлетворяют условию В и выполнено   (5), то решение задачи (1), (2) принадлежит классу .

Доказательство этой теоремы следует из однозначной разрешимости задач (3) и (4) в классе  при выполнении условий (В), и представления решения в виде (6).

Для численного решения задачи (1),(2) на отрезке введем равномерную сетку   , где шаг сетки   выберем  меньше половины меньшего из отрезков . Номер    выберем из  условия  . Для сеточной функции  введем обозначение  и дифференциальную задачу (3) аппроксимируем конечно-разностной схемой,

,                                                                (8)

,

,

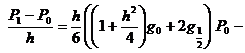
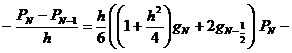
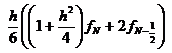где     

,

а дифференциальную задачу (4) — конечно-разностной схемой

              ,                                                   (9)

,

,

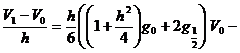
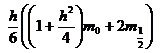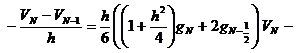
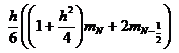где .

С помощью разложений по формуле Тейлора  нетрудно показать, что конечно-разностные схемы (8) и (9) аппроксимируют задачи (3) и (4) соответственно, с точностью  .

Теперь получим аппроксимацию порядка    значения  .  С этой целью через точки,, и  проведем интерполяционный полином Лагранжа третьей степени  :

,                                                        (10)

где коэффициенты Лагранжа вычисляются по формулам:

 ,   ,

,   .                                   (11)

Величину  примем за приближенное значение  и оценим погрешность такой аппроксимации. Для этого проведем интерполяционный полином Лагранжа через точки ,, и   . Он имеет вид:        

,                                                       (12)

где коэффициенты Лагранжа  вычисляются по формулам (11). Так как функция  имеет четвертую производную на отрезке , то, воспользовавшись, известной оценкой погрешности формулы Лагранжа  ,  получаем оценку:

.                                                                                              (13)     Так как , то разность      является величиной             . Следовательно, найдется положительная постоянная             такая, что:                                           .                                                                                                       (14)                 По аналогии с аппроксимацией  , значение   аппроксимируем величиной  , равной значению в           точке  интерполяционного полинома Лагранжа, проведенного через точки            ,, и   , т.е.                                                                        .                                            (15)

Очевидно, найдется положительная постоянная               , такая, что:                   

.                                                                                                            (16)

            В качестве приближенного решения задачи (1), (2) выберем сеточную функцию

, .                                                                                              (17)

Имеет место

Теорема  4. Пусть  выполнены условия В и (5).  Тогда сеточная функция ,  определенная по формуле (17), сходится при    к  решению  задачи (1), (2) со скоростью    в равномерной метрике.

            Доказательство. Пользуясь представлением (6) точного решения , получаем   оценку погрешности    в равномерной метрике:

.                                                                                         (18)

Оценим слагаемые в правой части (18). Поскольку конечно-разностные схемы (8) и (9) сходятся к решениям дифференциальных задач (3) и (4) с порядком  соответственно, то найдутся положительные постоянные  и   не зависящие от , что:

,   .                                                                                (19)

Условие  означает, что либо  ,  либо .  Введем обозначение  .  Оценим теперь снизу .  Из (14) следует, что при     имеет место оценка  , откуда получаем:

.                                                                             (20)

Пусть .  Воспользовавшись оценкой  , полученной в  ,    из левой части (20) получаем:   .

Пусть . Так как в этом случае  , то из правой части (20) следует оценка . Таким образом, найдется , что при  имеет место оценка:

.                                                                                                                       (21)

Решение  задачи (3) и решение задачи (9) оцениваются соответственно в виде:

,  .                                                                                       (22)

Применяя оценки (15), (16), (19), (21), (22) из (18), получаем:

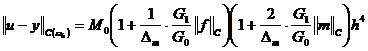,                                                   (23)

где . 

         Из (23) следует утверждение теоремы 4.

При  может наблюдаться неустойчивость решения задачи (1), (2).  В частности,  если  близко к  во всех точках  настолько, что , где , то предложенный алгоритм позволяет вычислить  решение   задачи (1), (2) с точностью .

Шхануков-Лафишев М.Х, д.ф.-м.н., профессор, ФГБУН «Институт информатики и проблем регионального управления   Кабардино-Балкарского   научного центра РАН», г. Нальчик.

Ашабоков Б.А., д.ф.-м.н., профессор Высокогорного Геофизического Института, г. Нальчик.