Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Мысль И.Бернулли о том, что "природа всегда действует простейшим образом", т.е. "наиболее экономно", чрезвычайно стара и послужила источником многих научных идей и методических приемов. Сошлемся еще раз на И.Ньютона, который в своих "Началах" говорит: "Не должно принимать в при­роде иных причин сверх тех, которые истинны и достаточны для объяснения яв­лений. Природа ничего не делает напрасно, а было бы напрасным совершать мно­гим то, что может быть сделано меньшим. Природа проста и не раскошеству­ет  излишними причинами вещей". Эта мысль была источником не только методо­логии Ньютона, но и чисто физической идеи о равенстве тя-желой и инертной масс- идеи, имевшей столь далекие последствия в общей теории относительности. Вскоре в физике и математике идея "экономии" получила воплощение в экстре­мальных (вариационных) принципах.

 В 1696 году И. Бернулли, пользуясь принципом Ферма, показал, что траек­тория наискорейшего спуска тела, движущегося в вертикальной плоскости под действием силы тяжести, точно такая же, как траектория светового луча, распро­страняющегося в среде с возрастающей или убывающей по определенному закону плотности. (Впервые аналогию между движением света и брошенного тела рассмотрел знаменитый арабский оптик ХI века Ибн аль-Хайсам). Так возник новый метод сопоставления оптических и механических величин_ оптико-механическая аналогия. 

Следуя идее Гельмгольца_ "понять какой-либо процесс в природе_ это значит перевести его на язык механики", выбрав механическую аналогию в описании оптических явлений, приходим к принципу Ферма наимень­шего времени (1662 г.) при изучении геометрической оптики. Вся геометрическая оптика заключена в этом принципе и может быть получена из него путем методического развер­тывания с учетом конкретных условий распространения света. Используя принцип Ферма (свет распространяется по экстремальному опти­ческому пути), можно получить закон прямолинейного распространения света в однородной среде, так как в однородной среде кратчайшим оптическим путем является прямая линия.

Однако в неоднородной среде (переменный показатель преломления) крат­чайшим оптическим путем может оказаться кривая (или ломаная) линия, вдоль которой показатель преломления меньше, чем вдоль геометрической прямой. Этим объясняется явление преломления света и явление рефракции_ искривление световых лучей в неоднородной среде.

Еще Герон Александрийский выводил закон отражения света из принципа кратчайшего пути. Однако уже в случае преломления света этот принцип явно на­рушался. Поэтому П. Ферма предположил, что световой луч избирает не кратчай­ший путь, а путь наименьшего времени. Так был сформулирован первый вариа­ционный принцип в физике. Согласно принципу Ферма, свет распространяется между двумя точками  по такому пути, который тре­бует для прохождения наименьшего времени [2].

Цель исследования. Обсуждение проблемы формирования методологических знаний в рамках метаметодической модели обучения при изучении методов аналогии и оптимизации. Развитие компетентностного подхода в частной методике на основе дидактических функций задач в плане формирования профессиональных и общекультурных компетенций. 

Методы исследования. В работе применялись общетеоретические и экспериментальные методы педагогических исследований. Проектирование метаметодической системы обучения физике носит межпредметный характер. В связи с этим решалась проблема актуализация физических знаний в учебном процессе, апробация результатов педагогических исследований осуществлялась на международных и всероссийских научно-практических конференциях проводимых в СПбГИКиТ.

Результаты исследования и их обсуждение

Оптическую задачу о преломлении света можно сформулировать как задачу нелинейного программирования, например, в интегрированной среде Maple. При наличии нескольких границ раздела сред (например, воздух-вода-глицерин) с помощью стандартных функций пакета оптимизации рассчитывается ход лучей.

> restart:with(Optimization):

L:= n[1]*sqrt(a^2+x[1]^2)+sum(n[k+1]*sqrt(b^2+(x[k+1]-x[k])^2),k=1..N-1);

a:=0.5: b:=0.01: c:=10:

N:=7: n[1]:=1; n[2]:=1.3; dn:=0.02:

for i from 2 to N-1 do

n[i+1]:=n[i]+dn od; x[N]:=c:  NLPSolve(n[1]*sqrt(a^2+x[1]^2)+sum(n[k+1]*sqrt(b^2+(x[k+1]-x[k])^2),k=1..N-1),{seq(x[k]<=c,k=1..N-1)}, assume = nonnegative);

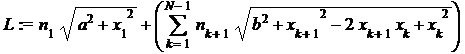
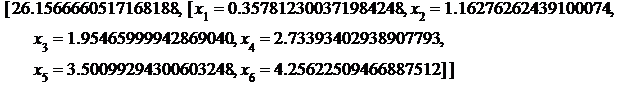
Программирование с функциями символьных преобразований в циклическом алгоритме позволяет разработать компьютерную модель физического эксперимента.

Постановка задачи оптимизации_ это, прежде всего четкая формулировка целевой функции и установление системы ограничений. Целевая функция представляет собой критерий отбора среди всех возможных планов задачи одного оптимального. Как правило, в роли ограничений выступают ресурсы системы. Таким образом, задачи математического программирования формулируются следующим образом: найти экстремальное значение целевой функции       при условиях (ограничениях)  , где i=1...m.  В компактном виде данная задача записывается так:

, причем, М- заданная ограничениями область изменения переменных "х".

При этом не оговаривается ни форма целевой функции, ни вид неравенств задающих ограничения. В общем случае, задачи относятся к нелинейному программированию. Наличие особенностей, связанных с нелинейностью, существенно усложняет решение задач математического программирования. Имеется целый ряд частных методов, каждый из которых приспособлен к решению задач определенного типа  [1].

В отдельных случаях могут быть линейными как целевая функция, так и функции ограничения- это задачи линейного программирования, которые могут быть исследованы симплекс-методом, графическим методом или методом потенциалов. Кроме того, существуют пакеты прикладных компьютерных программ (например, Maple), реализующие основные алгоритмы решения задач математического программирования.

Знакомство с методами оптимизации возможно при рассмотрении баллистической задачи (задача нелинейного программирования). В отсутствии сопротивления среды траектория напоминает контур луча в неоднородной среде с переменным показателем преломления. Достаточно в плоскости задать целевую функцию координат, например, радиус-вектор или потенциальную энергию и затем воспользоваться возможностями математического пакета Maple.

> a:=(Pi/4):v0:=10: g:=10: m:=1: NLPSolve(sqrt(x^2+y^2),{y-(x*tan(a)-(g*x^2)*(1+tan(a)^2)/(2*v0^2))=0}, assume = nonnegative,maximize);S:=v0^2/g;

 

> a:=(Pi/4):v0:=10: g:=10: m:=1: NLPSolve(m*g*y,{y-(x*tan(a)-(g*x^2)*(1+tan(a)^2)/(2*v0^2))=0}, assume = nonnegative,maximize);S:=(v0)^2/g; h:=(v0*sin(a))^2/(2*g); U:=m*g*h;

 

             Многие задачи, например, в экономике сводятся к линейным математическим моделям. Традиционно оптимизационные линейные математические модели называются моделями линейного программирования. Под линейным программированием понимается линейное планирование, то есть получение оптимального плана. 

           В широком смысле, линейное программирование – область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума и минимума) линейной функции многих переменных при наличии линейных ограничений, то есть линейных равенств или неравенств, связывающих эти переменные. К задачам линейного программирования сводится широкий круг вопросов планирования экономических процессов, где ставится задача поиска наилучшего (оптимального) решения  [4]. 

           Линейное программирование - новая область прикладной математики. Основные идеи линейного программирования были развиты всего лишь три десятилетия назад. В 1939 г. появилась работа советского академика Л. В. Канторовича «Математические методы в организации и планировании производства». В 1949 г. опубликована работа американского математика Джорджа Б. Данцига, в которой излагались идеи метода последовательного улучшения плана, называемого теперь симплексным методом. Этот метод является одним из самых универсальных и эффективных [3].

            Наиболее простым и наглядным методом решения задачи линейного программирования является графический метод. Он основан на геометрической интерпретации задачи линейного программирования. Пример графического метода можно рассмотреть на рис.1, где было построено 3 прямые линии, а решением является многогранная область ABCDF. Геометрически задача линейного программирования представляет собой отыскание такой угловой точки многоугольника решений, координаты которой доставляют максимальное (или минимальное) значение линейной целевой функции, причем допустимыми решениями являются все точки многоугольника решений  [6]. 

              Из чертежа всегда видно, разрешима задача или нет. Из чертежа также видно, имеются ли у допустимого множества X вершины. При использовании графического метода можно избежать полного перебора вершин. Действительно, если из чертежа видно, что А – единственная первая (или последняя) точка пересечения линии уровня с X, то не нужно вычислять координаты других вершин, так как А – единственное оптимальное решение. В некоторых случаях из чертежа не ясно, в какой именно точке линия уровня пересекает в первый раз допустимое множество X. В этом случае нужно найти координаты всех похожих на оптимальность вершин, вычислить для указанных вершин их значения целевой функции и выбрать из них вершины с оптимальным значением.

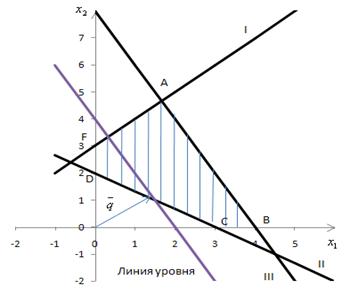
Рис. 1  Иллюстрация графического метода линейного программирования

                Решение основной задачи линейного программирования графическим методом является наглядным в случае двух и даже трех переменных. Для случая большого числа переменных геометрический метод становится невозможным и тогда используется симплекс-метод, где используется тот факт, что если задача линейного программирования имеет решение, то хотя бы одно из них – угловая точка (базисное). 

          Для упрощения процесса решения исходные данные задачи линейного программирования при решении ее симплекс методом записываются в специальные симплекс-таблицы. Поэтому одна из модификаций симплекс метода получила название табличный симплекс метод [6].

          Выводы

В системе современных знаний физика продолжает формировать стиль на­учного мышления, задает его нормы, т. е. остается лидером современного естест­вознания. Овладение основами физического мышления должно осу­ществляться на разных уровнях обучения. Речь идет о вооружении учащихся знанием истории и методологии науки, сознательного использования интеллектуальных умений.  

         Изучая задачи оптимизации, универсальность методов математического моделирования уместно вспомнить А. Пуанкаре, - «все законы выводятся из опыта. Но для их выражения нужен специальный язык. Обиходный язык слишком беден, кроме того, он слишком неопределенен для выражения столь богатых содержанием точных и тонких соотношений. Таково первое основание, по которому физик не может обойтись без математики; она дает ему единственный язык, на котором он в состоянии изъясняться». Чтобы вывести закон из опыта, необходимо обобщать. Какими критериями следует руководствоваться при проведении этих обобщений? Как отмечает А. Пуанкаре, - «руководителем может быть только аналогия… Но кто же научил нас познанию истинных, глубоких аналогий, таких, которые не видит глаз, но которые отгадывает разум? Этому научил нас математический ум, который пренебрегает содержанием, чтобы иметь дело только с чистой формой. Это он научил нас называть одним и тем же именем все сущности, отличающиеся только своим содержанием» [5].

Рецензенты:

Ларченкова Л.А., д.п.н., доцент, доцент кафедры методики обучения физике ФГБОУ «Российский государственный педагогический университет им. А.И.Герцена» Министерство образования и науки РФ, г. Санкт-Петербург;

Смирнов Н.В., д.ф.-м.н., доцент, профессор кафедры моделирования экономических систем факультета прикладной математики- процессов управления Санкт-Петербургского государственного университета Министерство образования и науки РФ, г. Санкт-Петербург.